[HNOI2013]切糕（最小割最大流）

题目：洛谷P3227、LOJ#2384

题目描述：

有一个三维立体点阵\((i,j,k)\)，其中\(1\leq i \leq P\),\(1 \leq j \leq Q\),\(1 \leq k \leq R\)，每个点都有一个价值，在每一个纵轴\((i,j)\)上选一个点，相邻两个纵轴上的选的点的高度差不能超过\(D\)，求选中的点集的价值之和的最小值

\(P, Q, R \leq 40\),\(D < R\)
任意点的价值不超过\(1000\)

蒟蒻题解：

把点看成边的话，每个纵轴上选择一条边，把这个纵轴割成上下两段，让最上方和最下方不连通，且要让割的代价最小

这有点像网络流最小割

在最上方建源点\(S\)，在最下方建汇点\(T\)，记第\((i,j)\)个纵轴上第\(k\)层的坐标为\((i,j,k)\)，记第\((i,j,k)\)上的价值为\(val(i,j,k)\)

如果一个纵轴只割一条边的话，要让相邻纵轴上割的边的高度差不能超过\(D\)，可以等价为限制相邻纵轴上割的边的高度不能超过当前纵轴割的边的高度\(-D\)，对于相邻两个纵轴，相互限制，即可达到目的

连边：
\(S\)->\((i,j,1)\)，连流量为\(val(i,j,1)\)的边
\((i,j,k-1)\)->\((i,j,k)(1 < k \leq R)\)，连流量为\(val(i,j,k)\)的边
\((i,j,R)\)->\(T\)，连流量为\(INF\)的边
\((i,j,k)\)->\((i',j',k-D)(|i-i'|+|j-j'|=1)\)，连流量为\(INF\)的边

但是会不会出现一个纵轴割了多条边的情况呢？

对于最小割中会割掉的边，一定满足\(S\)->左端点，右端点->\(T\)，这样不割的话会使得\(S\)->\(T\)联通，所以要割掉，否则不割掉更优就不会割掉

假设一个纵轴有多条割边，对于每个纵轴，\(S\)刚开始只和当前纵轴第一条割边左侧相连，所以一定存在某个纵轴第一条割边和第二条割边之间的链可以通过另一个纵轴第一条割边左侧的链到达

如图

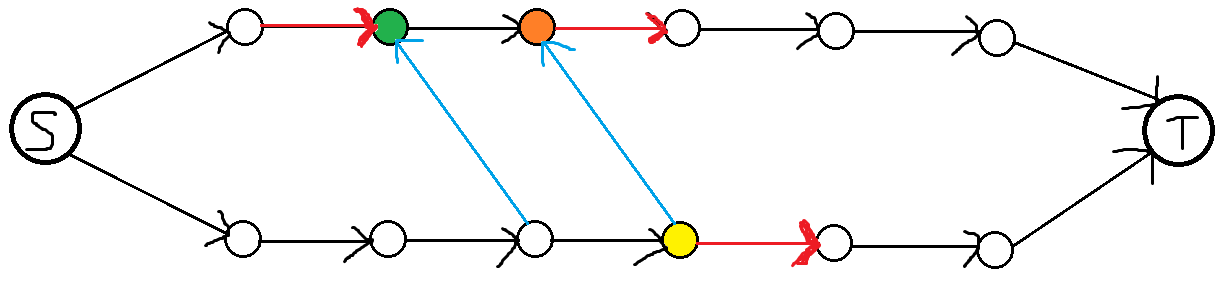
红色的边表示割边，绿点表示某个纵轴第一条割边与第二条割边之间链的第一个点，橙点表示某个纵轴第一条割边与第二条割边之间链的最后一个点，黄点表示连向橙点的点

由于第一条割边与第二条割边需要割，所以满足\(S\)能到达橙点，绿点能到达\(T\)，由于黄点在下方的第一条割边之前，黄点->橙点，所以肯定存在点指向绿点，即\(S\)能到达绿点，又绿点能到达\(T\)，即存在\(S\)到达\(T\)的路径，与最小割存在矛盾

故不会出现一个纵轴割了多条边的情况

参考程序：

#include<bits/stdc++.h>
using namespace std;
#define Re register int

const int N = 64005, M = 768005, Inf = 1e9;
int P, Q, R, D, num, t, cnt = 1, l, r, ans, id[45][45][45], hea[N], h[N], d[N], q[N], nxt[M], to[M], wi[M];

inline int read()
{
	char c = getchar();
	int ans = 0;
	while (c < 48 || c > 57) c = getchar();
	while (c >= 48 && c <= 57) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
	return ans;
}

inline void add(int x, int y, int z)
{
	nxt[++cnt] = hea[x], to[cnt] = y, wi[cnt] = z, hea[x] = cnt;
	nxt[++cnt] = hea[y], to[cnt] = x, hea[y] = cnt;
}

inline bool bfs()
{
	for (Re i = 0; i <= t; ++i) h[i] = hea[i], d[i] = 0;
	d[l = r = 0] = 1;
	while (l <= r)
	{
		int x = q[l++];
		for (Re i = hea[x]; i; i = nxt[i])
		{
			int u = to[i];
			if (!wi[i] || d[u]) continue;
			d[q[++r] = u] = d[x] + 1;
			if (u == t) return 1;
		}
	}
	return 0;
}

inline int dinic(int x, int y)
{
	if (x == t) return y;
	int res = y;
	for (Re &i = h[x]; i; i = nxt[i])
	{
		int u = to[i];
		if (!wi[i] || d[u] ^ d[x] + 1) continue;
		int v = dinic(u, min(res, wi[i]));
		if (v)
		{
			wi[i] -= v, wi[i ^ 1] += v, res -= v;
			if (!res) break;
		}
	}
	return y - res;
}

int main()
{
	P = read(), Q = read(), R = read(), D = read(), t = P * Q * R + 1;
	for (Re i = 1; i <= R; ++i)
		for (Re j = 1; j <= P; ++j)
			for (Re k = 1; k <= Q; ++k)
			{
				add(id[i - 1][j][k], id[i][j][k] = ++num, read());
				if (i == R) add(id[i][j][k], t, Inf);
				if (i > D)
				{
					if (j > 1) add(id[i][j][k], id[i - D][j - 1][k], Inf);
					if (j < P) add(id[i][j][k], id[i - D][j + 1][k], Inf);
					if (k > 1) add(id[i][j][k], id[i - D ][j][k - 1], Inf);
					if (k < Q) add(id[i][j][k], id[i - D][j][k + 1], Inf);
				}
			}
	int fl;
	while (bfs())
		while (fl = dinic(0, Inf)) ans += fl;
	printf("%d", ans);
	return 0;
}