统一省选简要题解
Day1
[省选联考 2021 A/B 卷] 卡牌游戏
洛谷P7514、LOJ#3499
有\(n\)张卡牌,第\(i\)张卡牌正面的数字为\(a_i\),背面的数字为\(b_i\),初始均为正面朝上,让不超过\(m\)张卡牌翻面,要让这\(i\)张卡牌朝上的数字组成序列的极差最小,求出这个最小值
保证\(a_i\)递增
\(3 \leq n \leq 10^6\),\(1 \leq m < n\),\(1 \leq a_i,b_i \leq 10^9\)
将某些\(a_i\)翻面,使其变成\(b_i\),一定是将前面一段\(a_i\)和后面一段\(a_i\)翻面,中间不需要翻面,假设\(a_l\)与\(a_r\)没被翻面,那么对于任意\(a_i(l < i < r)\),由于\(a_l < a_i < a_r\),所以\(a_i\)不可能是最大值,也不可能是最小值,所以将\(a_i\)翻面不可能使答案变优
假设将\(a_1 \sim a_{l-1}\)和\(a_{r+1} \sim a_n\)翻面,要让\(a_{l-1}\)翻面有意义,所以需要满足\(min(b_1,b_2,...b_{l-1})>a_{l-1}\)且\(min(b_{r+1},b_{r+2},...b_n)>a_{l-1}\),要让\(a_{r+1}\)翻面有意义,所以需要满足\(max(b_1,b_2,...b_{l-1})<a_{r+1}\)且\(max(b_{r+1},b_{r+2},...b_{n})<a_{r+1}\)
当\(l,r\)固定住时,当前最大值即为\(max(max(b_1,b_2,...b_{l-1}),max(b_{r+1},b_{r+2},...b_{n}),a_r)\),将其记为\(Max\),当前最小值即为\(min(min(b_1,b_2,...b_{l-1}),min(b_{r+1},b_{r+2},...b_n),a_l)\),将其记为\(Min(Min \in (a_{l-1}, a_l])\),当前的极差记为\(Max-Min\)
当我们将\(r\)固定时,如果\(max(b_1,b_2,...b_{l-1})<a_r\),当\(l\)减小时,\(max(b_1,b_2,...b_{l-1})\)不增,由\(Max=max(max(b_1,b_2,...b_{l-1}),max(b_{r+1},b_{r+2},...b_{n}),a_r)\)可知\(Max\)不变,由\(Min=min(min(b_1,b_2,...b_{l-1}),min(b_{r+1},b_{r+2},...b_n),a_l)\)且\(min(b_1,b_2,...b_{l-1})>a_{l-1}\)且\(min(b_{r+1},b_{r+2},...b_n)>a_{l-1}\)可知\(Min\)减小,极差\(Max-Min\)会变大,所以当\(max(b_1,b_2,...b_{l-1})<a_r\)时,\(l\)减小肯定更不优,不需要减小,又\(max(b_1,b_2,...b_{l-1})<a_{r+1}\),令\(l\)取到的最小的值为\(x\),\(l\)取到的最大的值为\(y\),\(x\)为最大的满足\(max(b_1,b_2,...b_{l-1})<a_r\)的\(l\),\(y\)为最大的满足\(max(b_1,b_2,...b_{l-1})<a_{r-1}\)的\(l\),\(l \in [x,y]\),对于相邻的\(r\)他们所对应的\(l\)均为连续的区间,且仅有一个点重合,且除去重合的点,区间在向左移,具有单调性
从大到小枚举每一个\(r\),\(l\)也随之递减,时间复杂度为\(\mathcal O(n)\)
#include<bits/stdc++.h>
using namespace std;
#define Re register int
const int N = 1000005, Inf = 1e9 + 5;
int n, m, l, ans, a[N], b[N], mn[N], mx[N];
inline int read()
{
char c = getchar();
int ans = 0;
while (c < 48 || c > 57) c = getchar();
while (c >= 48 && c <= 57) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
return ans;
}
inline int max(int x, int y)
{
return x > y ? x : y;
}
inline int min(int x, int y)
{
return x < y ? x : y;
}
int main()
{
n = read(), m = read(), mn[0] = a[n + 1] = ans = Inf;
for (Re i = 1; i <= n; ++i) a[i] = read();
for (Re i = 1; i <= n; ++i) b[i] = read(), mx[i] = max(b[i], mx[i - 1]), mn[i] = min(b[i], mn[i - 1]);
while (l < m && mn[l + 1] > a[l + 1]) ++l;
for (Re i = n + 1, mxx = 0, mnn = Inf; i > n - m; --i, mxx = max(mxx, b[i]), mnn = min(mnn, b[i]))
{
if (mxx >= a[i]) break;
if (l + n + 1 - i > m) --l;
while(mx[l] >= a[i - 1]) ans = min(ans, max(mx[l], mxx) - min(min(mn[l], a[l + 1]), mnn)), --l;
ans = min(ans, max(a[i - 1], mxx) - min(min(mn[l], a[l + 1]), mnn));
}
printf("%d", ans);
return 0;
}
[省选联考 2021 A 卷] 矩阵游戏
对于每组数据给了一个\((n-1) \times (m-1)\)的矩阵\(b_{i,j}\)满足\(b_{i,j} = a_{i,j} + a_{i,j+1} + a_{i+1,j} + a_{i+1,j+1}\),要求还原出一个\(n \times m\)的矩阵\(a_{i,j}\),对于任意\(a_{i,j}\)需要满足\(0 \leq a_{i,j} \leq 10^6\)
\(1 \leq T \leq 10\),\(2 \leq n,m \leq 300\),\(0 \leq b_{i,j} \leq 4 \times 10^6\)
将矩阵\(a_{i,j}\)第一行与第一列固定住后,可以确定唯一一种满足\(b_{i,j}=a_{i,j}+a_{i,j+1}+a_{i+1,j}+a_{i+1,j+1}\),但不一定满足\(0 \leq a_{i,j} \leq 10^6\)的方案
考虑随便构造出一个满足\(b_{i,j}=a_{i,j}+a_{i,j+1}+a_{i+1,j}+a_{i+1,j+1}\)的矩阵\(A_{i,j}\),经过一些调整得到合法的方案
发现对于一行来说,执行+1,-1,+1,-1...,还是一种满足\(b_{i,j}=a_{i,j}+a_{i,j+1}+a_{i+1,j}+a_{i+1,j+1}\)的方案,如下图所示操作
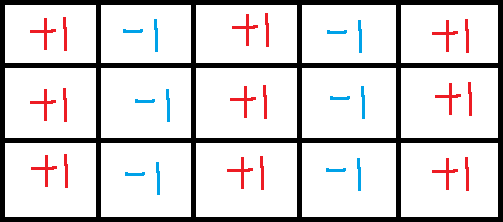
对于一列同理
假设对于第\(i\)行执行\(r_i\)次操作,第\(i\)列执行\(c_i\)次操作,通过这样的操作,可以表示出所有的第一行和第一列,即可以表示出所有满足\(b_{i,j}=a_{i,j}+a_{i,j+1}+a_{i+1,j}+a_{i+1,j+1}\)的方案
对于格子\((i,j)\),如果\(i\)为奇数,它会增加\(c_j\),否则它会减少\(c_j\),如果\(j\)为奇数,它会增加\(r_i\),否则它会减少\(r_i\)
发现每个格子增加的值有\(4\)种情况:\(r_i+c_j\)、\(r_i-c_j\)、\(-r_i+c_j\)、\(-r_i-c_j\),发现这样很难处理,如果只有减的话就可以进行差分约束来解决,尝试能不能把它换成只有减的情况
为了让每个格子的\(r_i\)和\(c_j\)的正负性相反,可以改变一下,把奇数行和偶数列的操作取反,改成-1,+1,-1,+1...
这样对于格子\((i,j)\),如果\(i、j\)奇偶性相同,那么会增加\(c_j-r_i\),如果奇偶性不同则会增加\(r_i-c_j\),记这个增加的值为\(B_{i,j}\),则\(a_{i,j}=A_{i,j}+B_{i,j}\),又\(0 \leq a_{i,j} \leq 10^6\),\(A_{i,j}\)为之前构造出来的,\(B_{i,j}\)为两个未知变量的差值,那么可以通过差分约束来构造出一组合法的解
最坏复杂度是\(\mathcal O(T(n+m)nm)\),但是远远跑不满
#include<bits/stdc++.h>
using namespace std;
#define Re register int
typedef long long ll;
const int N = 305, M = 605, K = 180005;
int T, n, m, cnt, a[N][N], b[N][N], res[M], hea[M], nxt[K], to[K], len[K];
bool p, vis[M];
ll dis[M];
deque<int> q;
inline int read()
{
char c = getchar();
int ans = 0;
while (c < 48 || c > 57) c = getchar();
while (c >= 48 && c <= 57) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
return ans;
}
inline void write(int x)
{
int num = 0;
char sc[15];
if (!x) sc[num = 1] = 48;
while (x) sc[++num] = x % 10 + 48, x /= 10;
while (num) putchar(sc[num--]);
putchar(' ');
}
inline void add(int x, int y, int z)
{
nxt[++cnt] = hea[x], to[cnt] = y, len[cnt] = z, hea[x] = cnt;
}
int main()
{
T = read();
while (T--)
{
n = read(), m = read(), cnt = p = 0;
while (!q.empty()) q.pop_back();
for (Re i = 1; i <= n + m; ++i) hea[i] = dis[i] = 0, res[i] = vis[i] = 1, q.push_back(i);
for (Re i = 1; i < n; ++i)
for (Re j = 1; j < m; ++j) b[i][j] = read();
for (Re i = 1; i <= n; ++i) a[i][1] = 0;
for (Re i = 2; i <= m; ++i) a[1][i] = 0;
for (Re i = 2; i <= n; ++i)
for (Re j = 2; j <= m; ++j) a[i][j] = b[i - 1][j - 1] - a[i - 1][j - 1] - a[i - 1][j] - a[i][j - 1];
for (Re i = 1; i <= n; ++i)
for (Re j = 1; j <= m; ++j)
if ((i ^ j) & 1) add(n + j, i, 1000000 - a[i][j]), add(i, n + j, a[i][j]);
else add(i, n + j, 1000000 - a[i][j]), add(n + j, i, a[i][j]);
while (!q.empty())
{
int x = q.front();
q.pop_front();
vis[x] = 0;
for (Re i = hea[x]; i; i = nxt[i])
{
int u = to[i];
if (dis[u] <= dis[x] + len[i]) continue;
dis[u] = dis[x] + len[i], res[u] = res[x] + 1;
if (res[u] > n + m)
{
p = 1;
puts("NO");
break;
}
if (!vis[u])
{
vis[u] = 1;
if (!q.empty() && dis[u] < dis[q.front()]) q.push_front(u);
else q.push_back(u);
}
}
if (p) break;
}
if (p) continue;
puts("YES");
for (Re i = 1; i <= n; ++i)
{
for (Re j = 1; j <= m; ++j)
{
if ((i ^ j) & 1) a[i][j] += dis[i] - dis[n + j];
else a[i][j] += dis[n + j] - dis[i];
write(a[i][j]);
}
putchar('\n');
}
}
return 0;
}
[省选联考 2021 A/B 卷] 图函数
洛谷P7516、LOJ#3501
对于一张\(n\)个点\(m\)条边的有向图\(G\)(顶点从\(1 \sim n\)编号),定义函数\(f(u, G):\)
-
初始化返回值\(cnt=0\),图\(G'=G\)
-
从\(1\)至\(n\)按顺序枚举顶点\(v\),如果当前的图\(G'\)中,从\(u\)到\(v\)与从\(v\)到\(u\)的路径都存在,则将\(cnt+1\),并在图\(G'\)中删去顶点\(v\)以及与它相关的边
-
第\(2\)步结束后,返回值\(cnt\)即为函数值
现在给定一张有向图\(G\),请你求出\(h(G)=f(1,G)+f(2,G)+ \cdots +f(n,G)\)的值
记删除(按输入顺序给出的)第\(1\)到\(i\)条边后的图为\(G_i(1 \leq i \leq m)\),请求出所有\(h(G_i)\)的值
\(2 \leq n \leq 10^3\),\(1 \leq m \leq 2 \times 10^5\),\(1 \leq x_i,y_i \leq n\)
考虑计算\(f(u,G)\),对于一个点\(x\),如果会使\(cnt+1\),当且仅当\(x\)到\(u\)和\(u\)到\(x\)上的所有的点均\(\geq x\),假设存在一个点\(y<x\),且\(y\)存在于\(x\)到\(u\)的路径或\(u\)到\(x\)的路径上,那么\(y\)一定会在之前就被删掉
考虑计算\(h(G)\),对于点对\((x,y)(x<y)\),存在\(x\)到\(y\)的路径和\(y\)到\(x\)的路径,路径仅能由两个端点均\(\geq x\)的的边组成,那么答案就会\(+1\)
由于它每次删掉一个前缀的边,逆着来相当于每次加一条边进去,对于点对\((x,y)(x<y)\),记存在\(x\)到\(y\)的路径和\(y\)到\(x\)的路径,路径仅能由两个端点均\(\geq x\)的的边组成,路径上所有边的最小值最大为\(z\),那么对于\(h(G),h(G_1),h(G_2),...h(G_{z-1})\),它均会产生贡献
法一:
对于点对\((x,y)(x<y)\)产生贡献,它只能由两个端点都\(\geq x\)的边组成,可以\(Floyd\),中间转折点为\(\geq x\)的点,转折点从大到小,求\(dis_{i,j}\)表示\(i\)到\(j\)经过的边的最小边最大为多少,对于点对\((x,y)\),会对在\(min(dis_{x,y},dis_{y,x})\)之前的图产生贡献,差分一下,总的时间复杂度为\(\mathcal O(n^3+m)\)
法二:
对于点对\((x,y)(x<y)\),可以枚举点\(x\),反向加边,且只保留\(\geq x\)的点,看\(x\)到\(y\)所需要的最小边最大是多少,直接\(bfs/dfs\)即可,然后再用反向边跑一遍,\(y\)到\(x\)的路径就是将所有边反向后\(x\)到\(y\)的路径,由于边是从大到小加,要求所需要的最小边最大是多少,所以每个点只需要经过一次即可,时间复杂度\(\mathcal O(n(m+n))\)
以下为法一的代码
#include<bits/stdc++.h>
using namespace std;
#define Re register int
const int N = 1005;
int n, m, ans[200005], f[N][N];
inline int read()
{
char c = getchar();
int ans = 0;
while (c < 48 || c > 57) c = getchar();
while (c >= 48 && c <= 57) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
return ans;
}
inline void write(int x)
{
int num = 0;
char sc[15];
while (x) sc[++num] = x % 10 + 48, x /= 10;
while (num) putchar(sc[num--]);
putchar(' ');
}
inline int min(int x, int y)
{
return x < y ? x : y;
}
inline int max(int x, int y)
{
return x > y ? x : y;
}
int main()
{
n = read(), m = read();
for (Re i = 1; i <= m; ++i)
{
int u = read(), v = read();
f[u][v] = i;
}
for (Re i = 1; i <= n; ++i) f[i][i] = m + 1;
for (Re i = n; i; --i)
{
for (Re j = 1; j < i; ++j)
{
if (!f[j][i]) continue;
for (Re k = j + 1; k <= n; ++k)
if (k ^ i) f[j][k] = max(f[j][k], min(f[j][i], f[i][k]));
}
for (Re j = 1; j < i; ++j)
{
if (!f[i][j]) continue;
for (Re k = j + 1; k <= n; ++k)
if (k ^ i) f[k][j] = max(f[k][j], min(f[k][i], f[i][j]));
}
}
for (Re i = 1; i <= n; ++i)
for (Re j = i; j <= n; ++j) ++ans[min(f[i][j], f[j][i])];
for (Re i = m; i; --i) ans[i] += ans[i + 1];
for (Re i = 1; i <= m + 1; ++i) write(ans[i]);
return 0;
}
以下为法二的代码
#include<bits/stdc++.h>
using namespace std;
#define Re register int
const int N = 1005, M = 200005;
struct info
{
int l, r;
}a[M];
int n, m, cnt, f[N], g[N], ans[M], hea[N], nxt[M], to[M];
inline int read()
{
char c = getchar();
int ans = 0;
while (c < 48 || c > 57) c = getchar();
while (c >= 48 && c <= 57) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
return ans;
}
inline void write(int x)
{
int num = 0;
char sc[15];
while (x) sc[++num] = x % 10 + 48, x /= 10;
while (num) putchar(sc[num--]);
putchar(' ');
}
inline int min(int x, int y)
{
return x < y ? x : y;
}
inline void add(int x, int y)
{
nxt[++cnt] = hea[x], to[cnt] = y, hea[x] = cnt;
}
inline void dfs(int x, int y)
{
f[x] = y;
for (Re i = hea[x]; i; i = nxt[i])
{
int u = to[i];
if (!f[u]) dfs(u, y);
}
}
int main()
{
n = read(), m = read();
for (Re i = 1; i <= m; ++i) a[i].l = read(), a[i].r = read();
for (Re i = 1; i <= n; ++i)
{
for (Re j = i; j <= n; ++j) hea[j] = f[j] = 0;
cnt = 0, f[i] = m + 1;
for (Re j = m; j; --j)
{
int u = a[j].l, v = a[j].r;
if (f[v] || u < i || v < i) continue;
add(u, v);
if (f[u]) dfs(v, j);
}
for (Re j = i; j <= n; ++j) g[j] = f[j], hea[j] = f[j] = 0;
cnt = 0, f[i] = m + 1;
for (Re j = m; j; --j)
{
int u = a[j].r, v = a[j].l;
if (f[v] || u < i || v < i) continue;
add(u, v);
if (f[u]) dfs(v, j);
}
for (Re j = i; j <= n; ++j)
if (f[j] && g[j]) ++ans[min(f[j], g[j])];
}
for (Re i = m; i; --i) ans[i] += ans[i + 1];
for (Re i = 1; i <= m + 1; ++i) write(ans[i]);
return 0;
}
[省选联考 2021 B 卷] 数对
洛谷P7515、LOJ#3505
给定\(n\)个正整数\(a_i\),请你求出有多少个数对\((i,j)\)满足\(1 \le i \le n\),\(1 \le j \le n\),\(i \ne j\)且\(a_i\)是\(a_j\)的倍数
\(2 \leq n \leq 2 \times 10^5\),\(1 \leq a_i \leq 5 \times 10^5\)
由于\(a_i \leq 5 \cdot 10^5\)
可以记录\(cnt_i\)表示值为\(i\)的个数,然后枚举\(i\)的所有的倍数计算答案
时间复杂度为\(\mathcal O(nlog\ n)\)
#include<bits/stdc++.h>
using namespace std;
#define Re register int
typedef long long ll;
int n, mx, cnt[500005];
ll ans;
inline int read()
{
char c = getchar();
int ans = 0;
while (c < 48 || c > 57) c = getchar();
while (c >= 48 && c <= 57) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
return ans;
}
int main()
{
n = read(), ans = -n;
for (Re i = 1; i <= n; ++i)
{
int u = read();
mx = max(mx, u), ++cnt[u];
}
for (Re i = 1; i <= mx; ++i)
if (cnt[i])
for (Re j = i; j <= mx; j += i) ans += 1ll * cnt[i] * cnt[j];
printf("%lld", ans);
return 0;
}
Day2
[省选联考 2021 A/B 卷] 宝石
洛谷P7518、LOJ#3502
给了一棵\(n\)个点的树,每个点上的宝石种类为\(w_i\),收集宝石只能按\(P_1,P_2...P_c\)的顺序收集
\(q\)个询问,每次给出起点\(s_i\)和终点\(t_i\),求从\(s_i\)到\(t_i\)的最短路线中最多能收集多少宝石
\(1 \leq n,q \leq 2 \times 10^5\),\(1 \leq c \leq m \leq 5 \times 10^4\),\(1 \leq w_i \leq m\)
对于一个询问\(u\)->\(v\),我们可以找到它们的\(lca(u,v)=w\),然后将询问拆成拆成向上和向下(\(u\)->\(w\),\(w\)->\(v\))两部分
考虑向上的部分怎么计算,向上的先是跳到往上的离它最近的\(P_1\)种宝石,然后再往上跳到\(P_2\)种宝石、\(P_3\)种宝石......
我们可以设一个\(dp\):\(f_{x,i}\)表示从\(x\)往上匹配(假设\(x\)与第\(P_j\)种宝石匹配),从\(P_j\)开始一直匹配到\(P_{j+2^i}\)种宝石,第\(P_{j+2^i}\)种宝石的最大深度会是多少
用倍增求出这个\(dp\)后,对于每一个点,我们可以找出它向上离它最近的第\(P_1\)种宝石,向上的答案就是找到这个第\(P_1\)种宝石后,往上匹配使得深度不小于\(dep_w\),最多能匹配到多少个宝石,同样用倍增来处理,计算向上的答案所需要的复杂度是\(\Theta((n+q)log\ n)\)
发现这题有很多种做法,整理了其中几种(以下计算时间复杂度把\(m\)、\(c\)、\(q\)均看作与\(n\)一个级别的)
法一:
二分+倍增
对于一个询问,已知向上一段的答案,记为\(x\),我们可以二分一个答案,上界为\(c\),下界为\(x+1\),下界不能为\(x\)是以为这条向下的链上不一定存在第\(x\)种宝石,当二分到的答案都不合法时再将答案记为\(x\),对于二分到的答案,记为\(mid\),我们要找\(v\)往上的离它最近的\(P_{mid}\)种宝石在哪
计算向下的答案,可以把询问离线,放在\(v\)上,遍历到某个节点时,用栈存这个节点向上最近的\(P_i\)种宝石在哪,然后判断\(P_{mid}\)是否存在以及深度是否不小于\(dep_w\),跳到\(P_{mid}\)后,再往上倍增去跳(和向上求解答案时类似),然后记能跳到的深度至少为\(dep_w\)的宝石为\(y\),比较\(y\)和\(x\)的大小关系,如果\(y \leq x+1\),那么答案\(mid\)便是合法的
时间复杂度为\(\mathcal O(nlog^2n)\)
法二:
二分+倍增+主席树
向上的处理完后,处理向下的,二分一个答案,要找向上第一个\(P_{mid}\)宝石在哪里
对于节点\(x\),找它向上的第一个\(P_i\)种宝石,当\(x\)上的宝石为第\(P_i\)种时,要找的就是这个节点,不然从\(x\)往上找和从\(fa_x\)往上找是一样的,可以用主席树预处理每个点往上找最近的第\(P_i\)个宝石在哪里
找到第一个\(P_{mid}\)种宝石后,便可以如上做法倍增往上跳,这样就可以在线做出答案
时间复杂度为\(\mathcal O(nlog^2n)\)
法三:
整体二分+倍增+吉司机线段树
对于向上的询问,同上二分答案,但是由于找离它最近的\(P_{mid}\)种宝石不好找,如果找到的话也可以同上跳倍增
可以把所有的询问离线起来,整体二分,要找离它最近的\(P_{mid}\)种宝石,对于二分到第\(P_{mid}\)种宝石的点,按树上\(dfs\)序排序,将所有的\(P_{mid}\)种宝石找出来,对它的子树\(dfs\)序所在的区间,用\(dep\)去进行取\(max\)操作,这个用吉司机线段树维护即可
时间复杂度为\(\mathcal O(nlog^2n)\)
法四:
点分治+二分
路径问题考虑用点分治来解决,对于点分治重心\(x\),将询问拆成\(u\)->\(x\)和\(x\)->\(v\),\(u\)、\(v\)在\(x\)的不同儿子的子树内
点分治后,对于当前\(x\)的所有儿子节点,预处理从它们的宝石开始往上\(+1\)/\(-1\)地跳宝石,最多能跳到多少宝石
对于\(u\)->\(x\),找\(u\)->\(x\)上的第一个\(P_1\)种宝石的位置,然后通过上面的预处理便能知道从\(P_1\)开始往上\(+1\)地跳宝石直到\(x\)最多能跳到多少宝石
对于\(x\)->\(v\),往下遍历到\(v\),用栈存经过的宝石,二分答案,找往上第一个\(P_{mid}\)宝石,通过上面的预处理便能知道从\(P_{mid}\)开始往上\(-1\)地跳宝石直到\(x\)最多能跳到多少宝石,判断一下可不可行
时间复杂度为\(\mathcal O(nlog\ n)\)
法五:
可撤销并查集
离线,把询问向上的答案和询问的编号存在\(lca(u,v)=w\)上
向下遍历节点时,当前的宝石为\(P_x\),那么便可把答案为\(P_{x-1}\)的变为答案为\(P_x\)的,用并查集按秩合并,回溯时要拆开,可以用可撤销并查集维护,加入一个询问的话加到对应的并查集上,回溯时再删掉即可
时间复杂度为\(\mathcal O(nlog\ n)\)
以下为法一的代码:
#include<bits/stdc++.h>
using namespace std;
#define Re register int
const int N = 200005, M = 50005;
struct quer
{
int s, d, id;
};
int n, m, c, cnt, lg[N], p[M], a[M], val[N], hea[N], nxt[N << 1], to[N << 1], dep[N], g[N], fa[N][19], f[N][19], ff[N][19], ans[N];
deque<int> tt[M];
vector<quer> qu[N];
inline int read()
{
char c = getchar();
int ans = 0;
while (c < 48 || c > 57) c = getchar();
while (c >= 48 && c <= 57) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
return ans;
}
inline void write(int x)
{
int num = 0;
char sc[15];
if (!x) sc[num = 1] = 48;
while (x) sc[++num] = x % 10 + 48, x /= 10;
while (num) putchar(sc[num--]);
putchar('\n');
}
inline bool cmp(int x, int y)
{
return p[x] < p[y];
}
inline int findd(int x)
{
if (x < p[a[1]]) return 0;
int l = 2, r = c, s = 1;
while (l <= r)
{
int mid = l + r >> 1;
if (x >= p[a[mid]]) s = mid, l = mid + 1;
else r = mid - 1;
}
return x ^ p[a[s]] ? 0 : a[s];
}
inline void add(int x, int y)
{
nxt[++cnt] = hea[x], to[cnt] = y, hea[x] = cnt;
}
inline void dfs(int x)
{
if (val[x]) tt[val[x]].push_back(x);
dep[x] = dep[fa[x][0]] + 1, g[x] = tt[1].back();
if (val[x])
{
if (val[x] < c)
{
f[x][0] = tt[val[x] + 1].back();
for (Re i = 1; f[x][i - 1]; ++i) f[x][i] = f[f[x][i - 1]][i - 1];
}
if (val[x] > 1)
{
ff[x][0] = tt[val[x] - 1].back();
for (Re i = 1; ff[x][i - 1]; ++i) ff[x][i] = ff[ff[x][i - 1]][i - 1];
}
}
for (Re i = 1; fa[x][i - 1]; ++i) fa[x][i] = fa[fa[x][i - 1]][i - 1];
for (Re i = hea[x]; i; i = nxt[i])
{
int u = to[i];
if (u == fa[x][0]) continue;
fa[u][0] = x;
dfs(u);
}
if (val[x]) tt[val[x]].pop_back();
}
inline int get_lca(int x, int y)
{
if (x == y) return x;
if (dep[x] < dep[y]) x ^= y ^= x ^= y;
for (Re i = lg[dep[x] - dep[y]]; dep[x] > dep[y]; i = lg[dep[x] - dep[y]]) x = fa[x][i];
if (x == y) return x;
for (Re i = lg[dep[x] - 2]; i >= 0; --i)
if (fa[x][i] ^ fa[y][i]) x = fa[x][i], y = fa[y][i];
return fa[x][0];
}
inline int get_up(int x, int y)
{
x = g[x];
if (dep[x] < y) return 0;
for (Re i = lg[dep[x] - y]; i >= 0; --i)
if (dep[f[x][i]] >= y) x = f[x][i];
return val[x];
}
inline int get_up1(int x, int y)
{
for (Re i = lg[dep[x] - y]; i >= 0; --i)
if (dep[ff[x][i]] >= y) x = ff[x][i];
return val[x];
}
inline void dfs1(int x)
{
if (val[x]) tt[val[x]].push_back(x);
int u = qu[x].size();
for (Re i = 0; i < u; ++i)
{
int l = qu[x][i].s + 1, r = c, s = qu[x][i].s, ss = qu[x][i].s + 1, h = qu[x][i].d;
while (l <= r)
{
int mid = l + r >> 1;
if (dep[tt[mid].back()] >= h && get_up1(tt[mid].back(), h) <= ss) s = mid, l = mid + 1;
else r = mid - 1;
}
ans[qu[x][i].id] = s;
}
for (Re i = hea[x]; i; i = nxt[i])
{
int u = to[i];
if (u == fa[x][0]) continue;
dfs1(u);
}
if (val[x]) tt[val[x]].pop_back();
}
int main()
{
n = read(), m = read(), c = read();
for (Re i = 1; (1 << i) <= n; ++i) lg[1 << i] = i;
for (Re i = 3; i <= n; ++i)
if (!lg[i]) lg[i] = lg[i - 1];
for (Re i = 1; i <= c; ++i) p[i] = read(), a[i] = i, tt[i].push_back(0);
sort(a + 1, a + c + 1, cmp);
for (Re i = 1; i <= n; ++i) val[i] = findd(read());
for (Re i = 1; i < n; ++i)
{
int u = read(), v = read();
add(u, v), add(v, u);
}
dfs(1);
m = read();
for (Re i = 1; i <= m; ++i)
{
int u = read(), v = read(), w = dep[get_lca(u, v)];
qu[v].push_back(quer{get_up(u, w), w, i});
}
dfs1(1);
for (Re i = 1; i <= m; ++i) write(ans[i]);
return 0;
}
以下为法五的代码:
#include<bits/stdc++.h>
using namespace std;
#define Re register int
const int N = 200005, M = 50005;
struct quer
{
int s, id;
};
int n, m, c, cnt, lg[N], p[M], a[M], val[N], hea[N], nxt[N << 1], to[N << 1], dep[N], g[N], fa[N][19], f[N][19], rt[M], faa[N], h[N], hh[N], ans[N];
deque<int> tt[M];
vector<quer> qu[N];
vector<int> quu[N];
inline int read()
{
char c = getchar();
int ans = 0;
while (c < 48 || c > 57) c = getchar();
while (c >= 48 && c <= 57) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
return ans;
}
inline void write(int x)
{
int num = 0;
char sc[15];
if (!x) sc[num = 1] = 48;
while (x) sc[++num] = x % 10 + 48, x /= 10;
while (num) putchar(sc[num--]);
putchar('\n');
}
inline bool cmp(int x, int y)
{
return p[x] < p[y];
}
inline int findd(int x)
{
if (x < p[a[1]]) return 0;
int l = 2, r = c, s = 1;
while (l <= r)
{
int mid = l + r >> 1;
if (x >= p[a[mid]]) s = mid, l = mid + 1;
else r = mid - 1;
}
return x ^ p[a[s]] ? 0 : a[s];
}
inline void add(int x, int y)
{
nxt[++cnt] = hea[x], to[cnt] = y, hea[x] = cnt;
}
inline void dfs(int x)
{
if (val[x]) tt[val[x]].push_back(x);
dep[x] = dep[fa[x][0]] + 1, g[x] = tt[1].back();
if (val[x] && val[x] < c)
{
f[x][0] = tt[val[x] + 1].back();
for (Re i = 1; f[x][i - 1]; ++i) f[x][i] = f[f[x][i - 1]][i - 1];
}
for (Re i = 1; fa[x][i - 1]; ++i) fa[x][i] = fa[fa[x][i - 1]][i - 1];
for (Re i = hea[x]; i; i = nxt[i])
{
int u = to[i];
if (u == fa[x][0]) continue;
fa[u][0] = x;
dfs(u);
}
if (val[x]) tt[val[x]].pop_back();
}
inline int get_lca(int x, int y)
{
if (x == y) return x;
if (dep[x] < dep[y]) x ^= y ^= x ^= y;
for (Re i = lg[dep[x] - dep[y]]; dep[x] > dep[y]; i = lg[dep[x] - dep[y]]) x = fa[x][i];
if (x == y) return x;
for (Re i = lg[dep[x] - 2]; i >= 0; --i)
if (fa[x][i] ^ fa[y][i]) x = fa[x][i], y = fa[y][i];
return fa[x][0];
}
inline int get_up(int x, int y)
{
x = g[x];
if (dep[x] < y) return 0;
for (Re i = lg[dep[x] - y]; i >= 0; --i)
if (dep[f[x][i]] >= y) x = f[x][i];
return val[x];
}
inline int find_faa(int x)
{
return x > m ? x - m - 1 : find_faa(faa[x]);
}
inline int mer(int x, int y)
{
if (!x || !y) return x | y;
if (h[x] > h[y]) x ^= y ^= x ^= y;
hh[x] = h[y], faa[x] = y;
if (h[x] == h[y]) ++h[y];
return y;
}
inline void calc(int x)
{
int u = qu[x].size(), v = quu[x].size(), w;
bool p = 0;
if (val[x] && (rt[val[x]] || rt[val[x] - 1]))
{
int uu = rt[val[x]], vv = rt[val[x] - 1];
faa[rt[val[x]] = mer(uu, vv)] = val[x] + m + 1, rt[val[x] - 1] = 0;
if (rt[val[x]] == uu) w = vv;
else w = uu, p = 1;
}
for (Re i = 0; i < u; ++i) faa[rt[qu[x][i].s] = mer(qu[x][i].id, rt[qu[x][i].s])] = qu[x][i].s + m + 1;
for (Re i = 0; i < v; ++i) ans[quu[x][i]] = find_faa(quu[x][i]);
for (Re i = hea[x]; i; i = nxt[i])
if (to[i] ^ fa[x][0]) calc(to[i]);
for (Re i = u - 1; i >= 0; --i)
if (rt[qu[x][i].s] ^ qu[x][i].id) h[rt[qu[x][i].s]] = hh[qu[x][i].id];
else rt[qu[x][i].s] = 0;
if (val[x] && rt[val[x]])
if (p)
if (w) faa[rt[val[x] - 1] = rt[val[x]]] = val[x] + m, faa[rt[val[x]] = w] = val[x] + m + 1, h[rt[val[x] - 1]] = hh[w];
else faa[rt[val[x] - 1] = rt[val[x]]] = val[x] + m, rt[val[x]] = 0;
else if (w) faa[rt[val[x] - 1] = w] = val[x] + m, h[rt[val[x]]] = hh[w];
}
int main()
{
n = read(), m = read(), c = read();
for (Re i = 1; (1 << i) <= n; ++i) lg[1 << i] = i;
for (Re i = 3; i <= n; ++i)
if (!lg[i]) lg[i] = lg[i - 1];
for (Re i = 1; i <= c; ++i) p[i] = read(), a[i] = i, tt[i].push_back(0);
sort(a + 1, a + c + 1, cmp);
for (Re i = 1; i <= n; ++i) val[i] = findd(read());
for (Re i = 1; i < n; ++i)
{
int u = read(), v = read();
add(u, v), add(v, u);
}
dfs(1);
m = read();
for (Re i = 1; i <= m; ++i)
{
int u = read(), v = read(), w = get_lca(u, v), s = get_up(u, dep[w]);
h[faa[i] = i] = 1, qu[w].push_back(quer{s, i}), quu[v].push_back(i);
}
calc(1);
for (Re i = 1; i <= m; ++i) write(ans[i]);
return 0;
}
[省选联考 2021 A/B 卷] 滚榜
洛谷P7519、LOJ#3503
有\(n\)只队伍,记第\(i\)只队伍最后一个小时前的过题数为\(a_i\),最后一个小时内的过题数为\(b_i\)
排行榜上队伍按照过题数从大到小进行排名,若两支队伍过题数相同,则编号小的队伍排名靠前
初始按\(a_i\)进行排名,主办方以\(b_i\)不降的顺序公布每只队伍最后一个小时的过题数\(b_i\),并把\(b_i\)统计进那只队伍的过题数中,每次公布结果后的队伍都成为了排行榜上新的的第一名,求最终排行榜的队伍排名顺序有几种情况
\(m = \sum_{i=1}^n b_i\)
\(1 \leq n \leq 13\),\(1 \leq m \leq 500\),\(0 \leq a_i \leq 10^4\)
要求每次被公布结果的队伍都成为新排行榜上的第一名,以\(b_i\)不降的顺序公布每只队伍,即最终排名从最后一名到第一名,它们的\(b_i\)是不降的,还有,过题量一样的,编号小的在前
看到数据范围\(n \leq 13\),不难想到状压\(dp\)
可以发现任意一种排名能被表示出来当且仅当从最后一名到第一名,他们的\(b_i\)不降,且最后一名在被公布\(b_i\)的瞬间,此时是第一次公布结果,他会比\(a_i\)最大的排名靠前,在满足前面要求的前提下还要满足所有的\(b_i\)加起来不超过\(m\)
由于总排名最后一名一定会在第一次公布,并且它是大于原来的第一名的,且其他所有队伍的总排名最后均会在其之前,所以可以先把所有的队伍的\(a+b\)都补到一样多,使得\(m\)减少
设\(f_{S,i,j}\)表示在当前状态\(S\)(一个二进制数,从低到高位,为\(1\)表示当前位已经被公布了\(b\)的值,为\(0\)表示目前没有被公布),目前最后一个被公布\(b\)的值(即目前排名最高的)是\(i\),且目前花费的总代价为\(j\)使得还没被公布的队伍的\(a+b\)与第\(i\)只队伍的\(a+b\)一样多
当\(S\)二进制只有一位为\(1\),即当前只有第\(i\)只队伍被公布\(b\)的值时,它的排名暂时是第一名,所以要让它暂时比\(a\)值第一名(记为\(x\))排名靠前,又因为初始时把每只队伍都赋了一定\(b\)值,使得他们的总值\(a+b\)与\(a_x\)一样多,所以只要记录一下\(x\),如果\(i<x\),那么就只需要初始补全的数量,否则需要额外多\(1\),使得\(a_i+b_i\)比\(a_x\)值多\(1\),此时还要把除\(i\)以外的其他\(n-1\)只队伍的\(b\)值多\(1\),将他们的\(a+b\)值补到和第\(i\)只队伍一样多
当\(S\)二进制不只有一位\(1\)时,当前最后一只被公布\(b\)的值的队伍为\(i\),枚举当前倒数第二只被公布\(b\)的值的队伍为\(k\),由于之前每次都把没有被公布\(b\)的值的队伍的\(a+b\)值补到和当前最高排名的\(a+b\)值一样多,所以当前的第\(i\)只队伍的\(a+b\)值与第\(k\)只队伍一样多,由于它们初始的\(a_i\)、\(a_k\)已知,又\(b_i \geq b_k\),所以\((a_i+b_i)-(a_k+b_k) \geq max(a_i-a_k,0)\),又如果\(i > k\)时,\((a_i+b_i)-(a_k+b_k) \geq 1\),所以\((a_i+b_i)-(a_k+b_k) \geq max(a_i-a_k,i>k)\),把\(b_i\)增加后要记得把其他没有被公布的队伍的\(b\)值增加,使得\(a+b\)值与\(a_i+b_i\)一样多,记\(S\)中\(1\)的个数为\(t\),则总方程:
时间复杂度\(\mathcal O(2^nn^2m)\)
#include<bits/stdc++.h>
using namespace std;
#define Re register int
typedef long long ll;
const int N = 8200, M = 505;
int n, m, nn, sum, mx, t, a[14], d[14], f[N][14][M];
ll ans;
inline int read()
{
char c = getchar();
int ans = 0;
while (c < 48 || c > 57) c = getchar();
while (c >= 48 && c <= 57) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
return ans;
}
inline int max(int x, int y)
{
return x > y ? x : y;
}
int main()
{
n = read(), m = read(), nn = 1 << n;
for (Re i = 0; i < n; ++i)
{
a[i]= read(), sum += a[i];
if (a[i] > mx) mx = a[i], t = i;
}
m -= mx * n - sum;
if (m < 0)
{
putchar(48);
return 0;
}
for (Re i = 1; i < nn; ++i)
{
int s = 0;
for (Re j = 0; j < n; ++j)
if ((i >> j) & 1) d[++s] = j;
if (s == 1)
{
int u = d[1];
if (u <= t) f[i][u][0] = 1;
if (u > t && n <= m) f[i][u][n] = 1;
continue;
}
for (Re j = 1; j <= s; ++j)
{
int jj = d[j], u = i ^ (1 << jj);
for (Re t = 1; t <= s; ++t)
{
if (t == j) continue;
int l = d[t], v = a[jj] - a[l];
v = max(v, jj > l);
for (Re k = (n - s + 1) * v; k <= m; ++k) f[i][jj][k] += f[u][l][k - (n - s + 1) * v];
}
}
}
for (Re i = 0; i < n; ++i)
for (Re j = 0; j <= m; ++j) ans += f[nn - 1][i][j];
printf("%lld", ans);
return 0;
}
[省选联考 2021 A 卷] 支配
洛谷P7520、LOJ#3504
给定一张\(n\)个点\(m\)条边的有向图\(G\),其顶点从\(1\)到\(n\)编号
对于任意两个点\(u,v\),若从顶点\(1\)出发到达顶点\(v\)的所有路径都需要经过顶点\(u\),则称顶点\(u\)支配顶点\(v\)。特别地,每个顶点支配其自身
对于任意一个点\(v\),我们将图中支配顶点\(v\)的顶点集合称为\(v\)的受支配集\(D_v\)
有\(q\)次互相独立的询问,每次询问给出一条有向边,要判断在图\(G\)中加入该条边后,有多少个顶点的受支配集发生了变化
\(1 \leq n \leq 3 \times 10^3\),\(1 \leq m \leq 2 \times n\),\(1 \leq q \leq 2 \times 10^4\)
首先暴力求出每个点的受支配集
每次可以任意删除一个点,判断从\(1\)出发能到达哪些点,如果删除\(x\)后,\(1\)到不了\(y\),由于题目保证\(1\)号点能到达任意一个点,所以说明从\(1\)到\(y\)一定要经过\(x\)
发现到,每个点的受支配集一定是呈现树的形态,假设点\(x\)的受支配集为\(a_1,a_2,...a_t\),又从\(1\)到\(x\)的所有路径都要经过它的所有受支配集,不妨假设一条路径为\(a_1\)->\(a_2\)->\(a_3\)->...->\(a_t\)(其中\(a_1=1\),\(a_t=x\)),其中每个\(a_i\)只经过一次,因为如果有一个点重复经过了两次,这两次之间的那些点就没有必要经过
由于\(a_i\)支配\(x\),所以\(1\)->\(x\)必须经过\(a_i\),假设\(a_j(1 \leq j < i)\)不支配\(a_i\),即\(1\)->\(a_i\)的路径可以不经过\(a_j\),由于\(a_i\)->\(a_t\)的路径可以不经过\(a_j\),那么\(1\)->\(a_t\)的路径也可以不经过\(a_j\),那么\(a_j\)就不支配\(x\),与前面矛盾,所以\(a_j(1 \leq j < i)\)支配\(a_i\),所以每个点的受支配集一定是呈现树的形态,其中一个点它的所有祖先就是它受支配集的集合,我们可以先建出这棵支配树,每个点支配它的所有孩子节点
记点\(x\)在支配树上的父亲为\(fa_x\)
又因为每个点的受支配集就是指向它的所有点的受支配集的交集再加上这个点
加入一条边\(s\)->\(t\),判断是否有改变\(t\)的受支配集,如果没有改变\(t\)的受支配集,那自然不可能通过\(t\)去改变其他顶点的受支配集
假设改变了点\(x\)的受支配集,只可能是使\(x\)的受支配集减少,如果\(x\)的受支配集改变后仍旧还存在\(fa_x\),那么\(fa_x\)的受支配集肯定发生了改变,又一个点的受支配集改变会使得它所有孩子的受支配集都改变,所以我们只要考虑\(x\)的受支配集中不存在\(fa_x\)的即可,后面在去覆盖它的孩子即可
边\(s\)->\(t\)要使\(1\)->\(x\)不需要经过\(fa_x\)(其中\(fa_x \neq s\)且\(fa_x \neq t\)),那么肯定存在一条路径\(1\)->\(s\)->\(t\)->\(x\),其中不经过\(fa_x\),\(s\)->\(t\)只有一条边,肯定不经过\(fa_x\),所以只需考虑\(1\)->\(s\)和\(t\)->\(x\),\(1\)->\(s\)不经过\(fa_x\),只需要满足\(s\)的受支配集中不存在\(fa_x\),即\(fa_x\)不为\(s\)的祖先,\(t\)->\(x\)不经过\(fa_x\),我们可以预先处理一下,建原图的反图,对于\(x\),删除点\(fa_x\),看\(x\)能跑到哪些点,那些点就是对于\(x\)来说可行的\(t\)的集合
对于一组询问\(s\)->\(t\),枚举\(x\),判断\(fa_x\)是否为\(s\)的祖先,可以预先处理\(dfs\)序来判断,再判断\(x\)是否可以对\(t\)做贡献,如果均可以的话,把\(x\)标记一下,后面再去遍历整棵支配树,对于一个受支配集发生改变的节点\(x\),它的所有孩子的受支配集均会发生改变
时间复杂度为\(\mathcal O(n(n+q))\)
#include<bits/stdc++.h>
using namespace std;
#define Re register int
typedef long long ll;
const int N = 3005;
int n, m, qu, cnt, l, r, tim, ans, lg[N], q[N], fa[N], dfn[N], dep[N], siz[N], f[N][12], hea[N], nxt[N << 1], to[N << 1], hea1[N], nxt1[N * N], to1[N * N], rd[N], hea2[N], nxt2[N], to2[N], hea3[N], nxt3[N << 1], to3[N << 1];
bool b[N], p[N][N];
inline int read()
{
char c = getchar();
int ans = 0;
while (c < 48 || c > 57) c = getchar();
while (c >= 48 && c <= 57) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
return ans;
}
inline void write(int x)
{
int num = 0;
char sc[15];
while (x) sc[++num] = x % 10 + 48, x /= 10;
while (num) putchar(sc[num--]);
putchar('\n');
}
inline void add(int x, int y)
{
nxt[++cnt] = hea[x], to[cnt] = y, hea[x] = cnt;
nxt3[cnt] = hea3[y], to3[cnt] = x, hea3[y] = cnt;
}
inline void add1(int x, int y)
{
nxt1[++cnt] = hea1[x], to1[cnt] = y, hea1[x] = cnt, ++rd[y];
}
inline void add2(int x, int y)
{
nxt2[++cnt] = hea2[x], to2[cnt] = y, hea2[x] = cnt;
}
inline void calc(int x)
{
for (Re i = 2; i <= n; ++i) b[i] = 0;
b[q[l = r = 0] = 1] = b[x] = 1;
while (l <= r)
{
int x = q[l++];
for (Re i = hea[x]; i; i = nxt[i])
{
int u = to[i];
if (!b[u]) b[q[++r] = u] = 1;
}
}
for (Re i = 2; i <= n; ++i)
if (!b[i]) add1(x, i);
}
inline void calc1(int x)
{
int y = fa[x];
for (Re i = 1; i <= n; ++i) b[i] = 0;
b[q[l = r = 0] = x] = b[y] = 1;
while (l <= r)
{
int x = q[l++];
for (Re i = hea3[x]; i; i = nxt3[i])
{
int u = to3[i];
if (!b[u]) b[q[++r] = u] = 1;
}
}
b[y] = 0;
for (Re i = 1; i <= n; ++i)
if (b[i]) p[i][x] = 1;
}
inline void dfs(int x)
{
dfn[x] = ++tim, dep[x] = dep[f[x][0] = fa[x]] + 1, siz[x] = 1;
for (Re i = 1; f[x][i - 1]; ++i) f[x][i] = f[f[x][i - 1]][i - 1];
for (Re i = hea2[x]; i; i = nxt2[i])
{
int u = to2[i];
dfs(u);
siz[x] += siz[u];
}
}
inline int lca(int x, int y)
{
if (x == y) return x;
if (dep[x] < dep[y]) x ^= y ^= x ^= y;
for (Re i = lg[dep[x] - dep[y]]; i >= 0; --i)
if (dep[f[x][i]] >= dep[y]) x = f[x][i];
if (x == y) return x;
for (Re i = lg[dep[x] - 2]; i >= 0; --i)
if (f[x][i] ^ f[y][i]) x = f[x][i], y = f[y][i];
return f[x][0];
}
inline void dfs1(int x)
{
if (b[x])
{
ans += siz[x];
return;
}
for (Re i = hea2[x]; i; i = nxt2[i])
{
int u = to2[i];
dfs1(u);
}
}
int main()
{
n = read(), m = read(), qu = read();
for (Re i = 1; (1 << i) <= n; ++i) lg[1 << i] = i;
for (Re i = 3; i <= n; ++i)
if (!lg[i]) lg[i] = lg[i - 1];
for (Re i = 0; i < m; ++i)
{
int u = read(), v = read();
add(u, v);
}
cnt = 0;
for (Re i = 2; i <= n; ++i) add1(1, i);
for (Re i = 2; i <= n; ++i) calc(i);
q[l = r = 0] = 1, cnt = 0;
while (l <= r)
{
int x = q[l++];
for (Re i = hea1[x]; i; i = nxt1[i])
{
int u = to1[i];
if (!(--rd[u])) fa[q[++r] = u] = x, add2(x, u);
}
}
for (Re i = 2; i <= n; ++i) calc1(i);
dfs(1);
while (qu--)
{
int u = read(), v = read();
if (dep[lca(u, v)] >= dep[v] - 1)
{
puts("0");
continue;
}
ans = 0;
for (Re i = 1; i <= n; ++i)
if (p[v][i] && (dfn[u] < dfn[fa[i]] || dfn[u] >= dfn[fa[i]] + siz[fa[i]])) b[i] = 1;
else b[i] = 0;
dfs1(1);
write(ans);
}
return 0;
}
[省选联考 2021 B 卷] 取模
洛谷P7521、LOJ#3508
给定\(n\)个正整数\(a_i\),请你在其中选出三个数\(i,j,k(i \neq j, i \neq k, j \neq k)\),使得\((a_i+a_j)\ mod\ a_k\)的值最大
\(3 \leq n \leq 2 \times 10^5\),\(1 \leq a_i \leq 10^8\)
先排个序,让\(a\)从小到大排序,枚举模数\(a_k\),让其他所有的数对其取模,记\(b_i=a_i\ mod\ a_k\),要让\((a_i+a_j)\ mod\ a_k\)最大,即让\((b_i+b_j)\ mod\ a_k\)最大
又\(b_i,b_j<a_k\),所以我们可以分\(b_i+b_j<a_k\)和\(b_i+b_j \geq a_k\)两种情况讨论
当\(b_i+b_j<a_k\)时,\((b_i+b_j)\ mod\ a_k=b_i+b_j\)我们可以把\(b\)从小到大排序,然后用双指针找\(b_i+b_j\)小于\(a_k\)的最大值
当\(b_i+b_j \geq a_k\)时,\((b_i+b_j)\ mod\ a_k=b_i+b_j-a_k\),\(b_i+b_j\)的最大值就是排序后的最后两个值的和
这样便可以做到\(\Theta(n^2log\ n)\)了
枚举模数\(a_k\)时,我们可以从大到小枚举,记录目前最优答案为\(ans\),如果\(a_k \leq ans\),那么便可以退出,对于相同的\(a_k\),只要枚举其中一个即可
当枚举到\(a_t\)且\(a_t\)需要进去枚举时,则\(ans< a_t < a_{t+1} \leq a_{t+2}...\leq a_{n}\)
对于\(a_i\),以\(a_i\)为模数的答案至少为\(a_{i-1}+a_{i-2}-a_i\),则对于\(t+1 \leq i \leq n\),均满足\(a_{i-1}+a_{i-2}-a_i \leq ans < a_t\),即满足\(a_i-a_t>(a_{i-1}-a_t)+(a_{i-2}-a_t)\)
令\(c_i=a_i-a_t(t < i \leq n)\),则\(c_i=c_{i-1}+c_{i-2}(t+3 \leq i \leq n)\),则\(c_i\)至少是按斐波那契数列增长的,所以至多枚举\(log\ V\)个模数
时间复杂度为\(\mathcal O(n\ log\ n\ log\ V)\)
#include<bits/stdc++.h>
using namespace std;
#define Re register int
const int N = 200005;
int n, ans, a[N], b[N];
inline int read()
{
char c = getchar();
int ans = 0;
while (c < 48 || c > 57) c = getchar();
while (c >= 48 && c <= 57) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
return ans;
}
inline int max(int x, int y)
{
return x > y ? x : y;
}
int main()
{
n = read();
for (Re i = 1; i <= n; ++i) a[i] = read();
sort(a + 1, a + n + 1);
for (Re i = n; a[i] > ans; --i)
if (a[i] ^ a[i + 1])
{
for (Re j = 1; j < i; ++j) b[j] = a[j] % a[i];
for (Re j = i; j < n; ++j) b[j] = a[j + 1] % a[i];
sort(b + 1, b + n);
ans = max(ans, b[n - 2] + b[n - 1] - a[i]);
for (Re j = n - 1, k = 1; j > k; --j)
{
if (b[j] + b[k] >= a[i]) continue;
while (j > k + 1 && b[j] + b[k + 1] < a[i]) ++k;
ans = max(ans, b[j] + b[k]);
}
}
printf("%d", ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号