[SDOI2017]天才黑客(前后缀优化建图+Dijkstra)
题目:洛谷P3783、LOJ#2270
题目描述:
给定\(n\)个点,\(m\)条边的有向图,还有一棵\(k\)个节点的树,保证有向图能从\(1\)号节点通过某些有向边到达任何图上的其他节点,通过图上的边\(i\)需要\(c_{i}\)时间,每条边有一个值\(d_{i}\),表示这条边上面的字符串\(S_{i}\)为从给定的\(k\)个节点的树的根节点一直到节点\(d_{i}\)的所有边上的字母连接起来构成的字符串,初始你的字符串为空,假设你现在的字符串为\(S\),经过一条边后,你需要消耗\(lcp(S, S_{d_{i}})\)时间使\(S=S_{d_{i}}\),求从\(1\)号节点所有其他节点的最少时间分别是多少
一共\(T\)组数据
\(T \leq 10\),\(n,m \leq 50000\),\(k \leq 20000\)
蒟蒻题解:
通过题意可得,两条边之间字符串的\(lcp\)相当于它们\(d_{i}\)的\(lca\)的深度
容易想到化边为点,把每条边拆成入点和出点,但是这样边数最多会达到\(m^{2}\)级别的,会拿到\(0\)分的好成绩
有一个树上的性质,把树上的所有节点按\(dfs\)序排序,则\(lcp(S_{i},S_{j})=min(lcp(S_{i},S_{i+1}),lcp(S_{i},S_{i+1}),...,lcp(S_{j-1},S_{j}))\)
我看很多题解提到这个有点类似后缀数组,但是身为只打过后缀数组模板的蒟蒻,我是用\(RMQ\)求\(lca\)的方法去理解的
取出一个图上的点\(u\)以及它周围的所有边,如下图
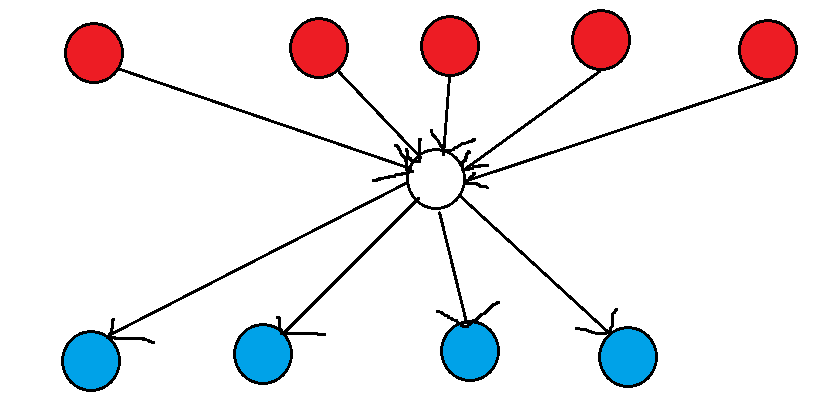
红点表示的是连向\(u\)的所有边的出点,蓝点表示从\(u\)连出去的所有边的入点
中间的点\(u\)没用,可以删去,就变成了\(m^{2}\)条边级别的暴力,如下图(太多边了,箭头就不打了,都是从上面指向下面)
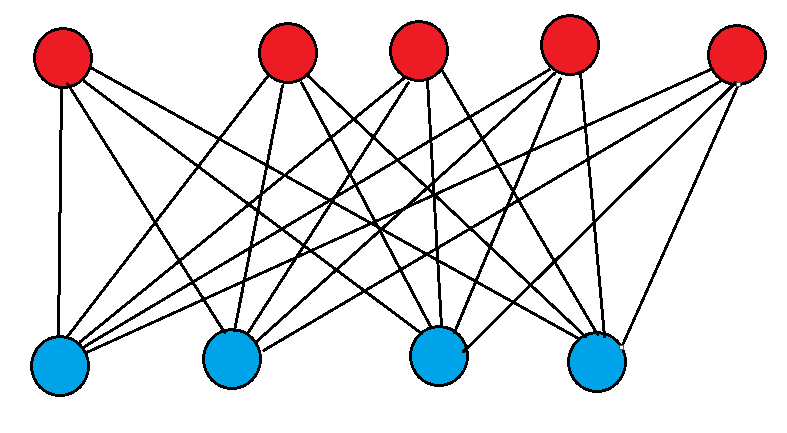
根据我们已知的性质,我们可以把所有的这些点按\(dfs\)序排序,对于两个点之间的\(lcp(a_{i},a_{j})\)可以用\(min(lcp(a_{i},a_{i+1}),lcp(a_{i+1},a_{i+2}),...,lcp(a_{j-1},a_{j}))\)代替,对于\(lcp(a_{k},a_{k+1})\)的贡献只和\(i \leq k < j\)且满足一个为红点,一个为蓝点的\((i,j)\)有关,由于这题是要求最小路径,建完图后要跑最短路,所以如果\(lcp(a_{k},a_{k+1})\)是最小的,那么红点要经过这条边,所以可以让每个点都像与它同色的上一个点或下一个点连边,以使红点能到达连接权值为\(lcp(a_{k},a_{k+1})\)的红点,并通过这条边到这个权值连接的蓝点,再通过这个蓝点到达它要到达的目标蓝点,所以红点和红点间、蓝点和蓝点间要么都是向右,要么都是向左以满足一个红点和蓝点组成的点对满足\(i \leq k < j\),而在前缀优化建图中,\(lcp(a_{k},a_{k+1})\)权值所在边的位置就要满足上面的红点是小于等于\(a_{k}\)的最靠右的点,下面的蓝点是大于等于\(a_{k+1}\)的最靠做的点,后缀优化建图同样的道理,前缀优化建图是建满足\(i \leq k < j\),其中\(i\)为红点,\(j\)为蓝点的路径,而后缀优化建图是建满足\(i \leq k < j\),其中\(i\)为蓝点,\(j\)为红点的路径,前缀优化建图如下(注意前缀优化建图和后缀优化建图不能用相同的点,得新建节点):
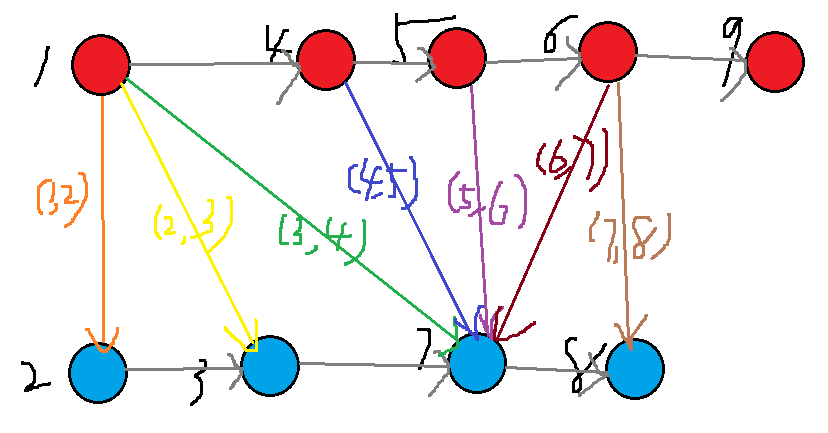
前缀优化建图方式:对于\(lcp(a_{i},a{i+1})\),在红点找\(dfs\)序小于等于\(a_{i}\)的最后一个点,在蓝点找\(dfs\)序大于等于\(a_{i+1}\)的第一个点,然后这两个点连权值为\(lcp(a_{i},a_{i+1})\)的边
时间复杂度为\(\Theta((N+M)log\ M)\),这里的\(N\)是\(n\)的很多倍(我的垃圾写法最多接近\(6\)倍),\(M\)是\(m\)的很多倍(我的垃圾写法最多接近\(36\)倍),但是由于远远跑不满,再加上\(n、m\)又不是特别大,所以可以轻松地通过此题
参考程序:
#include<bits/stdc++.h>
using namespace std;
#define Re register int
typedef long long ll;
const int N = 20005;
const int M = 50005;
const int K = 300005;
const ll Inf = 1e10;
struct edge
{
int x, y, t, w;
}eg[M];
struct inf
{
int s;
bool t;
}a[M];
struct info
{
int id;
ll dis;
friend bool operator < (info x, info y)
{
return x.dis > y.dis;
}
};
int T, n, m, k, num, cnt, cnt1, tim, siz, lg[M], hea1[N], nxt1[M], to1[M], fa[N], dfn[N], dep[N], g[M], f[M][19], pr[M][2], nt[M][2], id[K], hea[K], nxt[K * 6], to[K * 6], len[K * 6];
bool b[K];
ll dis[K], ans[M];
queue<int> q1[M], q2[M];
priority_queue<info> q;
inline int read()
{
char c = getchar();
int ans = 0;
while (c < 48 || c > 57) c = getchar();
while (c >= 48 && c <= 57) ans = (ans << 3) + (ans << 1) + (c ^ 48), c = getchar();
return ans;
}
inline void write(ll x)
{
int num = 0;
char sc[25];
if (!x) sc[num = 1] = 48;
while (x) sc[++num] = x % 10 + 48, x /= 10;
while (num) putchar(sc[num--]);
putchar('\n');
}
inline ll min(ll x, ll y)
{
return x < y ? x : y;
}
inline void add(int x, int y, int z)
{
nxt[++cnt] = hea[x], to[cnt] = y, len[cnt] = z, hea[x] = cnt;
}
inline void add1(int x, int y)
{
nxt1[++cnt1] = hea1[x], to1[cnt1] = y, hea1[x] = cnt1;
}
inline void dfs(int x)
{
dep[x] = dep[fa[x]] + 1, g[dfn[x] = ++tim] = x, f[tim][0] = dep[x];
for (Re i = hea1[x]; i; i = nxt1[i])
{
int u = to1[i];
if (u == fa[x]) continue;
fa[u] = x;
dfs(u);
g[++tim] = x, f[tim][0] = dep[x];
}
}
inline int lca(int x, int y)
{
if (x == y) return dep[x];
x = dfn[x], y = dfn[y];
if (x > y) x ^= y ^= x ^= y;
int z = lg[y - x + 1];
return min(f[x][z], f[y - (1 << z) + 1][z]);
}
inline bool cmp(inf x, inf y)
{
return dfn[eg[x.s].w] < dfn[eg[y.s].w];
}
inline void dij()
{
for (Re i = 0; i <= num; ++i) dis[i] = Inf, b[i] = 0;
q.push(info{0, dis[0] = 0});
while (!q.empty())
{
int x = q.top().id;
q.pop();
if (b[x]) continue;
b[x] = 1;
for (Re i = hea[x]; i; i = nxt[i])
{
int u = to[i];
if (dis[u] > dis[x] + len[i]) q.push(info{u, dis[u] = dis[x] + len[i]});
}
}
}
int main()
{
T = read();
for (Re i = 1; (1 << i) <= 4e4; ++i) lg[1 << i] = i;
for (Re i = 3; i <= 4e4; ++i)
if (!lg[i]) lg[i] = lg[i - 1];
while (T--)
{
n = read(), m = read(), k = read(), num = cnt = cnt1 = tim = hea[0] = 0;
for (Re i = 1; i <= n; ++i) ans[i] = Inf;
for (Re i = 1; i <= k; ++i) hea1[i] = fa[i] = dfn[i] = 0;
for (Re i = 1; i <= m; ++i)
{
int u = read(), v = read();
eg[i].t = read(), eg[i].w = read();
hea[num + 1] = hea[num + 2] = 0;
add(eg[i].x = num + 1, eg[i].y = num + 2, eg[i].t), id[++num] = u, id[++num] = v;
if (u == 1) add(0, eg[i].x, 0);
q1[u].push(i), q2[v].push(i);
}
for (Re i = 1; i < k; ++i)
{
int u = read(), v = read();
add1(u, v), add1(v, u);
u = read();
}
dep[0] = -1;
dfs(1);
for (Re i = 1; i <= 17; ++i)
for (Re j = 1; j <= tim - (1 << i) + 1; ++j)
f[j][i] = min(f[j][i - 1], f[j + (1 << (i - 1))][i - 1]);
for (Re i = 1; i <= n; ++i)
{
siz = 0;
while (!q1[i].empty()) a[++siz].s = q1[i].front(), a[siz].t = 1, q1[i].pop();
while (!q2[i].empty()) a[++siz].s = q2[i].front(), a[siz].t = 0, q2[i].pop();
sort(a + 1, a + siz + 1, cmp);
pr[0][0] = pr[0][1] = nt[siz + 1][0] = nt[siz + 1][1] = 0;
for (Re j = 1; j <= siz; ++j) pr[j][a[j].t] = j, pr[j][a[j].t ^ 1] = pr[j - 1][a[j].t ^ 1];
for (Re j = siz; j; --j) nt[j][a[j].t] = j, nt[j][a[j].t ^ 1] = nt[j + 1][a[j].t ^ 1];
for (Re j = num + 1; j <= num + (siz << 1); ++j) hea[j] = 0;
for (Re j = 1; j <= siz; ++j)
if (!a[j].t) id[num + j] = id[num + j + siz] = id[eg[a[j].s].y], add(eg[a[j].s].y, num + j, 0), add(eg[a[j].s].y, num + j + siz, 0);
else id[num + j] = id[num + j + siz] = id[eg[a[j].s].x], add(num + j, eg[a[j].s].x, 0), add(num + j + siz, eg[a[j].s].x, 0);
for (Re j = 1; j < siz; ++j)
{
if (pr[j][0] && pr[j][0] ^ pr[j + 1][0]) add(num + pr[j][0], num + pr[j + 1][0], 0);
if (pr[j][1] && pr[j][1] ^ pr[j + 1][1]) add(num + pr[j][1], num + pr[j + 1][1], 0);
if (pr[j][0] && nt[j + 1][1]) add(num + pr[j][0], num + nt[j + 1][1], lca(eg[a[j].s].w, eg[a[j + 1].s].w));
}
num += siz;
for (Re j = 1; j < siz; ++j)
{
if (pr[j][0] && pr[j][0] ^ pr[j + 1][0]) add(num + pr[j + 1][0], num + pr[j][0], 0);
if (pr[j][1] && pr[j][1] ^ pr[j + 1][1]) add(num + pr[j + 1][1], num + pr[j][1], 0);
if (pr[j][1] && nt[j + 1][0]) add(num + nt[j + 1][0], num + pr[j][1], lca(eg[a[j].s].w, eg[a[j + 1].s].w));
}
num += siz;
}
dij();
for (Re i = 1; i <= num; ++i) ans[id[i]] = min(ans[id[i]], dis[i]);
for (Re i = 2; i <= n; ++i) write(ans[i]);
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号