【论文阅读】From Word Embeddings To Document Distances
论文介绍的WMD(Word Mover's Distance)是一种基于词嵌入(word embedding)计算两个文本之间距离的方法。
本文跳过词嵌入的介绍,直接进入WMD的实现过程。
词的相似性
假设我们有一个包含$n$个词的词典库,用word2vec训练好的这$n$个词的矩阵为:
$$X \in R^{d*n} \tag{1}$$
矩阵$X$中的第$i$列,$x_i$是一个$d$维向量,表示第$i$个单词的词向量。
这样两个词之间的相似性可以通过词向量之间的欧氏距离(Euclidean distance)来表示:
$$c(i, j) = ||x_i - x_j||_2 \tag{2}$$
这里,第$i$个词和第$j$个词之间的相似性记为$c(i, j)$,即等于两者的词向量$x_i$和$x_j$之间的欧氏距离。
文本间距
对于一篇文本,我们可以用归一化的nBOW(normalized bag-of-words)向量$d$表示:
$$d = (d_1, d_2, \cdots, d_i, \cdots, d_n) \tag{3}$$
$$d_i = \frac{c_i}{\sum_{j=1}^{n} c_j}, \,\,\, i = 1, 2, \cdots, n \tag{4}$$
这里的$c_i$表示第$i$个词在文本出现的次数,统计所有词的出现次数,我们可以计算出每个词出现的比率$d_i, \,\,\, i = 1, 2, \cdots, n$。
现在有两篇文本,它们的nBOW表示分别为$d$和$d'$。
对于文本之间的距离度量,我们先定义一个矩阵$T \in R^{n*n}$,按照我自己的理解,矩阵$T$中一项$T_{ij} \geq 0$按是$d$中的第$i$个词有多大的可能转换到$d'$中的第$j$个词(原文: Let $T ∈ R^{n×n}$ be a (sparse) flow matrix where $T_{ij} ≥ 0$ denotes how much of word $i$ in $d$ travels to word $j$ in $d'$)。
为了使$d$全部翻译成$d'$,需要满足一下条件,输出流$\sum_j T_{ij} = d_i$,输入流$\sum_i T_{ij} = d_j'$
我们可以这样定义两个文本之间的距离:$d$中的每一个词与$d'$中的每一个词的之间的相似性的加权和,即
$$\sum_{i,j} T_{ij} c(i, j)$$
$\sum_{i,j} T_{ij} c(i, j)$的最小取值就是论文中给出的WMD(Word move distance)。
\begin{align*}
& \min_{T \geq 0} \sum_{i,j} T_{ij} c(i, j) \\
& s.t. \,\,\,\,\,\, \sum_{j=1}^n T_{ij} = d_i \,\, \forall i \in \{1, \cdots, n\} \\
& \sum_{i=1}^n T_{ij} = d_j' \,\, \forall j \in \{1, \cdots, n\} \tag{5}
\end{align*}
快速计算文本间距
理论上,由于WMD的最优问题的时间复杂度是$O(p^3 log p)$,这里$p$表示$d$中有多个词,重复不计。
因为对计算大文本间的WMD需要的时间是非常大,所以,有必要采取一些trick,近似得到我们要计算的目标。
WCD
我们知道,一个文本$d$可以用nBOW向量表示,$d = (d_1, d_2, \cdots, d_i, \cdots, d_n)$,向量中的第$i$个词可以用词库中第$i$个词在这个文本中出现次数与文本总词数(去除停用词)之比。
由word2vec得到词向量矩阵$X = (x_1, x_2, \cdots, x_i, \cdots, x_n)$,其中$x_i$表示词库中第$i$个词的词向量。
那么$d_i * x_i$表示这个本文中第i个词的词向量的加权($d_i$)表示。
所以,文本$d$可以用向量$Xd = \sum_i d_i x_i$表示。
定义$||Xd - Xd'||_2$为两个文本的WCD(Word centroid distance)。
由三角形不等式知,对于$p-norm$(p范数)有
$${||x||}_p = {(\sum_{i=1}^n {|x_i|}^p)}^{1/p} \tag{6}$$
当$p=2$时,$2-norm$表示的是欧氏距离。
对于WMD,我们有
\begin{align*}
\sum_{i=1, j=1}^n T_{ij} c(i,j)
&= \sum_{i=1, j=1}^n T_{ij} {||x_i - x_j'||}_2 \\
&= \sum_{i=1, j=1}^n {||T_{ij}(x_i - x_j')||}_2 \\
&\geq {||\sum_{i=1, j=1}^n T_{ij}(x_i - x_j')||}_2 \\
&= {||\sum_{i=1}^n {(\sum_{j=1}^n T_{ij}) x_i} - \sum_{j=1}^n {(\sum_{i=1}^n T_{ij}) x_j}||}_2 \\
&= {||\sum_{i=1}^n {d_i x_i} - \sum_{j=1}^n {d_j' x_j'}||}_2 \\
&= {||Xd - Xd'||}_2 \tag{7}
\end{align*}
所以,WCD是WMD的一个下界,时间复杂度是$O(dp)$,我们可以通过快速计算WCD近似得到WMD。
RWMD
为了进一步提升WMD的下界,我们可以通过下WMD计算的约束条件放宽松些,论文中给出的是放弃约束$\sum_{i=1}^n T_{ij} = d_j' \,\,\, \forall i \in \{1, \cdots, n\}$
同时定义$T_{ij}^{\ast}$
$$T_{ij}^{\ast} = \begin{cases}
& d_i, \text{ if } j = argmin_j c(i,j) \\
& 0, \text{ otherwise }
\end{cases} \tag{8}$$
$$j^{\ast} = argmin_j c(i, j) \tag{9}$$
所以有
\begin{align*}
\sum_{i,j} T_{ij} c(i, j)
&\geq \sum_{j} T_{ij} c(i, j^{\ast}) \\
&= c(i, j^\ast ) \sum_{j} T_{ij} \\
&= c(i, j^\ast ) d_i \\
&= \sum_j T_{ij}^{\ast} c(i, j) \tag{10}
\end{align*}
Prefetch and prune
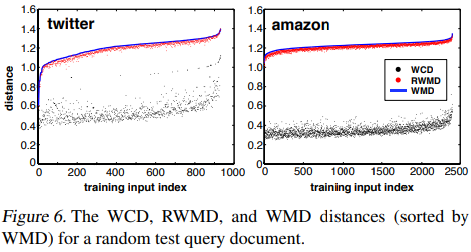
这样我们就得到了WMD两个下界,WCD和RWMD。如下图,根据原文的随机测试的统计结果,我们看到RWMD比WCD更加接近WMD的值。
我们可以综合利用WCD,RWMD,WMD,查找给定文本在文本集中距离最近的k个文本时:
- 首先把文本集中文本按照它们到给定文本的WCD距离由小到大排序;
- 计算前k个文本的WMD距离,记第k近邻的文本的WMD为$d_{WMD}^k$;
- 对于文本集中剩下的每一个文本,计算其到给定文本的RWMD,记为$d_{RWMD}^i,i = k+1, k+2, \cdots$,如果$d_{RWMD}^i > d_{WMD}^k$,则把它剪除(pruned),否则,计算这个文本到给定文本的WMD距离,如果有需要,则用当前文本替换第k个最近邻文本(prefetch)。
原文指出,由于RWMD非常接近WMD的值,在一些数据集上,步骤$3$的通过计算RWMD距离,可以剪除95%的文本,大大节省了整个的查找时间。
代码实现
由式$(5)$知,WMD是一个带约束的线性规划问题(LP),下面给出简单实现WMD的代码。
### 准备工作,下载词向量文件--glove.6B.zip https://nlp.stanford.edu/projects/glove/
'''
scipy.optimize._linprog def linprog(c: int,
A_ub: Optional[int] = None,
b_ub: Optional[int] = None,
A_eq: Optional[int] = None,
b_eq: Optional[int] = None,
bounds: Optional[Iterable] = None,
method: Optional[str] = 'simplex',
callback: Optional[Callable] = None,
options: Optional[dict] = None) -> OptimizeResult
矩阵A:就是约束条件的系数(等号左边的系数)
矩阵B:就是约束条件的值(等号右边)
矩阵C:目标函数的系数值
'''
# 下载词向量文件glove.6B.zip https://nlp.stanford.edu/projects/glove/
from gensim.scripts.glove2word2vec import glove2word2vec
from gensim.models import KeyedVectors
from collections import defaultdict, Counter
from scipy import optimize as opt
import numpy as np
# 读取Glove文件,这里使用维度为100的词向量。
def load_embedding():
glovefile = "glove.6B.100d.txt"
word2vecfile = "word2vec.txt"
with open(glovefile, 'r', encoding = 'utf-8') as f:
texts = f.readlines()
token2id = defaultdict(lambda: -1)
texts = [txt.split() for txt in texts]
tokens = [txt[0] for txt in texts]
embeddings = [txt[1:] for txt in texts]
for i, t in enumerate(tokens):
token2id[t] = i
embedding_mat = np.array(embeddings).astype(float)
# print(embedding_mat.shape)
return embedding_mat, token2id
# 计算文本间的WMD
def WMD(sent1, sent2, embedding_mat, token2id):
# 预处理文本,获取文本的nBOW表示
n, _ = embedding_mat.shape
s1 = list(map(lambda x: x.lower(), sent1.split()))
s2 = list(map(lambda x: x.lower(), sent2.split()))
c = Counter(s1)
d1 = np.array([0.0 for i in range(n)])
for k, v in c.items():
d1[token2id[k]] = float(v)
d1 = d1 / d1.sum()
c = Counter(s2)
d2 = np.array([0.0 for i in range(n)])
for k, v in c.items():
d2[token2id[k]] = float(v)
d2 = d2 / d2.sum()
# 计算向量之差的2-norm作为向量间的距离
def get_2norm_distance(x1, x2):
s = x1 - x2
dist = np.linalg.norm(s, ord = 2)
return dist
s1 = list(set(s1))
s2 = list(set(s2))
# 定义T_ij的系数向量
n, m = len(s1), len(s2)
T = np.array([0.0 for _ in range(n*m)])
for i in range(n * m):
T[i] = get_2norm_distance(embedding_mat[token2id[s1[int(i / m)]]], embedding_mat[token2id[s2[int(i % m)]]])
# 定义等式约束的左边系数矩阵
a1 = np.ones((n, m))
t1 = np.zeros((n * n * m)).reshape(n, -1)
for i in range(n):
for j in range(m):
t1[i, i * m + j] = a1[i][j]
a2 = np.ones((m, n))
t2 = np.zeros((m * n * m)).reshape(m, -1)
for i in range(m):
for j in range(n):
t2[i, j * m + i] = a2[i][j]
a = np.vstack((t1, t2))
# 定义等式约束的右边
const1 = np.array([d1[token2id[c]] for c in s1])
const2 = np.array([d2[token2id[c]] for c in s2])
b = np.hstack((const1, const2))
lim = (0, None)
bounds = tuple([lim for _ in range(n * m)])
res = opt.linprog(T, None, None, a, b, bounds = bounds)
wmd_dist = np.dot(T, res["x"])
return wmd_dist
if __name__ == '__main__':
s1 = "Obama speaks to the media in Illinois"
s2 = "The President greets the press in Chicago"
s3 = "The band gave a concert in Japan"
embedding_mat, token2id = load_embedding()
print('The WMD between s1 and s2 is: ', WMD(s1, s2, embedding_mat, token2id))
print('The WMD between s1 and s3 is: ', WMD(s1, s3, embedding_mat, token2id))
运行结果
The WMD between s1 and s2 is: 3.4892724527705172 The WMD between s1 and s3 is: 4.544411509507881

 浙公网安备 33010602011771号
浙公网安备 33010602011771号