置换矩阵 摘自维基百科
置换矩阵
在数学中的矩阵论里,置换矩阵是一种系数只由0和1组成的方块矩阵。置换矩阵的每一行和每一列都恰好有一个1,其余的系数都是0。在线性代数中,每个n阶的置换矩阵都代表了一个对n个元素(n维空间的基)的置换。当一个矩阵乘上一个置换矩阵时,所得到的是原来矩阵的横行(置换矩阵在左)或纵列(置换矩阵在右)经过置换后得到的矩阵。
目录
严格定义[编辑]
每个n元置换都对应着唯一的一个置换矩阵。设π 为一个n元置换:
给出其映射图:
它对应的n × n的置换矩阵Pπ是:在第i横行只有π(i)位置上系数为1,其余为0。即可以写做:
其中每个 表示正则基中的第j个,也就是一个左起第j个元素为1,其余都是0的n元横排数组。
表示正则基中的第j个,也就是一个左起第j个元素为1,其余都是0的n元横排数组。
由于单位矩阵是
置换矩阵也可以定义为单位矩阵的某些行和列交换后得到的矩阵。
性质[编辑]
对两个n元置换π 和 σ的置换矩阵Pπ 和Pσ,有
一个置换矩阵Pπ 必然是正交矩阵(即满足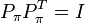 ),并且它的逆也是置换矩阵:
),并且它的逆也是置换矩阵:
用置换矩阵 左乘一个列向量 g所得到的是 g 的系数经过置换后的向量:
左乘一个列向量 g所得到的是 g 的系数经过置换后的向量:
用置换矩阵 右乘一个行向量 h 所得到的是 h 的系数经过置换后的向量:
右乘一个行向量 h 所得到的是 h 的系数经过置换后的向量:
置换矩阵与置换[编辑]
设Sn是n次对称群,由于n置换一共有n! 个,n阶的置换矩阵也有n! 个。这n! 个置换矩阵构成一个关于矩阵乘法的群。这个群的单位元就是单位矩阵。设A是所有n阶的置换矩阵的集合。映射Sn → A ⊂ GL(n, Z2)是一个群的忠实表示。
对一个置换σ,其对应的置换矩阵Pσ是将单位矩阵的横行进行 σ 置换,或者将单位矩阵的横行进行 σ−1 置换得到的矩阵。
置换矩阵是双随机矩阵的一种。伯克霍夫-冯·诺伊曼定理说明每个双随机矩阵都是同阶的置换矩阵的凸组合,并且所有的置换矩阵构成了双随机矩阵集合的所有端点。
置换矩阵Pσ的迹数等于相应置换σ的不动点的个数。设 a1、a2、……、ak 为其不动点的序号,则ea1、ea2、……、eak 是Pσ的特征向量。
由群论可以知道,每个置换都可以写成若干个对换的复合。由此可知,置换矩阵Pσ都可以写成若干个表示两行交换的初等矩阵的乘积。Pσ的行列式就等于 σ 的符号差。
例子[编辑]
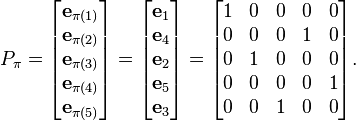
对应于置换π = (1 4 2 5 3)的置换矩阵Pπ 是
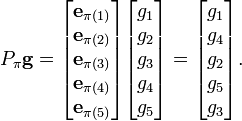
给定一个向量 g,
推广[编辑]
置换矩阵概念的一个推广是将方阵的情况推广到一般矩阵的情况:
- 一个m×n的0-1矩阵 P 是置换矩阵当且仅当
![P \cdot P^T = I_m]()
这时一个0-1矩阵是置换矩阵当且仅当它的每一行恰有一个1,每一列至多有一个1。
置换矩阵概念的另一个推广是将每行的1变为一个非零的实数:
- 一个n阶的方块矩阵 P 是置换矩阵当且仅当其每一行与每一列都恰好只有一个系数不为零。
这时的置换矩阵P可以看做由0和1组成的置换矩阵Q与一个对角矩阵相乘的结果。
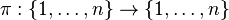


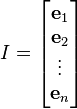
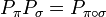

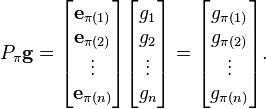
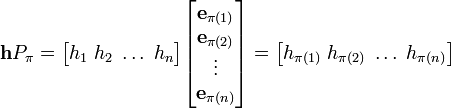
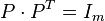

 浙公网安备 33010602011771号
浙公网安备 33010602011771号