它们其实都是图(二分图)

参考《挑战程序设计竞赛》

https://www.cnblogs.com/Ymir-TaoMee/p/9448406.html

二分图判定

• 问题描述：给定一个具有n个顶点的图，要对图上每个顶点染色，并且要使相邻的顶点颜色不同，问是否能最多用2种颜色进行染色。题目保证没有重边和自环。

• 分析：
  科普：把相邻点染成不同颜色的问题叫做图着色问题。对图进行染色所需要的最小颜色称为最小着色数。最小着色数是2的图称作二分图。
  如果只用2种颜色，那么确定一个顶点的颜色之后，和它相邻的顶点的颜色也就确定了。因此可以用dfs进行遍历，选择任意一个顶点出发，依次确定相邻顶点的颜色，就可以判断是否可以被2种颜色染色了。

 c++解法：

// 一个简单的二分图的判断
 
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
 
const int MAX_N =105;
int V,E;
// 使用邻接表模拟一张无向图
vector<int> G[MAX_N];
// 顶点的颜色,初始化为0，上色有两种颜色（0 or 1）
int color[MAX_N];
 
bool dfs(int v, int c)
{
    color[v] = c;       // 把顶点染成c
    for(int i = 0; i < G[v].size(); i++)
    {
        // 如果当前点的相邻的点同色就返回false
        if(color[G[v][i]] == c)
            return false;
        // 如果当前点的邻点还没被染色，就染成-c
        if(color[G[v][i]] == 0 && !dfs(G[v][i], -c))
            return false;
    }
    // 如果当前点都被染过色，就返回true
    return true;
}
 
void solve()
{
    for(int i = 0; i < V; i++)
    {
        if(color[i] == 0)
        {
            if(!dfs(i,1))
            {
                cout << "no" << endl;
                return;
            }
        }
    }
    cout << "yes" << endl;
}
 
int main()
{
    cin >> V >> E;
    for(int i = 0; i < E;  i++)
    {
        int s, t;
        cin >> s >> t;
        G[s].push_back(t);
        G[t].push_back(s);  // 如果有向图则无需这一句
    }
    memset(color, 0, sizeof(color));
    solve();
 
    return 0;
}

Java解法：

package graph;

import java.util.ArrayList;
import java.util.Scanner;


public class Main {
	static int MAX_V=10000;
	static ArrayList<Integer> G[]=new ArrayList[MAX_V];//邻接表存图
	static int color[]=new int[MAX_V];//顶点的颜色1或-1

	 //把顶点染成1或-1
	static boolean dfs(int v, int c)
	{
		color[v]=c;//把顶点v染成颜色c
		for (int i=0; i<G[v].size(); i++)
		{
			//如果相邻顶点同色，则返回false
			if (color[G[v].get(i)]==c) return false;
			//如果相邻顶点还没被染色，则染成-c
			if (color[G[v].get(i)]==0 && !dfs(G[v].get(i),-c)) return false;//
		}
		//如果所有顶点都染过色了，则返回true
		return true;
	}
	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		int V,E;
		V=sc.nextInt();
		E=sc.nextInt();
		for (int i = 0; i < MAX_V; i++) {
			G[i]=new ArrayList<>();
		}
		for (int i = 0; i < E; i++) {
			int s=sc.nextInt();
			int t=sc.nextInt();
//			G[s]=new ArrayList<>(); 不能这样写 这样会重复初始化
//			G[t]=new ArrayList<>();
			G[s].add(t);
			G[t].add(s);
		}
		for (int i=0; i<V; i++)
		{
			if (color[i]==0)
			{
				if (!dfs(i,1))//如果顶点还没被染色，则染成1
				{
					System.out.printf("No\n");
					return;
				}
			}
		}
		System.out.printf("Yes\n");
	}

}

二分图的最大匹配(匈牙利算法)

二分图的定义

如果一个图的所有顶点可以被分为X和Y两个集合，并且所有边的两个顶点恰好一个属于集合X，另一个属于Y，即每个集合内的顶点没有边相连，那么此图就是二分图。

例图：

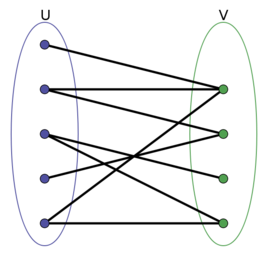
增广路

找到一条增广路就是使得二分图的配对数加一，增广路的本质是一条路径的起点和终点都是未被配对的点。

最大匹配

在当前匹配方案下再也找不到增广路，那么当前匹配就是最大匹配。

匈牙利算法

  我们来看图二,可以知道了这个二分图各点之间的联系.那么该算法如何实现最大匹配呢.

  根据字典序,显然易见,我们可以知道,A->E.
  随后,我们看B点,它要连E,但是E被占用了,我们该怎么办?我们把A->E之间的边暂时去掉,变成黄色,然后让B->E链接,但是A不能没有,于是这里从A再走,E不行,但是有个F.所以A->F.


  于是C->G也按此法加上,轮到D,我们发现G已经被连了.怎么办?将C->G的边暂时去掉.再从C走,看是否可以找别的边.但是我们发现,C只有到G的一条边.所以C->G保留,D只能孤立一人,我们无能为力.

算法

1、首先从任意一个未被配对的点u开始，从点u的边中任意选一条边（假设这条边是u->v）开始配对。如果此时点v还没有被配对，则配对成功，此时便找到一条增广路。此时若点v已经被配对了，那就要尝试进行“回溯”。若尝试成功，则找到一条增广路，此时需要更新原来的配对关系。这里需要一个数组match来记录配对关系，比如点v与点u配对了，就记作match[v]=u和match[u]=v。配对成功后，配对数加一。

2、若刚才所选的边配对失败，要从点u的边中再重新选一条边，进行尝试。直到点u配对成功，或者尝试过点u所有的边为止。

3、接下来继续对剩下没有被配对的点一一进行配对，直到所有的点都尝试完毕，找不到新的增广路为止。

4、输出配对数。
举一个例子：

男1 2 3 号，女1 2 3 号 去做过山车。可是，过山车的每一排只有两个座位，为了安全起见，每个女生必须与一名男生同坐。但是，每个女孩都希望和自己认识的人一组，女1只认识男1和男2，女2认识男2和男3，女3认识男1，你可以帮忙算算哪种组合可以坐上过山车吗？

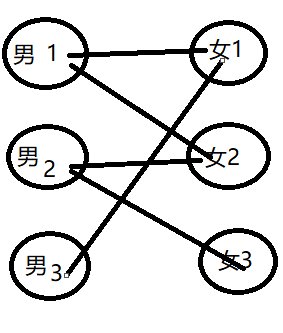
我们可以这么想,首先从左边的第1号女生开始考虑。先让她与1号男生配对,配对成功后,紧接着考虑2号女生。2号女生可以与2号男生配对,接下来继续考虑3号女生。此时我们发现3号女生只能和1号男生配对,可是1号男生已经配给1号女生了,怎么办?
此时3号女生硬着头皮走到了1号男生面前,貌似1号男生已经看出了3号女生的来意,这个时候1号男生对3号女生说:“我之前已经答应了与1号女生坐一起,你稍等一下,我让号女生去问问看她能否与其他认识的男生坐一起,如果她找到了别的男生,那我就和你坐一起。”接下来,1号女生便尝试去找别的男生啦。
此时1号女生来到了2号男生面前问:“我可以和你坐在一起吗?”2号男生说:“我刚答应和2号女生坐一起,你稍等一下,我让2号女生去问问看她能否与其他认识的男生坐起,如果她找到了别的男生,那我就和你坐一起。”接下来,2号女生又去尝试找别的男生啦。此时,2号女生来到了3号男生面前问:“我可以和你坐一起吗?”3号男生说:“我正 空着呢,当然可以啦!”此时2号女生回过头对2号男生说:“我和别的人坐在一起啦。”然 后2号男生对1号女生说:“现在我可以和你坐在一起啦。”接着,1号女生又对1号男生说 “我找到别的男生啦。”最后1号男生回复了3号女生:“我现在可以和你坐在一起啦。”

最终的结果就是：

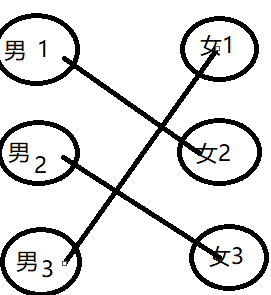
真足波折啊〜〜是不是有点连锁反应的感觉。最终通过这种连锁反应，配对数从原来的2 对变成了3对，增加了 1对。刚才的过程有个专业名词叫做增广路，不难发现如果找到一条增 广路，那么配对数将会加1。增广路的本质就是一条路径的起点和终点都是末被配对的点。 既然增广路的作用是“改进”匹配方案（增加配对数），如果我们己经找到—种匹配方 案，如何确定当前这个匹配方案已经是最大匹配了呢？如果在当前匹配方案下再也找不到增 广路，那么当前匹配就是最大匹配/,算法如下。

 

#include<stdio.h>
int e[100][100],match[100],book[100];
int n,m;
int dfs(int u)
{
    int i;
    for(i=1;i<=n;i++)
    {
        if(book[i]==0&&e[u][i]==1)
        {
            book[i]=1;
            if(match[i]==0||dfs(match[i]))
            {
                match[i]=u;
                match[u]=i;
                return 1;
            }
        }
    }
    return 0;
}
int main()
{
    int i,j,t1,t2,sum=0;
    scanf("%d %d",&n,&m);
    for(i=1;i<=m;i++)
    {
        scanf("%d%d",&t1,&t2);
        e[t1][t2]=1;
        e[t2][t1]=1;
    }
    for(i=1;i<=n;i++)
    match[i]=0;
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=n;j++)
        book[j]=0;
        if(dfs(i))
        sum++;
    }
    printf("%d",sum);
    return 0;
}