二叉树定义

树的定义
    树(Tree)是n(n>=0)个结点的有限集
    若 n=0,称为空树
    若 n>0,则它满足如下两个条件
        1：有且仅有一个特定的称为根(Root)的结点
        2：其余结点可分为m(m>=0)个互不相交的有限集T1,T2,...,Tm,
            其中每个集合本身又是一棵树，并称为根的  子树(SubTree)

树的术语
    图示1：

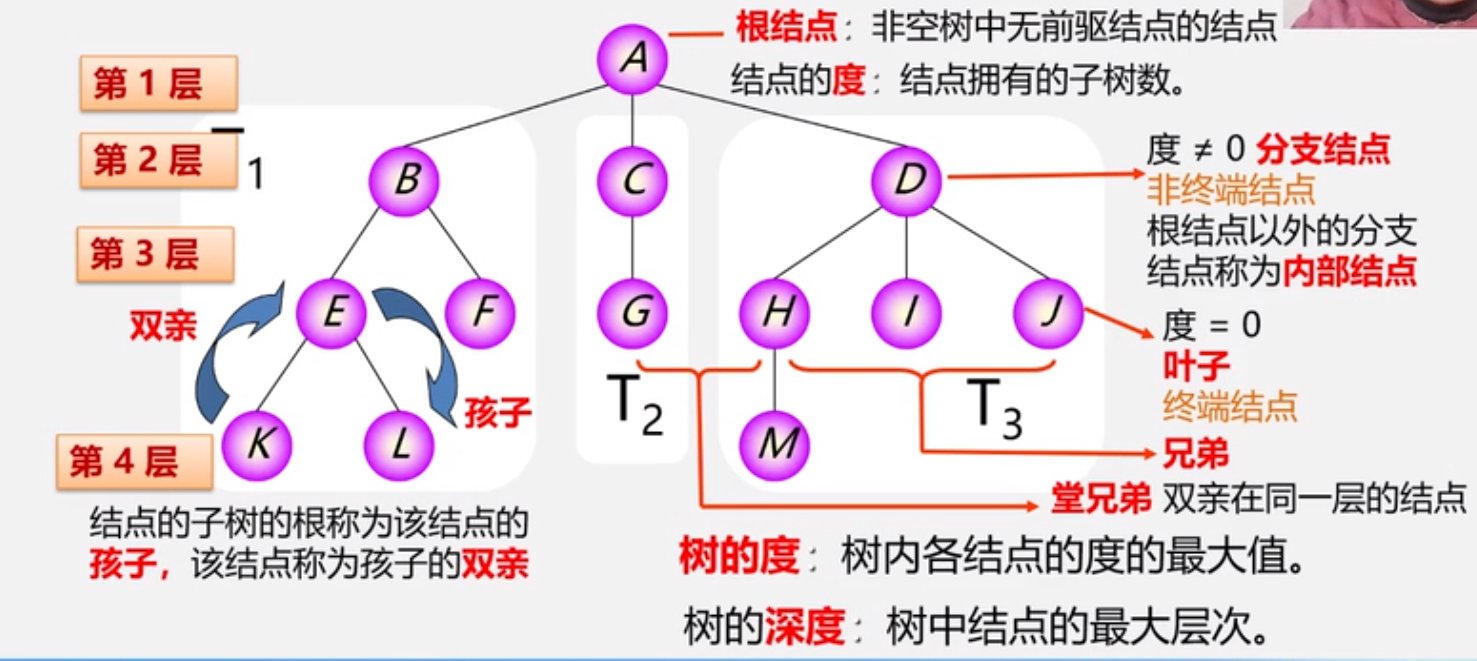    有序树：
        树中结点的各子树从左至右有次序（最左边为第一个孩子）
    无序树：
        树种结点的各子树无次序
    森林：
        m(m>=0)颗互不相交的树的集合
二叉树
    解释：
        为何要重点研究每结点最多只有两个“叉”的树？
            二叉树的结构最简单，规律性最强；
            可以证明，所有树度能转为唯一对应的二叉树，不失一般性
        普通树(多叉树)若不转化为二叉树，则运算很难实现
    定义：
        二叉树是n(n>=0)个结点的有限集，它或者是空集(n=0),或者由一个根结点及两颗互不相交的分别称为
        这个根的左子树和右子树的二叉树组成
    特点：
        1：每个结点最多有俩孩子（二叉树中不存在度大于2的结点）
        2：子树有左右之分，其次序不能颠倒
        3：二叉树可以是空集合，根可以有空的左子树和右子树
    注意：
        二叉树结点的子树要区分左子树和右子树，即使只有一颗子树也要进行区分
        ，要说明它是左子树，还是右子树

        树当结点只有一个孩子时，就无序区分它是左还是右的次序。因此，
        二者是不同的。这是二叉树与树的最主要的区别

        （也就是二叉树每个结点位置或者说次序都是固定的，可以是空，但是不
        可以说它没有位置，而树的结点位置是相对于别的结点来说的，没有别的
        结点时，它就无所谓左右了）

        虽然二叉树与树概念不同，但有关树的基本术语对二叉树都适用