C.L. 大一下周常训练报告
暂断更。
大一下的训练计划
「日常」 CF *2400 ~ *2700 泛做,AT *2300 ~ *2700 泛做,交互题泛做。
「日常」 参加 CF / AT ... 线上赛。
「周常」 vp 邀请赛 / 省赛 / CCPC(备战可能到来的 CCPC Final)。
「长期」 重构 OI+ACM 笔记。
「长期」 学习 C++ 进阶语法,学习 python。
第三周(2025.03.10 ~ 2025.03.16)
周一
CF 1253F(*2500)
若所有节点均为充电桩,则从 \(a\) 走到 \(b\) 的答案,即为 \(a, b\) 之间所有简单路径上最大边权的最小值。此时只需求出最小生成树,使用树上倍增求出 \(a, b\) 之间的最大边权即可。
记 \(\mathrm{dist}_u\) 表示 \(u\) 距离最近充电桩的距离,可以用多源点 dijkstra+heap 求出。
但正常情况下可能要经过非充电桩的节点。考虑一个贪心策略:每次走到一个节点的时候,都去距离它最近的一个充电桩补满电量再回来。
(因为走回充电桩至少需要花费 \(\mathrm{dist}_u\)。若此时电量小于 \(\mathrm{dist}_u\) 则走不回去,若此时电量大于等于 \(\mathrm{dist}_u\),则可以先花费 \(\mathrm{dist}_u\) 的电量走回去补满电量再回来,可以认为在 \(u\) 点时的电量为 \(c - \mathrm{dist}_u\))
由于起点与终点均为充电桩,则若要经过原图上的一条边 \((x, y, z)\),电池容量至少为 \(\mathrm{dist}_x + z + \mathrm{dist}_y\)(因为至少要从充电桩走到其中一个端点,经过这条边,再从另外一个端点走到充电桩)。
故对于每条边 \((x, y, z)\),使用 \(\mathrm{dist}_x + z + \mathrm{dist}_y\) 代替它的边权。此时从 \(a\) 走到 \(b\) 的答案,即为 \(a, b\) 之间所有简单路径上最大边权的最小值。
CF 1188C(*2500)
考虑先求出美丽值的上界,显然为 \(\frac{\max a_i}{k - 1}\)。
考虑对每个美丽值 \(v\),计算有多少长度为 \(k\) 的子序列的美丽值为 \(v\),记作 \(\mathrm{Count}(v)\)。但发现直接做不太好做,于是我们考虑计算有多少个长度为 \(k\) 的子序列的美丽值 \(\geq v\),记作 \(\mathrm{Count}(\geq v)\)。最后再使用 \(\mathrm{Count}(\geq v) - \mathrm{Count}(\geq v+1)\) 得到 \(\mathrm{Count}(v)\)。
(直接使用 \(\sum v \cdot \mathrm{Count}(v) = \sum_{v = 1}\mathrm{Count}(\geq v)\) 亦可)
将序列 \(a\) 从小到大排序。对于每个 \(v\),记 \(f(i, j)\) 表示考虑到了 \(a_1, \cdots, a_i\),子序列的最后一个数为 \(a_i\),包含 \(j\) 个数,且美丽值 \(\geq v\) 的子序列个数。显然有
该式子显然可以用前缀和 + 双指针优化。
时间复杂度 \(\mathcal{O}\left(nk \cdot \frac{\max a_i}{k}\right) = \mathcal{O}(n\max a_i)\)。1e8 过 5s 还是绰绰有余的。
CF 813F(*2500)
评分虚高 ...
离线加边、删边,很容易想到线段树分治。此题刚好可以回顾一下,使用扩展域并查集实现二分图判定。
扩展域并查集中的节点 \(x\) 表示 "节点 \(x\) 在二分图左部" 这一事件,节点 \(x + n\) 表示 "节点 \(x\) 在二分图右部" 这一事件。若并查集中的两个节点联通,则表示两个节点代表的事件,要么同时发生要么同时不发生。
对于原图中的每一条边 \((x, y)\),在并查集中连接 \((x, y + n)\) 以及 \((x + n, y)\)。
当存在一个节点 \(x\),满足 \(x\) 与 \(x + n\) 联通时,显然 \(x\) 不可能即在左部又在右部,故此时这张图不是二分图。
另一种理解方式:众所周知,一张图为二分图当且仅当该图存在奇环。
在扩展域并查集上,若一条路径长度为奇数,则起点与终点在异侧。故一张图存在奇环,当且仅当存在一个节点 \(x\),满足 \(x\) 与 \(x + n\) 联通。
注意,可撤销并查集使用的是按秩合并,按秩合并不能与路径压缩混用。
CF 1209E2(*2500)
首先,真正有效的列,一定在列最大值前 \(n\) 大的那些列之中。容易使用反证法证明。
考虑一列一列处理,在每一列中钦定有哪些位置为对应行的最大值。由于此题要求的是最大值之和的最大值,故在统计答案的过程中,我们不必保证每次钦定的最大值一定是真实的最大值。因为这样肯定不优。
设 \(f(j, S)\) 表示考虑到了前 \(j\) 列,其中每行的最大值确定状态为一个二进制数 \(S\)(若 \(S\) 的第 \(i\) 位为 \(1\),则表示第 \(i\) 行的最大值已经确定),则有
其中 \(\mathrm{value}(j, S)\) 表示第 \(j\) 列中,所有行号属于 \(S\) 的位置,在 \(0 \sim n - 1\) 次循环移位下的元素之和的最大值。
时间复杂度 \(\mathcal{O}(n3^n + n^22^n)\)。
CF 1527E(*2500)
评分虚高 ...
显然可以写一个很暴力的 dp。设 \(f(i, j)\) 表示考虑到了前 \(i\) 项,划分了 \(j\) 段时的最小代价,则有
直接做的时间复杂度 \(\mathcal{O}(n^2k)\) 的。
盲猜该 dp 具有决策单调性。此类代价 \(\mathrm{cost}(l, r)\) 难以计算的决策单调性优化问题,则可以考虑分治。使用类似莫队的方法处理 \(\mathrm{cost}(l, r)\)。
时间复杂度 \(\mathcal{O}(nk \log n)\)。
CF 580E(*2500)
评分虚高 ...
\(s\) 有长度为 \(r\) 的 border \(\iff\) \(|s| - r\) 是 \(s\) 的混循环节。故使用线段树维护子区间的哈希值即可。
特别要注意 \(d = r - l + 1\) 的情况,corner case 还需多加注意。
Codeforces Round 1008 (Div. 1)
A(*1500)
移项得 \(a_1 + a_3 + \cdots + a_{2n+1} = a_2 + a_4 + \cdots + a_{2n}\),即奇数位之和等于偶数位之和。
考虑最极端的构造,将最小的 \(n - 1\) 个数放在偶数位,将最大的 \(n + 1\) 个数放在奇数位,用偶数位的剩下一个位置补齐差值。
该差值等于最大的 \(n + 1\) 个数之和减去最小的 \(n - 1\) 个数之和,该差值显然比原来 \(2n\) 个数的最大值要大,故不会重复,构造符合题意。
(一开始还想反了,想成了将最小的 \(n\) 个数放在奇数位,最大的 \(n\) 个数放在偶数位,但此时最大值也参与了配对,显然可以被构造成重复)
B(*1900)
注意到要回答 \((m \mid x) + (m \mid y)\) 的值,只需知道 \(x, y\) 在二进制下的每一位上共有多少个 \(1\) 即可。
假设我们查询 \(0\) 得到了 \(x + y\) 的值,是不足以知道 \(x, y\) 在二进制下的具体情况的,究其原因是因为加法会导致进位,从而导致位与位之间不独立。
注意到单次进位时,位置的奇偶性一定会改变。故我们考虑在处理奇数位的信息时,屏蔽偶数位的贡献;在处理偶数位的信息时,屏蔽奇数位的贡献。故可以查询 ...010101 与 ...101010,此时就不会发生多次进位,做到了位与位之间的独立。
C(*2300)
注意到,若将字符 1 看成 \(+1\),将字符 0 看成 \(-1\),则 \(F(v, l, r)\) 即为区间 \([l, r]\) 的权值之和。
对于一个长度为 \(n\) 的字符串 \(v\),其贡献为
这是个二次函数的形式,显然 \(F(v, 1, i)\) 在 \(\left\lfloor \frac{F(v, 1, n)}{2} \right\rfloor\) 处取到最值,且前缀的 \(F\) 值一定构成一个连续的区间,故 \(\left\lfloor \frac{F(v, 1, n)}{2} \right\rfloor\) 一定可以取到。
记 \(\mathrm{value}(x) = \left\lfloor \frac{x}{2} \right\rfloor\left(x - \left\lfloor \frac{x}{2} \right\rfloor\right)\),则一个长度为 \(n\) 的字符串 \(v\) 的贡献为
注意到,一个字符串的权值仅和该字符串的 0 与 1 个数相关,字符的顺序是不重要的。
设 \(a\) 表示全局 1 的个数,则 \(n - a\) 表示全局 \(0\) 的个数,故子序列的权值 \(x\) 的取值范围为 \([a - n, a]\)。
对于一个权值 \(x\),考虑计算有多少个子序列的权值等于 \(x\),枚举子序列 1 的个数 \(i\),则 0 的个数为 \(i - x\)。
发现这是一个和 \(a\) 有关的卷积式,使用 NTT 即可。给 998244353 磕一个。
周二
CF 1559D2(*2500)
首先一条边 \((u, v)\) 能添加,当且仅当 \(u, v\) 在 \(G_1, G_2\) 中均不连通。
可以证明,不妨设 \(G_1\) 的连通块数多于 \(G_2\),则 \(G_2\) 最后的连通块数一定可以操作至 \(1\)(即合并成一棵树)。
证明:考虑最终状态,若 \(G_1\) 有多个连通块,任选两个连通块 \(A, B\),设 \(a \in A, b \in B\),则 \(a, b\) 在 \(G_2\) 中一定连通,故 \(A, B\) 中的节点在 \(G_2\) 中一定在同一个连通块中。对于 \(G_1\) 所有的联通块对进行相同的讨论,可知 \(G_2\) 已经形成了一棵树。
由于 \(G_2\) 一定会形成一棵树,故加边顺序是无关紧要的。
考虑优化这个贪心过程。先尽可能多地加入形如 \((1, x)\) 的边,此时所有节点至少在一个图中与 \(1\) 在同一个连通块中。所有的点 \(x\) 一定可以被分成三类:
- 在 \(G_1\) 中与 \(1\) 连通,在 \(G_2\) 中与 \(1\) 连通。
- 在 \(G_1\) 中与 \(1\) 连通,在 \(G_2\) 中与 \(1\) 不连通。
- 在 \(G_1\) 中与 \(1\) 不连通,在 \(G_2\) 中与 \(1\) 连通。
注意到 \((u, v)\) 能添加,当且仅当其中一个点为 \(2\) 类点,另外一个点为 \(3\) 类点。将 \(2\) 类点与 \(3\) 类点依次配对连边即可。
特别要注意连边的过程中可能会使得原来的 \(2, 3\) 类点变成 \(1\) 类点,于是我们每找到一个 \(2\) 类点或 \(3\) 类点 \(x\),就令 \(x\) 在对应图中与 \(1\) 连通,即可处理连边对 \(2, 3\) 类点的影响。
CF 484E(*2500)
评分虚高 ...
考虑二分答案,记 \(\geq \mathrm{mid}\) 的数为 \(1\),\(< \mathrm{mid}\) 的数为 \(0\),则一个区间 \([l, r]\) 合法当且仅当区间 \([l, r]\) 存在长度 \(\geq k\) 的全 \(1\) 连续段。
对 \(\{h_i\}\) 进行离散化,以值域为版本号,使用主席树维护区间最长全 \(1\) 连续段即可。
CF 875F(*2500)
考虑将王子抽象成点,将公主抽象成边。对于一个公主,设其备选的两个王子为 \(x, y\),需要的嫁妆为 \(z\)。考虑连一条无向边 \((x, y, z)\)。
一条边需要和这条边的一个端点配对,一个端点只能与与其相连的一条边配对。可以理解为每个节点至多选择一条出边,故选出的每个连通块要么是树、要么是基环树。故本题要求的是最大生成基环树森林。
考虑 Kruskal,对于一条边 \((x, y, z)\),当且仅当以下情况可以加入
- \(x, y\) 不连通,且 \(x, y\) 所在的连通块不能均为基环树。
- \(x, y\) 连通,且所在的连通块不为基环树(加入这条边之后,所在的连通块变为基环树)。
使用并查集维护连通性,再额外记录一个连通块是否为基环树即可。
Codeforces Round 1009 (Div. 3)
A(*800)
当且仅当 \(l = r = d = u\) 时,组成一个正方形。
一个四边形为正方形,当且仅当该四边形即为菱形,也为矩形。菱形可推出 \(l = r, d = u\),矩形可推出 \(l = u\)。故 \(l = r = d = u\)。
B(*800)
若 \(a, b, x\) 可以构成一个非退化三角形,则 \(x\) 满足 \(|a - b| < x < a + b\)。
故对于任意两个元素 \(a_i, a_j\),我们总贪心地选择 \(x = a_i + a_j - 1\)。总共进行 \(n - 1\) 次操作,故答案为 \(\sum_{i = 1}^n a_i - (n - 1)\)。
C(*1100)
显然 \(|x - y| \leq x \bigoplus y \leq x + y\)。
左侧取等当且仅当,其中一个数在二进制下为另一个数的子集。
右侧取等当且仅当,两个数在二进制下无交集。
此题还要注意到 \(y < x\) 的条件(因为这个条件 WA on test 1 两次)。
无解有两种情况:
- \(x\) 的第 \(0\) 位到最高位均为 \(1\)。
- \(x\) 只有最高位为 \(1\)。
否则设 \(x\) 的最高位为 \(h\),设 \(x\) 的第一个 \(0\) 位为 \(a\)。将 \(x\) 的第 \(h\) 位与第 \(a\) 位取反作为 \(y\),即可避免两种取等的情况。
D(*1400)
考虑计算 \(y\) 固定时,有多少的 \(x\) 处于圆内。对于每个圆,可以计算出 \(x\) 合法的一段区间。将若干个区间进行合并即可。时间复杂度 \(\mathcal{O}(\sum r_i \log \sum r_i)\)。
亦可计算 \(x\) 固定时,有多少的 \(y\) 处于圆内。对于每个 \(x\) 只需取 \(y\) 的最大值即可。
E(*1600)
考虑随机化。设 \(x, y, z\) 初始为 \(1, 2, 3\),每次都查询 \(x, y, z\),设查询结果为 \(p\):
- 若 \(p = 0\),则 \(x, y, z\) 即为答案;
- 若 \(p \neq 0\),则从 \(x, y, z\) 中等概率挑一个数替换为 \(p\)。
每次有 \(\frac{1}{3}\) 的概率,使得点数变为原来的 \(\frac{1}{3}\)。
F(*2000)
设 \(I_x, I_y\) 分别表示矩阵在 \(x, y\) 轴上的线段树区间。
设 \(a \in I_x, b \in I_y\),对于矩形 \(a \times b\):
- 边长 \(> \min(a, b)\) 的节点,都无法在不覆盖其他区域的前提下,覆盖该矩形。
- 边长 \(\leq \min(a, b)\) 的节点,要么完全在矩形内,要么完全在矩形外。
- 由于 \(a, b\) 都是 \(2\) 的若干次幂,我们可以使用 \(\frac{\max(a, b)}{\min(a, b)}\) 个边长为 \(\min(a, b)\) 的节点覆盖该矩形。
时间复杂度 \(\mathcal{O}(\log^2 X)\)。
G(*2100)
注意到一旦 \(i, j, k\) 三个点被选成一个三角形,则其他三角形不可以跨过 \(i, j, k\) 中的任意一个点。
考虑区间 dp,设 \(f(l, r)\) 表示考虑了顶点 \(l, \cdots, r\) 时的答案。有两种转移
时间复杂度 \(\mathcal{O}(n^3)\)。
特别要注意的是,虽然题目给出的是一个环,但却不必断环为链。
周三
CF 1313D(*2500)
注意到 \(m\) 是 \(10^9\) 级别,\(n\) 是 \(10^5\) 级别,有效的区间个数不会超过 \(2n + 1\) 个。于是可以考虑一个段一个段地进行 dp。
注意到 \(k\) 非常小,考虑状态压缩,使用一个二进制数表示当前段的区间选取情况。在 dp 的过程中动态地分配每个区间的编号。
CF 739C(*2500)
评分虚高 ...
容易想到使用线段树维护,问题是如何合并两个区间。简单推理可知,需要维护:
- \(\mathrm{sze}\):区间长度。
- \(\mathrm{lv}, \mathrm{rv}\):区间左端点的值,区间右端点的值。
- \(\mathrm{pre}\):区间前缀最长下降段。
- \(\mathrm{suf}\):区间后缀最长下降段。
- \(\mathrm{preans}\):区间中作为前缀的答案。
- \(\mathrm{sufans}\):区间中最为后缀的答案。
- \(\mathrm{ans}\):区间的答案。
简单讨论即可完成合并。
CF 594D(*2500)
注意到,对于一个质数 \(p\),若 \(p\) 是区间 \([l, r]\) 中某个数的因数,则欧拉函数还要再乘上 \(\frac{p - 1}{p}\)。而 \(10^6\) 以内,一个数最多只有 \(7\) 个质因数。于是我们要数出区间 \([l, r]\) 中作为约数出现的质数 \(p\) 所带来的影响。
一开始写了一个简单的莫队,可惜 TLE 了。
考虑扫描线,将所有的询问 \(l, r\) 按照右端点 \(r\) 从小到大排序。
对于一个质数 \(p\),设其在区间 \([1, r]\) 中最后一个作为因数出现的位置为 \(x\),则只要左端点 \(l \leq x\),答案就需要乘上 \(\frac{p - 1}{p}\)。
于是我们将 \(\frac{p - 1}{p}\) 的贡献挂在位置 \(x\) 处,询问区间 \([l, r]\) 只需求出区间 \([l, r]\) 的贡献之积即可。使用树状数组维护(树状数组也是可以求前缀积的)。
CF 704B(*2500)
连续段 dp 的一个好题。
注意到,当相邻两个数 \(i, j\) 的贡献是独立的,只取决于他们之间的大小关系。这有助于我们进行代价提前计算。
考虑从小到大加数。不可当成仅一个连续段处理的原因是,插入一个数会破坏原有的相邻大小关系,使得无法计算代价。
于是考虑连续段 dp,设 \(f(i, j)\) 表示填了 \(1 \sim i\),形成了 \(j\) 个连续段时的最小代价。大体上有四种转移:
- 将 \(i\) 独自新开一个连续段:此时 \(i\) 比两边都小。
- 将 \(i\) 接在某个连续段的左边:此时 \(i\) 比左小,比右大。
- 将 \(i\) 接在某个连续段的右边:此时 \(i\) 比左大,比右小。
- 通过 \(i\) 将某两个连续段合并:此时 \(i\) 比两边都大。
特别地,在 \(s, e\) 的影响下,某些情况下某些转移是不合法的。
周四
CF 825G(*2500)
此题相当于是要维护黑点点集 \(S\) 的最小联通子图的节点编号最小值。
在此题中,黑点不会再重新变回白点。考虑以任意一个黑点为根节点 \(\mathrm{root}\)(不妨定为第一次修改的黑点),通过一次 dfs 求出根节点到每个节点 \(x\) 的路径上,节点编号的最小值 \(\mathrm{dat}[x]\)。
每次新加入一个黑点 \(x\),就将 \(x\) 到 \(\mathrm{root}\) 路径上的所有点全都加入最小联通子图中(即用 \(\mathrm{dat}[x]\) 更新答案),显然任意两个黑点之间的所有点均被加入最小联通子图,故该种处理方式是正确的。且由于最小值具有可重复贡献性,故不用考虑去重。
2022 Shanghai Collegiate Programming Contest
咕咕咕 ...
周五
Luogu P4514(提高+/省选-)
对差分技巧的一个小回顾。
「知识点」一维差分:记 \(b_i = a_i - a_{i - 1}\),则 \(a_i = \sum_{j = 1}^i b_j\)。
「模型」区间修改 + 单点查询:若区间 \([l, r]\) 加上 \(x\),考虑差分数组的变化,有
使用树状数组维护 \(b_i\) 即可。
「模型」区间查询 + 区间查询:将区间查询拆成两个前缀做差的形式,考虑将前缀和使用差分数组表示
使用树状数组维护 \(b_i\),\(b_i \cdot i\) 即可。
「知识点」二维差分:记 \(b_{i, j} = a_{i, j} - a_{i - 1, j} - a_{i, j - 1} + a_{i - 1, j - 1}\),则 \(a_{i, j} = \sum_{x = 1}^i\sum_{y = 1}^j b_{x, y}\)。
「模型」矩阵修改 + 单点查询:若左上为 \((x_1, y_1)\) 右下为 \((x_2, y_2)\) 的矩阵加上 \(k\),考虑差分数组的变化,有
使用二维树状数组维护 \(b_{i, j}\) 即可。
「模型」矩阵修改 + 矩阵查询:将矩阵查询拆成四个前缀做差的形式,考虑将前缀和使用差分数组表示
使用二维树状数组维护 \(b_{i, j}\),\(b_{i, j} \cdot j\),\(b_{i, j} \cdot i\),\(b_{i, j} \cdot i \cdot j\) 即可。
CF 341D(*2500)
矩阵异或,矩阵查询异或和。
直接使用「模型」矩阵修改 + 矩阵查询的 Trick 即可,但此时乘法需要特殊处理(奇数个 \(x\) 异或为 \(x\),偶数个 \(x\) 异或为 \(0\))。
周六
CF 1174E(*2500)
本质不同的前缀 gcd 是 \(\mathcal{O}(\log n)\) 级别的,因为当前缀 gcd 改变时,新的 gcd 一定为旧的 gcd 的约数。
考虑在唯一分解角度下观察 gcd,设 gcd 为 \(\sum p_i^{c_i}\),为了使得本质不同的前缀 gcd 最多,当 gcd 变化时,肯定是选择某一个 \(c_i \gets c_i -1\)。
故为了使得本质不同的 gcd 最多,就是要使得排列的第一个数的 \(\sum c_i\) 最多。
首先,肯定不会存在质因子 \(p_i \geq 5\),因为此时可以将 \(p_i\) 换成 \(2^2\),\(\sum c_i\) 更大且仍然合法。
其次,肯定不会存在 \(3\) 的次数 \(\geq 2\),因为此时可以将 \(3^2\) 换成 \(2^3\),\(\sum c_i\) 更大且仍然合法。
故第一个数只能被表示成 \(2^x3^y\),其中 \(y \in \{0, 1\}\)。状态数为 \(\mathcal{O}(\log n)\)。
设 \(f(i, x, y)\) 表示,填到排列的前 \(i\) 位,且当前的 gcd 为 \(2^x3^y\) 时的方案数。设 \(\mathrm{calc}(x) = \left\lfloor \frac{n}{x} \right\rfloor\) 表示 \(1, \cdots, n\) 中 \(x\) 的倍数的个数。
初态:记 \(u = \lfloor \log_2 n \rfloor\),则有 \(f(1, u, 0) = 1\);若 \(2^{u - 1}3 \leq n\) 时,还有 \(f(1, u - 1, 1) = 1\)。
终态:\(f(n, 0, 0)\)。
CF 992E(*2500)
注意到 \(a_i \geq 0\)。若 \(a_i = s_{i - 1}\),则 \(s_i = 2s_{i - 1}\)。故满足要求的位置个数为 \(\mathcal{O}(\log a)\) 级别的。
进一步,可以考虑 \(a_i \geq s_{i - 1}\) 即 \(s_i \geq 2s_{i - 1}\)。满足该要求的位置个数也是 \(\mathcal{O}(\log a)\) 级别的。
故考虑使用线段树维护 \(a_i - s_{i - 1}\) 的最大值。每次暴力地遍历整棵线段树,遇到区间最大值 \(< 0\) 的区间就返回,遇到一个叶子就判断该点对应的 \(a_i - s_{i - 1}\) 是否为 \(0\)。
时间复杂度 \(\mathcal{O}(n \log n \log a)\)。
CF 1097F(*2500)
注意到 \(v \leq 7000\) 很小。设 \(a[x][v]\) 表示集合 \(x\) 中,\(v\) 的倍数的出现次数 mod 2 的值。使用 std::bitset 来维护 \(a[x]\)。
-
1 x v:枚举 \(x\) 的因数更新 \(a[x]\) 即可。 -
2 x y z:\(a[x] \gets a[y] \mathbin{\mathrm{and}} a[z]\)。 -
3 x y z:\(a[x] \gets a[y] \mathbin{\mathrm{xor}} a[z]\)。 -
4 x v:设 \(f(v)\) 表示 \(v\) 的倍数的出现次数,设 \(g(v)\) 表示 \(v\) 的出现次数,则
对每个数 \(v\) 再开个 std::bitset \(h[v]\),其中 \(h[v][v \cdot d] = \mu(d) \bmod 2\)。答案即为 \((a[x] \mathbin{\mathrm{and}} h[v]).\mathrm{count}() \bmod 2\)。
时间复杂度 \(\mathcal{O}(q(\sqrt{v} + \frac{v}{w}))\)。
OMRON Corporation Programming Contest 2025 (AtCoder Beginner Contest 397)
咕咕咕 ...
Codeforces Round 1010 (Div. 1, Unrated)
咕咕咕 ...
周天
CF 442C(*2500)
可以证明,若 \(a_i\) 两边的数均比 \(a_i\) 大,则最优策略肯定是先删掉 \(a_i\)。
将所有 V 形的 \(a_i\) 全都删去以后,会得到一个单峰序列。简单模拟可知,只有最大值与次大值无法取到,其他值均可取到。
CF 1407E(*2500)
考虑反过来考虑,设 \(\mathrm{dist}_u\) 表示在尽量阻碍行动的情况下 \(u\) 到 \(n\) 的最短路是多少。
考虑 bfs,每次扩展一个节点 \(u\) 时,考虑 \(u\) 经过颜色为 \(c\) 的反边到达的节点 \(v\):
- 若 \(v\) 还没被染色,则将点 \(v\) 染色成不是 \(c\) 的另外一个颜色。
- 若 \(v\) 已经被染色且颜色与 \(c\) 一致,则使用 \(\mathrm{dist}_u + 1\) 更新 \(\mathrm{dist}_v\),将 \(v\) 加入队列。
CF 1562E(*2500)
注意到 \(s[i, j + 1]\) 的字典序一定大于 \(s[i, j]\),故 \(s[i, j]\) 后面一定可以接上 \(s[i, j + 1]\)。
结论:一定存在一个最优解,满足若 \(s[i, j]\) 被选,则 \(s[i, j + 1 \sim n]\) 也被选。
考虑 dp,设 \(f(i)\) 表示最后一个选择 \(s[i, n]\) 时的最长上升子序列长度。
枚举上一次选择的 \(s[j, n]\),找到后缀 \(i\) 的第一个字典序大于 \(s[j, n]\) 的前缀,显然是 \(s[i, i + \mathrm{lcp}(j, i)]\)(其中必须满足 \(s_{i + \mathrm{lcp}(j, i)} > s_{j + \mathrm{lcp}(j, i)}\),否则就不存在字典序大于 \(s[j, n]\) 的前缀),此时有
时间复杂度 \(\mathcal{O}(n^2)\)。
CF 1111E(*2500)
考虑计数。设 \(c_1, c_2, \cdots, c_k\) 分别表示 \(a_1, a_2, \cdots, a_k\) 到根节点 \(r\) 的路径上有多少个关键点。则将 \(k\) 个关键点分进至多 \(m\) 个有标号组的方案数为
但由于组与组之间不区分(无标号),设 \(g(m)\) 表示将 \(k\) 个关键点分进恰好 \(m\) 个有标号组的方案数,则答案应为 \(\sum_{i = 1}^n \frac{g(i)}{i!}\)。
注意到(二项式反演)
故先求出 \(f(i)\),再求出 \(g(i)\),最后计算 \(\sum_{i = 1}^n \frac{g(i)}{i!}\) 即可。
至于 \(c_i\) 的处理,可以在 dfs 序上使用树状数组维护,并使用换根 Trick。
时间复杂度 \(\mathcal{O}(\sum k \log n + \sum km)\)。
CF 1096E(*2500)
复杂做法:枚举最大值 \(\mathrm{mx}\),枚举最大值个数 \(c\),计算剩余选手得分 \(< \mathrm{mx}\) 且和为 \(s - \mathrm{mx} \cdot c\) 的方案数。
不妨去掉小明得分 \(\geq r\) 的限制,此时每个人成为冠军的概率均等,均为 \(\frac{1}{n}\)。
" 小明得分 \(\geq r\) 且小明是冠军 " 等价于 " 冠军得分 \(\geq r\) 且小明是冠军 ",故我们只需计算冠军得分 \(\geq r\) 的概率,最后乘以 \(\frac{1}{n}\) 即可。
考虑容斥,钦定 \(i\) 个选手得分 \(\geq r\),先将这 \(i\) 个选手的得分减去 \(r\),故我们需要计算选手得分总和为 \(s - i \cdot r\) 的方案数,运用插板法可得
CF 696D(*2500)
评分虚高 ...
考虑建出 AC 自动机,当串匹配到 AC 自动机上的节点 \(p\) 时,该后缀产生的贡献,即为 fail 树上节点 \(p\) 到根节点路径上终止节点的价值总和。
于是预处理出匹配到 AC 自动机上的节点 \(p\) 产生的价值 \(\mathrm{value}(p)\),设 \(f(l, i)\) 表示构造了一个长度为 \(l\) 的字符串,匹配到 AC 自动机上的节点 \(p\) 时产生的最大价值,若节点 \(i\) 经过字符 \(c\) 到达节点 \(j\),则有转移
使用矩阵快速幂加速即可。
时间复杂度 \(\mathcal{O}((\sum |S_i|)^3 \log l)\)。
第四周(2025.03.17 ~ 2025.03.23)
周一
CF 1572B(*2500)
首先注意到,经过一次操作之后,所有数的异或和肯定不变。故有一个必要条件是,所有数的异或和为 \(0\)。
当 \(n\) 为奇数时,有一个构造:
- 先选择 \(n - 2, n - 4, \cdots, 3, 1\) 进行操作,此时 \(a_1 = 0\)(即所有数的异或和),且 \(a_{2i} = a_{2i + 1}\)。
- 再选择 \(1, 3, \cdots, n - 4, n - 2\) 进行操作,此时每次操作的位置 \(x\) 必定满足 \(a_x = 0, a_{x + 1} = a_{x + 2}\),故该次操作会使得 \(a_x = a_{x + 1} = a_{x + 2} = 0\)。
当 \(n\) 为偶数时,考虑找一个长度为奇数,异或和为 \(0\) 的前缀,然后对前后缀进行同 \(n\) 为奇数情况的构造。
可以证明,若找不到这样的前缀,则一定无解。因为此时原串形如 1aabb..zz1(即首尾均为 \(1\) 且 \(a_{2i} = a_{2i + 1}\)),不论如何操作仍然有 \(a_{2i} = a_{2i+1}\),首尾的 \(1\) 无法消掉。
CF 1637F(*2500)
注意到,叶子节点处是一定要建造塔的,否则该叶子一定无法被覆盖到。
其次,非叶子节点处是不必建塔的(因为不如把非叶子节点的塔挪到叶子节点)。
考虑以 \(h\) 值最大的节点为根 \(\mathrm{rt}\),则根节点必须要有两个不同的子树均包含 \(\geq h_{\mathrm{rt}}\) 的塔,其他点 \(u\) 则只需要保证子树内包含 \(\geq h_u\) 的塔即可(因为 \(u\) 的子树外一定有一个 \(\geq \max h\) 的塔)。
从下往上贪心,每次贪心地考虑子树 \(u\) 内已放置的塔的最大值 \(\mathrm{mx}\),若 \(\mathrm{mx} \geq h_u\) 就不用管;否则将 \(\mathrm{mx}\) 替换为 \(h_u\) 即可。特别地,根节点需要考虑子树内已放置的塔的最大值与次大值(需要来自两个不同的子树)。
CF 2077D(*3100)
考虑当子序列最大值 \(\mathrm{mx}\) 已经确定时,要如何求出字典序最大的子序列 \(s\)?
此时相当于要选出总和 \(> 2 \cdot \mathrm{mx}\) 的字典序最大的子序列。
考虑以下贪心过程:从左往右扫描每一个 \(a_i\),设 \(\mathrm{sum}\) 表示当前 \(s\) 元素之和。
- 取出当前 \(s\) 的最后一个元素 \(x\),若 \(a_i > x\) 且 \(\mathrm{sum} - x + \sum_{j = i}^n a_i > 2 \cdot \mathrm{mx}\),则可以将 \(x\) 替换为 \(a_i\)。
重复该过程直到无法替换或 \(s\) 为空。 - 将 \(a_i\) 放入当前 \(s\) 的末尾。
可以证明,子序列 \(s\) 的最大值一定是 \(\{a_i\}\) 的前 \(\log_2 A\) 大其中之一(其中 \(A\) 为值域)。
考虑一个序列 \(v\),其中 \(v\) 的任何子序列都不可以作为多边形的边长。则升序排序过后一定满足 \(v_i \geq \sum_{j = 1}^{i - 1}v_j\),为了最大化 \(v\) 的长度,有 \(v_1 = 1\) 且 \(v_i = 2^{i - 2}\)(\(i \geq 2\))。
故满足任何子序列都不可以作为多边形边长的序列 \(v\),长度不超过 \(\log_2 A\)。
换言之,长度超过 \(\log_2 A\) 的序列 \(v\),必定有一个子序列可以作为多边形的边长。
假设答案的子序列 \(s\) 的最大值不是 \(\{a_i\}\) 的前 \(\log_2 A\) 大其中之一,则将前 \(\log_2 A\) 大构成的子序列 \(t\) 取出,由上述推导,\(t\) 必定有一个子序列 \(t'\) 可以作为多边形的边长。将 \(t'\) 插入子序列 \(s\) 中,显然满足条件的同时字典序更大。
时间复杂度 \(\mathcal{O}(n \log A)\)。
CF 1444C(*2500)
本题要求的是,在 \(k\) 组点中选出两组点,使得它们的导出子图是二分图的方案数。称端点属于同一个组的边为同组边,端点不属于同一个组的边为异组边。
首先先将所有的同组边连上,并做一次二分图染色,求出每个点 \(u\) 所属于的连通块编号 \(\mathrm{belong}_u\) 以及二分图染色的颜色 \(\mathrm{col}_u\)。
正难则反,考虑求出 " 两组点原本均是二分图,但在两组点之间连边过后不是二分图 " 的数量,这样的两组点有一个前提条件是两组点之间有边,故数量已经缩小到了 \(\mathcal{O}(m)\) 级别。
考虑将类型相同的异组边(端点属于的两个组相同)放在一起考虑。考虑建一张新图,对于一个异组边 \((x, y)\):
- 若 \(\mathrm{col}_x = \mathrm{col}_y\),则连边 \((\mathrm{belong}_x, \mathrm{belong}_y, 1)\),表示 \(x, y\) 所在的连通块的颜色相反。
- 若 \(\mathrm{col}_x \neq \mathrm{col}_y\),则连边 \((\mathrm{belong}_x, \mathrm{belong}_y, 0)\),表示 \(x, y\) 所在的连通块的颜色相同。
对新图再进行一遍类二分图染色即可,若染色出现矛盾则即为所求。
Educational Codeforces Round 176 (Rated for Div. 2)
咕咕咕 ...
周二
CF 2075E
显然只有四类情况。
1. 行有一种不同的元素,列有一种不同的元素
此时方案数为 \((A + 1) \cdot (B + 1)\)。
2. 行有两种不同的元素,列有一种不同的元素
此时方案数为 \((A + 1) \cdot A \cdot (B + 1) \cdot (2^{n - 1} - 1)\)。
3. 行有一种不同的元素,列有两种不同的元素。
此时方案数为 \((B + 1) \cdot B \cdot (A + 1) \cdot (2^{n - 1} - 1)\)。
4. 行有两种不同的元素,列有两种不同的元素。
设行两种不同的元素为 \(a, b\),列两种不同的元素为 \(c, d\)。则有 \(a \neq b, c \neq d\),\(a, b \leq A\),\(c, d \leq B\),且 \(a \oplus c = b \oplus d\),移项得 \(a \oplus c \oplus b \oplus d = 0\)。
考虑数位 dp,设 \(f(k, 0/1, 0/1, 0/1, 0/1)\) 表示从高到低考虑到了第 \(k\) 位,\(a, b, c, d\) 的数位选取是否解除了限制(即不论怎么放均小于上界)。枚举每一位的选取情况进行转移即可。
要注意对 \(a = b, c = d\) 的情况进行去重,最后乘以 \((2^{n - 1} - 1) \cdot (2^{m - 1} - 1)\) 即可。
int n, m, A, B;
int f[30][2][2][2][2];
int dp(int k, int sa, int sb, int sc, int sd) {
if (k == -1) return 1;
if (~f[k][sa][sb][sc][sd]) return f[k][sa][sb][sc][sd];
int ma = sa ? A >> k & 1 : 1,
mb = sb ? A >> k & 1 : 1,
mc = sc ? B >> k & 1 : 1,
md = sd ? B >> k & 1 : 1;
int ans = 0;
for (int a = 0; a <= ma; a ++)
for (int b = 0; b <= mb; b ++)
for (int c = 0; c <= mc; c ++)
for (int d = 0; d <= md; d ++) {
if (a ^ b ^ c ^ d) continue;
add(ans, dp(k - 1, sa && a == ma, sb && b == mb, sc && c == mc, sd && d == md));
}
return f[k][sa][sb][sc][sd] = ans;
}
CF 2081B(*2500)
称满足 \(a_i > a_{i + 1}\) 的位置为不合法,则一次操作最多可以修改两个不合法的位置(操作 \(a_l, \cdots, a_r\),至多只能逆转 \(a_{l - 1} > a_l\) 与 \(a_r > a_{r + 1}\))。
设 \(s\) 为序列 \(a\) 中不合法位置的个数,则 \(l = \left\lceil \frac{s}{2} \right\rceil\) 显然是一个操作次数的下界。分两类情况来考虑。
1. \(s\) 为奇数
每次将头尾的两个不合法位置消去(将第二个单增段接到第一个单增段后面,将倒二个单增段接到倒一个单增段前面),到最后只剩下两个单增段(一个不合法的位置)。
故此时答案为 \(l\)。
2. \(s\) 为偶数
同奇数情况讨论,但会发现到最后只剩下一个单增段,但该单增段可能不能与两端相接(无法做到大于左边且小于右边)。
为了使得与两端相接,我们最好在重排单增段时,将单增段排成一个公差为 \(+1\) 的等差数列。设最左边与最右边的不合法对分别为 \((a_l, a_{l + 1}), (a_{r - 1}, a_r)\)。有一个必要条件是 \(a_r - a_l \geq r - l\),不难证明该条件也是充分的。
故当 \(a_r - a_l \geq r - l\) 时,答案为 \(l\);否则我们需要再花费一步的代价,答案为 \(l + 1\)。
周三
CF 1146F(*2500)
定义连接两个同组节点的边为染色边。若点 \(u\) 为最小连通子图的 LCA,则 \(u\) 必须向儿子连接 \(\geq 2\) 条染色边(否则 \(u\) 为叶子)。
考虑 dp,设 \(f(u, 0 / 1 / 2)\) 表示 \(u\) 向儿子连了 \(0 / 1 / \geq 2\) 条染色边时的方案数。对于 \(u\) 的每个儿子 \(v\),有转移
特别要注意的是,若 \(u\) 为叶子节点,则应该令 \(f(u, 2) = 1\)(因为此时 \(u\) 是被染色完毕的)。
时间复杂度 \(\mathcal{O}(n)\)。
CF 1687C(*2500)
首先,设 \(d_i = b_i - a_i\),则一个区间 \([l, r]\) 能操作当且仅当 \(\sum_{i = l}^r d_i = 0\),并将 \(d_l, \cdots, d_r\) 都赋值成 \(0\)。
进一步,设 \(s_i = \sum_{j = 1}^i d_j\),则一个区间 \([l, r]\) 能操作当且仅当 \(s_{l - 1} = s_r\),并将 \(s_l, \cdots, s_r\) 都赋值成 \(s_{l - 1}\)。目标是将 \(s_0, \cdots, s_n\) 全部清零。
可以注意到,当 \(s_{l - 1} = s_r \neq 0\) 时,操作一定是不优的。我们只进行满足 \(s_{l - 1} = s_r = 0\) 的操作。
故我们每次找一个满足 \(s_{l - 1} = s_r = 0\) 的操作,将 \(s_l, \cdots, s_r\) 全都赋值成 \(0\),直到无法操作为止。
考虑加速上述过程, 使用线段树维护一个区间是否存在非 \(0\) 数,每次区间赋值成 \(0\) 时,将该区间内的所有非 \(0\) 数改成 \(0\),并考虑其是否可以扩展出新区间。
时间复杂度 \(\mathcal{O}(m + n \log n)\)。
CF 1710C(*2500)
设 \(x = a \oplus b, y = b \oplus c, z = a \oplus c\),则 \(x \oplus y \oplus z = 0\)。
当且仅当 \(x, y, z\) 存在其中两个数的 \(\mathrm{and}\) 为 \(0\),三个数不能构成三角形三边长。
于是数位 dp 即可,设 \(f(k, 0/1, 0/1, 0/1, 0/1, 0/1, 0/1)\) 表示从高到低考虑到了第 \(k\) 位,\(a, b, c\) 的数位选取是否解除了限制,\((x, y), (y, z), (x, z)\) 是否有一位上均为 \(1\)。
CF 1481E(*2500)
显然,每本书至多被操作一次。注意到,被移动的书在序列后面可以任意排列。发现所有被拿出来的书中,最多有一种颜色的书没有被全部拿出来,且没有被全部拿出来的书应该排在序列最后。
正难则反,考虑计算最多有多少本书不用被操作。记完全留下来的颜色为 A 类,完全被移动的颜色为 B 类,排在最后未被完全拿出来的颜色为 C 类。
显然 A 类颜色对应的一定是一段区间,并且区间中的其他颜色一定都要被拿出来。相当于把整个序列划分为若干段 A 类颜色对应的区间(可以不相接,但不能有交),A 类颜色中的其他颜色都必须被选为 B 类颜色,除了最后的颜色可以不拿出来而作为 C 颜色。
设 \(f(i)\) 表示 \(i\) 到 \(n\) 最多有多少本书不用被操作,有三种转移:
- \(i\) 为 A 类,则此时 \(i\) 一定是颜色 \(a_i\) 的最靠左的位置(即 \(Lp(a_i) = i\)),此时有
- \(i\) 为 B 类,此时有
- \(i\) 为 C 类,此时有
CF 547D(*2600)
考虑将 \(x\) 坐标相同的点,两个点一组进行配对连边(剩一个则不用管),考虑将 \(y\) 坐标相同的点,两个点一组进行配对连边(剩一个则不用管)。
连边形成的图显然为二分图,对图进行二分图染色即可。
CF 321E(*2600)
显然可以写一个很暴力的 dp。设 \(f(i, j)\) 表示考虑到了前 \(i\) 项,划分了 \(j\) 段时的最小代价,则有
其中 \(\mathrm{cost}(l, r) = \sum\limits_{i = l}^{r - 1}\sum\limits_{j = i + 1}^r u_{i, j}\),可以使用二位前缀和预处理。
盲猜该 dp 具有决策单调性。使用 "决策单调性优化 dp:分治" 优化至 \(\mathcal{O}(kn \log n)\)。
周四
CF 1830D(*2800)
考虑以同色连通块的视角处理此题。
注意到横跨至少一个全 \(0\) 连通块与全 \(1\) 连通块的路径 \(\mathrm{mex} = 2\),在全 \(0\) 连通块内的路径 \(\mathrm{mex} = 1\),全 \(1\) 连通块内的路径 \(\mathrm{mex} = 0\)。
于是我们反过来考虑。设一开始所有路径均有 \(2\) 的贡献,对于一个大小为 \(k\) 的全 \(0\) 连通块有 \(\frac{k(k + 1)}{2}\) 的负贡献,对于一个大小为 \(k\) 的全 \(1\) 连通块有 \(k(k + 1)\) 的负贡献。
一个不成熟的想法是对这棵树进行黑白染色,黑白染色的负贡献 \(\leq 2n\)。但有时黑白染色并不是最优的,例如将两个菊花图的中心以一条边相连,最优的做法是将两个中心染成 \(1\),将叶子染成 \(0\)。
但可以通过黑白染色可以进一步约束连通块的大小 \(k\),有 \(\frac{k(k + 1)}{2} \leq 2n \implies k \leq \sqrt{4n}\)。
故直接考虑 dp,设 \(f(u, i, 0 / 1)\) 表示考虑到了以 \(u\) 为根的子树,\(u\) 所在的连通块大小为 \(i\) 颜色为 \(0/1\) 时的最小负贡献。转移很简单 ...
时间复杂度 \(\mathcal{O}(n\sqrt{n})\),但此题还卡了空间复杂度 \(\mathcal{O}(n\sqrt{n})\) 的实现。
官方给出的解决方案是 [Idea] Using HLD to reduce memory。
18Michael 大佬给出的解决方案是,使用 std::vector 来储存 dp 数组,每次枚举 \(u\) 的子节点 \(v\) 转移之后,将 \(v\) 的 dp 数组进行 clear() 以及 shrink_to_fit()。可以证明空间复杂度是 \(\mathcal{O}(n)\) 的(容量不超过 \(k\) 不重要,容量不超过子树大小比较重要)。
2021-2022 Russia Team Open, High School Programming Contest (VKOSHP XXII)
咕咕咕 ...
周五
CF 1146C(*1700)
要通过询问两个点集 \(A, B\) 之间最大距离的方式,得到任意两个点之间的最大距离。
显然可以二进制分组,对于一个二进制位 \(i\),若一个点在二进制下第 \(i\) 位为 \(1\) 则将其分入 \(A\) 集合;否则将其分入 \(B\) 集合。任意两个不同的点必定会在一次分组中被分进两个不同的集合。
周六
CF 1223F(*2600)
可以考虑模拟出每一个前缀的栈情况 \(s_i\),若区间 \([l, r]\) 可以被消除,则前缀 \(l - 1\) 与前缀 \(r\) 的栈状态必定相同(即 \(s_{l - 1} = s_{r}\)),于是计算出每个前缀的栈情况哈希值进行计数即可。
CF 436E(*2600)
考虑贪心,每次都选择代价较小的方式增加一颗星。若只考虑零星变一星,一星变两星,则显然会出现后效性。故我们考虑反悔贪心
- 选择一个零星变一星。
- 选择一个一星变两星。
- 选择一个两星变一星,选择一个零星变两星。
- 选择一个一星变零星,选择一个零星变两星。
故我们开五个堆维护贪心过程即可。
int type[N];
template <const int Type, const int HeapType> /* HeapType 为 +1/-1 表示这个堆是 大根堆/小根堆 */
struct heap {
std::priority_queue< std::pair<int, int> > q;
std::pair<int, int> query() {
while (q.size() && type[q.top().second] != Type) q.pop();
std::pair<int, int> ans = q.size() ? q.top() : std::make_pair(-inf, 0);
ans.first *= HeapType;
return ans;
}
void insert(int x, int pos) {
std::pair<int, int> dat = {x, pos};
dat.first *= HeapType;
q.push(dat);
}
};
/*
堆一:0 的最小 a_i
堆二:0 的最小 b_i
堆三:1 的最小 b_i - a_i
堆四:1 的最大 a_i
堆五:2 的最大 b_i - a_i
*/
heap<0, -1> q1;
heap<0, -1> q2;
heap<1, -1> q3;
heap<1, +1> q4;
heap<2, +1> q5;
CF 3D(*2600)
将左括号 ( 看成 \(+1\),将右括号 ) 看成 \(-1\),则一个括号串合法的条件是:
- 每个前缀均 \(\geq 0\)。
- 总和 \(=0\)。
考虑贪心,一开始将所有的 ? 全替换为 \()\),每次遇到一个前缀 \(<0\) 时,就将前面替换代价最小的 ? 从 ) 替换为 (。
UNIQUE VISION Programming Contest 2025 Spring (AtCoder Beginner Contest 398)
咕咕咕 ...
Codeforces Round 1011 (Div. 2)
咕咕咕 ...
周天
CF 741C(*2600)
考虑将所有的 \(2i - 1, 2i\) 进行连边(1 类边),将所有的情侣 \(a_i, b_i\) 进行连边(2 类边)。可以证明得到的图是一张二分图,对该图进行二分图染色即可。
记 \(2i - 1, 2i\) 为第 \(i\) 组节点,因为一条路径必然是 1 类边 2 类边 1 类边 2 类边 ... 交替进行的,想要到达不同组必须经过 2 类边,故不会出现奇环。
Codeforces Round 1012 (Div. 1)
咕咕咕 ...
AtCoder Regular Contest 195 (Div. 2)
咕咕咕 ...
第五周(2025.03.24 ~ 2025.03.30)
周一
CF 917D(*2600)
考虑钦定原树中的一些边已经被选进生成树时,生成树个数要怎么计算。注意到钦定的边会将原图缩成若干个连通块,连通块的大小分别为 \(a_1, a_2, \cdots, a_k\),考虑一条连接连通块 \(x, y\) 的边,方案数显然是 \(a_x \cdot a_y\),设 \(d_i\) 表示连通块 \(i\) 在生成树中的度数,则方案数为 \(\prod_{i=1}^n a_i^{d_i}\)。由 prufer 序列可知,总方案数为
考虑钦定原树中的 \(i\) 条边(则会产生 \(n - i\) 个连通块)已经被选进生成树时的方案数为 \(\mathrm{cnt}(i)\),恰好原树的 \(i\) 条边被选进生成树的方案数为 \(g(i)\)。则有
于是可以考虑先求出 \(\mathrm{cnt}\) 再反演出 \(g\)。
注意到 \(\prod_{i = 1}^k a_i\) 不太好直接处理。Trick:每个部分大小的乘积等于每个部分各选出一个元素的方案数。
考虑 dp,设 \(f(u, i, 0/1)\) 表示考虑到了 \(u\) 的子树,已经选出了 \(i\) 个连通块,且 \(u\) 所在的连通块 暂未 / 已经 选出一个点的方案数。枚举 \(u\) 的每一个儿子 \(v\),有转移
- 不合并连通块。
- 合并连通块。
于是 \(\mathrm{cnt}(i) = f(1, n - i, 1) \cdot n^{n - i - 2}\)。
时间复杂度 \(\mathcal{O}(n^2)\)。
周二
gym103483 J
将切割后的网格边界线标记出来,可以得到两条折线。
上方的折线 \((1, 2) \to (n, m + 1)\),下方的折线 \((2, 1) \to (n + 1, m)\),且不能有交点。
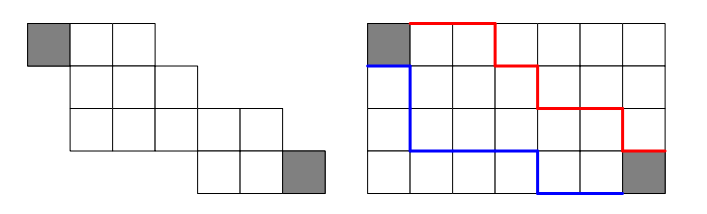
理解方式 1:LGV 引理。设起点 \(s_1 = (1, 2), s_2 = (2, 1)\),终点 \(e_1 = (n, m + 1), e_2 = (n + 1, m)\),设 \(\mathrm{calc}(s, e)\) 表示从点 \(s\) 到点 \(e\) 的方案数。
则不交路径数为
理解方式 2:折线容斥。若不考虑折线不能有交点,则答案为 \(\mathrm{calc}(s_1, e_1) \cdot \mathrm{calc}(s_2, e_2)\)。
现在我们要从答案中减去相交对的数量,考虑两条折线的最后一个交点,我们将这两条路径的终点交换。
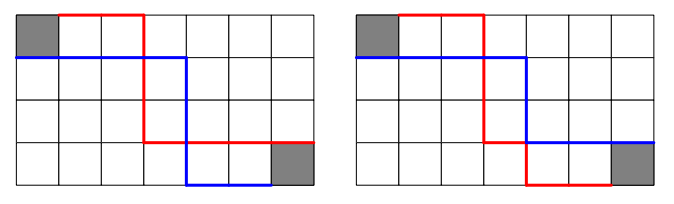
故相交的折线个数即为 \((1, 2) \to (n + 1, m)\) 与 \((2, 1) \to (n, m + 1)\) 的折线个数之积。故答案为
gym103483 H
设 \(\mathrm{up}(x)\) 表示开口向下的二次函数在横坐标 \(x\) 处的最小纵坐标 \(y\),\(\mathrm{dn}(x)\) 表示开口向上的二次函数在横坐标 \(x\) 处的最大纵坐标 \(y\)。
不难发现 \(\mathrm{up}(x)\) 是单峰的,\(\mathrm{dn}(x)\) 是单谷的。故 \(\mathrm{up}(x) - \mathrm{dn}(x)\) 是单峰的,由题意我们只需找一个 \(\mathrm{up}(x) - \mathrm{dn}(x) > 0\) 的点 \(x\) 即可,于是三分查找 \(\mathrm{up}(x) - \mathrm{dn}(x)\) 的峰值。
gym103483 C
考虑建出 Trie 树,设 \(\mathrm{cnt}[u]\) 表示节点 \(u\) 上的终止节点个数,设 \(\mathrm{sze}[u]\) 表示节点 \(u\) 的子树内的终止节点个数。
设 \(\mathrm{go}(u, c)\) 表示节点 \(u\) 往节点 \(\delta(u, c)\) 走产生的贡献,则 \(\mathrm{go}(u, c) = \mathrm{cnt}[u] + \sum_{i < c} \mathrm{sze}[\delta(u, i)]\)。
考虑把贡献记在点上,即 \(\mathrm{value}(\delta(u, c)) = \mathrm{go}(u, c)\),则一个字符串 \(s\) 对应的答案即为其在 Trie 树上经过的节点的贡献之和(叶子需要特殊考虑)。
于是我们只需维护字符串 \(s\) 在 Trie 树上的位置即可。维护 \(\mathrm{end}(u, c)\) 表示节点 \(u\) 一直沿着字符 \(c\) 走到达的节点。使用树上倍增向上走,\(\mathrm{end}\) 数组向下走。特别处理一下叶子节点的贡献(即字符串 \(s\) 走出了 Trie 树)即可。
MENASQ_TGRM 大佬的优秀做法:在 \(\mathrm{end}(u, c)\) 中约束向下走到达的节点深度,深度 \(\leq n\) 即可。
Codeforces Round 1013 (Div. 3)
咕咕咕 ...
周三
CF 1208F(*2600)
CF 1446D1(*2600)
CF 1446D2(*3000)
CF 241E(*2600)
CF 10E(*2600)
周四
The 2021 ICPC Southeastern Europe Regional Contest
咕咕咕 ...
周五
CF 1207E(*1900)
周六
Codeforces Round 1014 (Div. 2)
咕咕咕 ...


 浙公网安备 33010602011771号
浙公网安备 33010602011771号