The 2025 Hunan Collegiate Programming Contest
Preface
不知道 VP 什么就找了场 QOJ 上最新的比赛,结果发现打的时候就我们一个队,全程无榜就很难受
而且这场的题目质量确实让人不敢恭维,一堆原题和典题,基本没有那种有意思的思维题
最后 9 of 11,剩下两个感觉都是细节分讨,属于会了一点又没完全会,一点不想写了
A. 定制最短路
套路题,把一条路径看作(路径上边数,路径长度)的二元组
前者显然是斜率,后者是截距,简单求个半平面交即可
#include<bits/stdc++.h>
using namespace std;
#define int long long
using pii = pair<int, int>;
const int N = 5005;
const int INF = (int)1e18+5;
const int MOD = 998244353;
void inc(int &x, int a) { if ((x+=a)>=MOD) x-=MOD;}
int n, m;
int dis[2][N], cnt[2][N], ndis[N], ncnt[N];
vector<pii> G[N];
array<int, 2> stk[N]; int tp=-1;
void solve() {
cin >> n >> m;
for (int i=1; i<=n; ++i) G[i].clear();
for (int i=1; i<=m; ++i) {
int u, v, w; cin >> u >> v >> w;
G[u].push_back({v, w}); G[v].push_back({u, w});
}
tp = -1;
ndis[0] = INF;
for (int i=1; i<=m; ++i) ndis[i]=0, ncnt[i]=0;
for (int x=1; x<=n; ++x) dis[0][x] = INF, cnt[0][x] = 0;
dis[0][1] = 0, cnt[0][1] = 1;
for (int i=1; i<=m; ++i) {
for (int x=1; x<=n; ++x) dis[i%2][x] = INF, cnt[i%2][x] = 0;
for (int x=1; x<=n; ++x) {
for (auto [v, w] : G[x]) {
if (dis[i%2][v] > dis[(i-1)%2][x]+w) {
dis[i%2][v] = dis[(i-1)%2][x]+w;
cnt[i%2][v] = cnt[(i-1)%2][x];
} else if (dis[i%2][v] == dis[(i-1)%2][x]+w) {
inc(cnt[i%2][v], cnt[(i-1)%2][x]);
}
}
// printf("i=%lld x=%lld dis: ", i, x); for (int j=1; j<=n; ++j) printf("%lld ", dis[i%2][j]); puts("");
// printf("i=%lld x=%lld cnt: ", i, x); for (int j=1; j<=n; ++j) printf("%lld ", cnt[i%2][j]); puts("");
}
if (dis[i%2][n] < INF) ndis[i] = dis[i%2][n], ncnt[i] = cnt[i%2][n];
}
// printf("ndis: "); for (int i=1; i<=m; ++i) printf("%lld ", ndis[i]); puts("");
// printf("ncnt: "); for (int i=1; i<=m; ++i) printf("%lld ", ncnt[i]); puts("");
for (int i=1; i<=m; ++i) {
if (ndis[i] == 0) continue;
if (tp>=0 && ndis[i]>ndis[stk[tp][0]]) continue;
// printf("i=%lld\n", i);
int x = INF;
while (tp>=0 && (x=(ndis[stk[tp][0]]-ndis[i])/(i-stk[tp][0]))>stk[tp][1]) --tp;
if (tp>=0) x=(ndis[stk[tp][0]]-ndis[i])/(i-stk[tp][0]);
++tp; stk[tp][0] = i; stk[tp][1] = x;
}
// printf("stk:"); for (int i=0; i<=tp; ++i) printf("(%lld %lld)", stk[i][0], stk[i][1]); puts("");
int ans = 0;
for (int i=0; i<=tp; ++i) inc(ans, ncnt[stk[i][0]]);
cout << ans << '\n';
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0);
int T; cin >> T; while (T--) solve();
return 0;
}
B. Cut ellipse
将椭圆伸缩变为圆后转化为计算圆版本的面积即可
注意原点在哪一侧哪边面积就更大
#include <bits/stdc++.h>
using real = long double;
int main() {
int a, b, k, c;
std::cin >> a >> b >> k >> c;
std::cout << std::fixed << std::setprecision(15);
real d = std::abs(real(c)) / std::sqrt(real(a * a) * real(k * k) + real(b * b));
if(d >= 1.0) {
std::cout << real(0) << char(10);
return 0;
}
real theta = real(2.0) * std::acos(d / real(1.0));
real ars = real(0.5) * theta;
real ans = std::numbers::pi - ars + d * std::sqrt(1.0 - d * d);
std::cout << ans * a * b << char(10);
return 0;
}
D. Box
总感觉这题最近做过
注意到 \(3\times 3\) 的情形有答案为 \(2\) 的构造法,因此对于 \(n=m\ge 3\) 均有答案 \(n-1\) 的构造法
对于 \(\min(n,m)\le 2\) 以及 \(n\ne m\) 的情形,显然答案为 \(\min(n,m)\)
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
int t,n,m;
int main()
{
for (scanf("%d",&t);t;--t)
{
scanf("%d%d",&n,&m);
bool swaped=0;
if (n>m) swap(n,m),swaped=1;
if (n<=2)
{
printf("%d\n",n);
for (RI i=1;i<=n;++i)
if (swaped) printf("1 1 %d\n",i); else printf("1 %d 1\n",i);
continue;
}
if (n==m)
{
printf("%d\n",n-1);
printf("1 2 2\n");
printf("2 2 2\n");
for (RI i=4;i<=n;++i)
printf("1 %d %d\n",i,i);
continue;
}
printf("%d\n",n);
for (RI i=1;i<=n;++i)
if (swaped) printf("1 1 %d\n",i); else printf("1 %d 1\n",i);
}
return 0;
}
E. 矩阵构造
直接把所有数顺次填入即为一组合法解
证明的话考虑如果选的子矩形的边长均为偶数,则所有数的和也一定为偶数
否则从某个边权为奇数的那边考虑,从另一个方向对数求和后,得到一个项数为奇数的等差数列,则其和一定是中间项的倍数
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=55;
int n,m;
int main()
{
scanf("%d%d",&n,&m);
puts("Yes");
for (RI i=1;i<=n;++i)
for (RI j=1;j<=m;++j)
printf("%d%c",(i-1)*m+j," \n"[j==m]);
return 0;
}
F. Mod
把扩展欧拉定理的形式写出来,会发现我们要对每个数 \(a_i\) 维护
以及 \(a_i\) 的实际值关于 \(m,\phi(m),\phi(\phi(m)),\dots\) 的大小关系
简单实现即可,复杂度 \(O(n\log^2 m)\)
PS:有人比赛时实现把 \(x,y\) 当作 char 类型读入了,没有人类了
#include<cstdio>
#include<iostream>
#include<vector>
#define RI register int
#define CI const int&
#define fi first
#define se second
using namespace std;
typedef pair <int,int> pi;
const int N=210000;
int n,m; vector <pi> a[N]; vector <int> M;
inline int getphi(int x)
{
int res=x;
for (RI i=2;i*i<=x;++i)
if (x%i==0)
{
res-=res/i;
while (x%i==0) x/=i;
}
if (x>1) res-=res/x;
return res;
}
inline pi add(const pi& A,const pi& B,CI mod)
{
pi C={(A.fi+B.fi)%mod,A.se|B.se};
if (A.fi+B.fi>=mod) C.se=1;
return C;
}
inline pi mul(const pi& A,const pi& B,CI mod)
{
pi C={1LL*A.fi*B.fi%mod,A.se|B.se};
if (1LL*A.fi*B.fi>=1LL*mod) C.se=1;
return C;
}
inline pi quick_pow(pi A,int p,CI mod)
{
pi res={1,1>=mod};
for (;p;p>>=1,A=mul(A,A,mod)) if (p&1) res=mul(res,A,mod);
return res;
}
int main()
{
scanf("%d%d",&n,&m);
int x=m; M.push_back(x);
do
{
x=getphi(x);
M.push_back(x);
} while (x!=1);
// for (auto x:M) printf("%d ",x); putchar('\n');
for (RI i=1;i<=n;++i)
{
char opt[5]; int x,y;
scanf("%s%d",opt,&x);
if (opt[0]=='=')
{
for (auto mod:M)
a[i].push_back({x%mod,x>=mod});
} else if (opt[0]=='+')
{
scanf("%d",&y);
for (RI j=0;j<(int)M.size();++j)
{
int mod=M[j];
a[i].push_back(add(a[x][j],a[y][j],mod));
}
} else if (opt[0]=='*')
{
scanf("%d",&y);
for (RI j=0;j<(int)M.size();++j)
{
int mod=M[j];
a[i].push_back(mul(a[x][j],a[y][j],mod));
}
} else
{
scanf("%d",&y);
for (RI j=0;j+1<(int)M.size();++j)
{
int mod=M[j];
if (a[y][j+1].se)
{
a[i].push_back(quick_pow(a[x][j],a[y][j+1].fi+M[j+1],mod));
} else
{
a[i].push_back(quick_pow(a[x][j],a[y][j+1].fi,mod));
}
}
a[i].push_back({0,1});
}
printf("%d\n",a[i][0].fi);
}
return 0;
}
G. 禁止超速
考虑求出对于每个摄像头 \(i\),从起点到它全程卡着限速所需的总时间 \(pfx_i\),这个显然可以双指针快速求出
如果两个相邻摄像头 \(i,j\) 之间没有超速,则满足 \(pfx_j-pfx_i\le t_j-t_i\),即 \(t_i-pfx_i\le t_j-pfx_j\)
要删掉最少的摄像头,等价于保留最多的摄像头,因此对 \(\{t_i-pfx_i\}\) 求一个 LIS 即可
注意可以通过将坐标与时间都乘上所有可能的速度的 LCM,以避免小数除法带来的误差
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#define int long long
#define RI register int
#define CI const int&
using namespace std;
const int N=200005,INF=1e18;
int T,n,m,l,a[N],x[N],t[N],v[N],pfx[N];
class Tree_Array
{
private:
int mx[N],lim;
public:
#define lowbit(x) (x&-x)
inline void init(CI n)
{
lim=n; for (RI i=1;i<=lim;++i) mx[i]=-INF;
}
inline void add(RI x,CI y)
{
for (;x<=lim;x+=lowbit(x)) mx[x]=max(mx[x],y);
}
inline int get(RI x,int res=-INF)
{
for (;x;x-=lowbit(x)) res=max(res,mx[x]); return res;
}
#undef lowbit
}BIT;
signed main()
{
vector <int> speed={5, 10, 15, 20, 25, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120};
int S=1;
for (auto v:speed) S=S/__gcd(S,v)*v;
// return printf("%lld\n",S),0;
for (scanf("%lld",&T);T;--T)
{
scanf("%lld%lld%lld",&n,&m,&l);
scanf("%lld",&t[m+1]); t[m+1]*=S;
for (RI i=1;i<n;++i)
scanf("%lld",&a[i]),a[i]*=S;
for (RI i=1;i<=n;++i) scanf("%lld",&v[i]);
for (RI i=1;i<=m;++i)
scanf("%lld%lld",&x[i],&t[i]),x[i]*=S,t[i]*=S;
a[n]=x[m+1]=l*S; pfx[0]=0;
for (RI i=1,j=1;i<=m+1;++i)
{
int lst=x[i-1];
pfx[i]=pfx[i-1];
while (j<=n&&a[j]<=x[i])
{
pfx[i]+=(a[j]-lst)/v[j];
lst=a[j]; ++j;
}
if (j<=n) pfx[i]+=(x[i]-lst)/v[j];
lst=x[i];
}
// for (RI i=0;i<=m+1;++i) printf("%lld%c",t[i]-pfx[i]," \n"[i==m+1]);
vector <int> rst;
for (RI i=0;i<=m+1;++i)
rst.push_back(t[i]-pfx[i]);
sort(rst.begin(),rst.end());
rst.erase(unique(rst.begin(),rst.end()),rst.end());
for (RI i=0;i<=m+1;++i)
pfx[i]=lower_bound(rst.begin(),rst.end(),t[i]-pfx[i])-rst.begin()+1;
// for (RI i=0;i<=m+1;++i) printf("%lld%c",pfx[i]," \n"[i==m+1]);
BIT.init((int)rst.size());
BIT.add(pfx[0],1);
for (RI i=1;i<=m;++i)
BIT.add(pfx[i],BIT.get(pfx[i])+1);
int ans=BIT.get(pfx[m+1]);
if (ans<0) puts("-1"); else printf("%lld\n",m+1-ans);
}
return 0;
}
H. Prime Segments
究极无敌典题,求出前缀和数组,并将其转化为统计出现个数的形式
做差可以转化为反转其中一个数组,大力 FFT 卷积后把差值为质数的所有位置加起来即可
#include<cstdio>
#include<iostream>
#include<cmath>
#define RI register int
#define CI const int&
using namespace std;
const int N=1e6+5;
typedef long double LDB;
namespace Poly
{
const LDB PI=acosl(-1);
struct Complex
{
LDB x,y;
inline Complex(const LDB& X=0,const LDB& Y=0)
{
x=X; y=Y;
}
inline Complex conj(void)
{
return Complex(x,-y);
}
friend inline Complex operator + (const Complex& A,const Complex& B)
{
return Complex(A.x+B.x,A.y+B.y);
}
friend inline Complex operator - (const Complex& A,const Complex& B)
{
return Complex(A.x-B.x,A.y-B.y);
}
friend inline Complex operator * (const Complex& A,const Complex& B)
{
return Complex(A.x*B.x-A.y*B.y,A.x*B.y+A.y*B.x);
}
}; int lim,p,rev[N<<3];
inline void init(CI n)
{
for (lim=1,p=0;lim<=n;lim<<=1,++p);
for (RI i=0;i<lim;++i) rev[i]=(rev[i>>1]>>1)|((i&1)<<p-1);
}
inline void FFT(Complex *f,CI opt)
{
for (RI i=0;i<lim;++i) if (i<rev[i]) swap(f[i],f[rev[i]]);
for (RI i=1;i<lim;i<<=1)
{
Complex D(cosl(PI/i),opt*sinl(PI/i));
for (RI j=0;j<lim;j+=(i<<1))
{
Complex W(1,0);
for (RI k=0;k<i;++k,W=W*D)
{
Complex x=f[j+k],y=W*f[i+j+k];
f[j+k]=x+y; f[i+j+k]=x-y;
}
}
}
if (opt==-1)
{
for (RI i=0;i<lim;++i) f[i].x/=lim,f[i].y/=lim;
}
}
}
using namespace Poly;
int t,n,m,pfx[N]; Complex A[N<<3],B[N<<3];
int isprime[N],pri[N],cnt;
inline void sieve(CI n)
{
for (RI i=2;i<=n;++i)
{
if (!isprime[i]) pri[++cnt]=i;
for (RI j=1;j<=cnt&&i*pri[j]<=n;++j)
{
isprime[i*pri[j]]=1;
if (i%pri[j]==0) break;
}
}
}
int main()
{
for (scanf("%d",&t),sieve(1e6);t;--t)
{
scanf("%d",&n);
for (RI i=1;i<=n;++i)
{
int x; scanf("%d",&x);
pfx[i]=pfx[i-1]+x;
}
m=pfx[n];
for (RI i=1;i<=n;++i) A[pfx[i]].x+=1.0l;
for (RI i=0;i<n;++i) B[m-pfx[i]].x+=1.0l;
// for (RI i=0;i<=m;++i) printf("%d%c",(int)A[i].x," \n"[i==m]);
// for (RI i=0;i<=m;++i) printf("%d%c",(int)B[i].x," \n"[i==m]);
init(2*m); FFT(A,1); FFT(B,1);
for (RI i=0;i<lim;++i) A[i]=A[i]*B[i];
FFT(A,-1); long long ans=0;
// for (RI i=0;i<=2*m;++i) printf("%d%c",(int)A[i].x," \n"[i==2*m]);
for (RI i=2;i<=m;++i)
if (!isprime[i])
{
// printf("i = %d, val = %d\n",i,(int)(A[m+i].x+0.5l));
ans+=(long long)(A[m+i].x+0.5l);
}
printf("%lld\n",ans);
for (RI i=0;i<lim;++i) A[i]=B[i]=Complex();
}
return 0;
}
I. 撕纸
题目等价于坐标系上走路并不经过某个矩形内部的方案数
简单转化后发现一条合法的路径为恰好自下而上穿过以下蓝色线段的路径,计数是 trivial 的
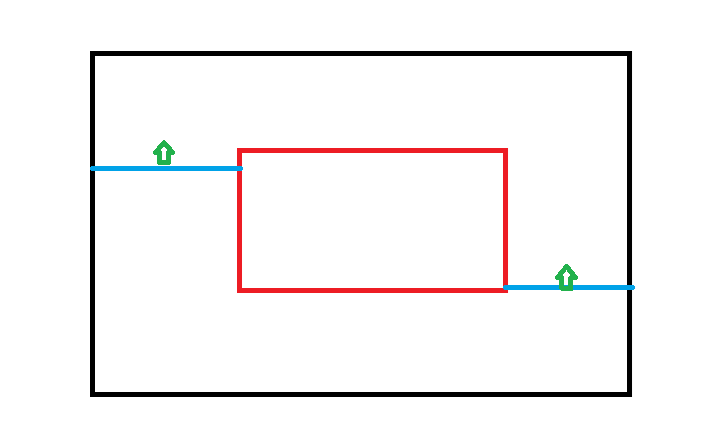
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
const int N=1e6+1e3+5,mod=998244353;
int t,n,m,a,b,c,d,fact[N],ifac[N];
inline int quick_pow(int x,int p=mod-2,int mul=1)
{
for (;p;p>>=1,x=1LL*x*x%mod) if (p&1) mul=1LL*mul*x%mod; return mul;
}
inline void init(CI n)
{
fact[0]=1;
for (RI i=1;i<=n;++i) fact[i]=1LL*fact[i-1]*i%mod;
ifac[n]=quick_pow(fact[n]);
for (RI i=n-1;i>=0;--i) ifac[i]=1LL*ifac[i+1]*(i+1)%mod;
}
inline int C(CI n,CI m)
{
if (n<0||m<0||n<m) return 0;
return 1LL*fact[n]*ifac[m]%mod*ifac[n-m]%mod;
}
inline int F(CI a,CI b,CI c,CI d) // ways of (a,b) -> (c,d)
{
if (a>c||b>d) return 0;
return C(c-a+d-b,c-a);
}
int main()
{
for (scanf("%d",&t),init(1e6+1e3);t;--t)
{
scanf("%d%d%d%d%d%d",&n,&m,&a,&b,&c,&d);
int ans=0;
for (RI x=0;x<=a;++x)
{
// printf("(%d %d)\n",x,d-1);
// printf("%d %d\n",F(0,0,x,d-1),F(x,d,n,m));
(ans+=1LL*F(0,0,x,d-1)*F(x,d,n,m)%mod)%=mod;
}
for (RI x=c;x<=n;++x)
{
// printf("(%d %d)\n",x,b);
// printf("%d %d\n",F(0,0,x,b),F(x,b+1,n,m));
(ans+=1LL*F(0,0,x,b)*F(x,b+1,n,m)%mod)%=mod;
}
// printf("a / b = %d / %d\n",ans,F(0,0,n,m));
printf("%d\n",1LL*ans*quick_pow(F(0,0,n,m))%mod);
}
return 0;
}
K. Character Walk
直接 DP 复杂度是 \(O(n^2)\) 的,但可以用回文树的性质,固定一个端点后回文串长是 \(O(\log n)\) 个等差序列
#include <algorithm>
#include <cstring>
#include <iostream>
#include <string>
#include <vector>
using namespace std;
using ll = long long;
constexpr int MAXN = 1000000 + 5;
namespace pam {
int sz, tot, last;
int ch[MAXN][26], len[MAXN], fail[MAXN];
int cnt[MAXN], dep[MAXN], dif[MAXN], slink[MAXN];
char s[MAXN];
int node(int l) { // 建立一个长度为 l 的新节点
sz++;
memset(ch[sz], 0, sizeof(ch[sz]));
len[sz] = l;
fail[sz] = 0;
cnt[sz] = 0;
dep[sz] = 0;
return sz;
}
void clear() { // 初始化
sz = -1;
last = 0;
s[tot = 0] = '$';
node(0);
node(-1);
fail[0] = 1;
}
int getfail(int x) { // 找到后缀回文
while (s[tot - len[x] - 1] != s[tot]) x = fail[x];
return x;
}
void insert(char c) { // 建树
s[++tot] = c;
int now = getfail(last);
if (!ch[now][c - 'a']) {
int x = node(len[now] + 2);
fail[x] = ch[getfail(fail[now])][c - 'a'];
dep[x] = dep[fail[x]] + 1;
ch[now][c - 'a'] = x;
dif[x] = len[x] - len[fail[x]];
if (dif[x] == dif[fail[x]])
slink[x] = slink[fail[x]];
else
slink[x] = fail[x];
}
last = ch[now][c - 'a'];
cnt[last]++;
}
} // namespace pam
using pam::dif;
using pam::fail;
using pam::len;
using pam::slink;
int n, dp[MAXN], g[MAXN];
string s;
char t[MAXN];
vector<int> work() {
pam::clear();
memset(dp, 0x3f, sizeof(int) * (n + 1));
dp[0] = 0;
for (int i = 1; i <= n; i++) {
pam::insert(s[i]);
for (int x = pam::last; x > 1; x = slink[x]) {
g[x] = dp[i - len[slink[x]] - dif[x]];
if (dif[x] == dif[fail[x]]) g[x] = min(g[x], g[fail[x]]);
dp[i] = min(dp[i], g[x] + 1);
}
}
return vector(dp, dp + n + 1);
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
cin >> s;
n = s.size();
s = string(" ") + s;
auto dp1 = work();
reverse(s.begin() + 1, s.end());
auto dp2 = work();
// for(int i = 0; i <= n; ++i) cerr << dp1[i] << char(i == n ? 10 : 32);
// for(int i = 0; i <= n; ++i) cerr << dp2[i] << char(i == n ? 10 : 32);
int q; cin >> q;
for(int i = 0, a; i < q; ++i) {
cin >> a;
cout << min(dp1[a], dp2[n - a]) << char(i == q - 1 ? 10 : 32);
}
return 0;
}
Postscript
下次 VP 找场次前还是先找个打到人多且口碑好点的场吧


 浙公网安备 33010602011771号
浙公网安备 33010602011771号