The 3rd Universal Cup. Stage 35: Kraków
Preface
开学后反而比暑假空了好多,平时都可以抽时间 VP 了
这场只能说许久未训糖的没边,基本上没一个题写的顺的
最后时间不够 H 也不知道错哪了,连 8 题的基本线都没达到
C. Diamonds and the Genie
直接把是否左转过以及上一步走的方向放到状态里 BFS 即可
之所以要加上方向是为了防止重复走到某个点导致贡献计算重复
#include<cstdio>
#include<iostream>
#include<queue>
#include<array>
#define int long long
#define RI register int
#define CI const int&
using namespace std;
const int N=3005;
int t,n,m,A[N][N],f[N][N][2][3];
signed main()
{
for (scanf("%lld",&t);t;--t)
{
scanf("%lld%lld",&n,&m);
for (RI i=1;i<=n;++i)
for (RI j=1;j<=m;++j)
{
scanf("%lld",&A[i][j]);
for (RI a=0;a<2;++a)
for (RI b=0;b<3;++b)
f[i][j][a][b]=-1e18;
}
queue <array <int,4>> q;
f[1][1][0][2]=A[1][1]; q.push({1,1,0,2});
int ans=0;
while (!q.empty())
{
auto [x,y,a,b]=q.front(); q.pop();
if (x==n&&y==m) ans=max(ans,f[x][y][a][b]);
auto upt=[&](CI nx,CI ny,CI na,CI nb)
{
int val=A[nx][ny];
if ((b==0&&nb==1)||(b==1&&nb==0)) val=0;
if (f[nx][ny][na][nb]<f[x][y][a][b]+val)
{
f[nx][ny][na][nb]=f[x][y][a][b]+val;
q.push({nx,ny,na,nb});
}
};
if (x+1<=n) upt(x+1,y,a,2);
if (y+1<=m) upt(x,y+1,a,1);
if (a==0&&y>1) upt(x,y-1,1,0);
}
printf("%lld\n",ans);
}
return 0;
}
D. Money in the Hat
徐神推式子后化简发现答案就是
预处理调和级数即可
#include <bits/stdc++.h>
using llsi = long long signed int;
constexpr int $n = 1000006;
constexpr llsi mod = 998244353;
constexpr llsi ksm(llsi a, llsi b) {
llsi c = 1;
while(b) {
if(b & 1) c = c * a % mod;
a = a * a % mod;
b >>= 1;
}
return c;
}
llsi fac[$n], facinv[$n];
llsi H[$n];
llsi inv(llsi a) {
return facinv[a] * fac[a - 1] % mod;
}
void prep(llsi n = 1000003) {
fac[0] = 1;
for(int i = 1; i <= n; ++i) fac[i] = fac[i - 1] * i % mod;
facinv[n] = ksm(fac[n], mod - 2);
for(int i = n; i >= 1; --i) facinv[i - 1] = facinv[i] * i % mod;
H[0] = 0;
for(int i = 1; i <= n; ++i) H[i] = (H[i - 1] + inv(i)) % mod;
return ;
}
llsi C(llsi a, llsi b) {
return fac[a] * facinv[b] % mod * facinv[a - b] % mod;
}
int main() {
std::ios::sync_with_stdio(false);
prep();
int T; std::cin >> T; while(T--) {
llsi n; std::cin >> n;
llsi ans = (n + 1 + mod - llsi(n + 1) * inv(n) % mod * (H[n + 1] - 1) % mod) % mod;
std::cout << ans << char(10);
}
return 0;
}
E. Gambling
先将两个数都除去它们的 \(\gcd\),不难发现任何时刻出现一对奇偶性不同的数则一定会成环
由于状态之间没有本质区别,因此后面的局面贡献一定为 \(1+\frac{1}{2}+\frac{1}{4}+\cdots=2\),简单记搜即可
#include <bits/stdc++.h>
using llsi = long long signed int;
constexpr llsi mod = 998244353;
constexpr llsi ksm(llsi a, llsi b) {
llsi c = 1;
while(b) {
if(b & 1) c = c * a % mod;
a = a * a % mod;
b >>= 1;
}
return c;
}
constexpr llsi inv2 = ksm(2, mod - 2);
void step(llsi &a, llsi &b) {
if(a < b) std::swap(a, b);
a -= b; b += b;
if(a < b) std::swap(a, b);
llsi g = std::__gcd(a, b);
a /= g, b /= g;
return ;
}
llsi solve(llsi a, llsi b) {
if(a == 0 || b == 0) return 0;
if(a == b) return 1;
if((a & 1) + (b & 1) == 1) return 2;
step(a, b);
return (1 + inv2 * solve(a, b)) % mod;
}
int main() {
std::ios::sync_with_stdio(false);
int T; std::cin >> T;
while(T--) {
llsi a, b, c, d;
std::cin >> a >> b;
llsi g = std::__gcd(a, b); a /= g; b /= g;
std::cout << solve(a, b) << char(10);
}
return 0;
}
G. Road Trip
序列上的原问题解决方案是从一边开始贪心分组,不难发现这个贪心从两边同时往里做也是成立的
因此对于树上路径,可以把两个端点都跳到距离 LCA 很近的位置,再暴力判断中间剩下的部分
具体地,预处理每个点向上的下一个划分点,用倍增维护后即可;此时只要判中间那段的长度与 \(c\) 的大小关系即可
#include<cstdio>
#include<iostream>
#include<vector>
#define int long long
#define RI register int
#define CI const int&
using namespace std;
const int N=200005;
int t,n,q,c,dis[N],dep[N],anc[N][20],f[N][20]; vector <pair <int,int>> v[N];
inline void DFS(CI now,CI fa,vector <int>& path)
{
anc[now][0]=fa; dep[now]=dep[fa]+1;
for (RI i=0;i<19;++i)
if (anc[now][i]) anc[now][i+1]=anc[anc[now][i]][i]; else break;
path.push_back(now);
int l=0,r=(int)path.size()-1,res=-1;
while (l<=r)
{
int mid=l+r>>1;
if (dis[now]-dis[path[mid]]<=c) res=mid,r=mid-1; else l=mid+1;
}
f[now][0]=path[res];
for (RI i=0;i<19;++i)
if (f[now][i]) f[now][i+1]=f[f[now][i]][i]; else break;
for (auto [to,w]:v[now])
{
if (to==fa) continue;
dis[to]=dis[now]+w;
DFS(to,now,path);
}
path.pop_back();
}
inline int getLCA(int x,int y)
{
if (dep[x]<dep[y]) swap(x,y);
for (RI i=19;i>=0;--i)
if (dep[anc[x][i]]>=dep[y]) x=anc[x][i];
if (x==y) return x;
for (RI i=19;i>=0;--i)
if (anc[x][i]!=anc[y][i]) x=anc[x][i],y=anc[y][i];
return anc[x][0];
}
inline int jump(int& x,CI y)
{
int res=0;
for (RI i=19;i>=0;--i)
if (dep[f[x][i]]>dep[y]) x=f[x][i],res+=(1LL<<i);
return res;
}
signed main()
{
for (scanf("%lld",&t);t;--t)
{
scanf("%lld%lld%lld",&n,&q,&c);
for (RI i=1;i<=n;++i)
{
v[i].clear();
for (RI j=0;j<20;++j)
anc[i][j]=f[i][j]=0;
}
for (RI i=1;i<n;++i)
{
int x,y,z; scanf("%lld%lld%lld",&x,&y,&z);
v[x].push_back({y,z}); v[y].push_back({x,z});
}
vector <int> path; dis[1]=0; DFS(1,0,path);
while (q--)
{
int x,y; scanf("%lld%lld",&x,&y);
int fa=getLCA(x,y),ans=0;
ans+=jump(x,fa); ans+=jump(y,fa);
int len=dis[x]+dis[y]-2LL*dis[fa];
if (len==0) ans+=0; else
if (len<=c) ans+=1; else ans+=2;
printf("%lld\n",ans-1);
}
}
return 0;
}
H. Decent Path Around Bajtów
队友说只要直接记搜一下就行,因为状态不成环所以不会出问题,但不知道为什么写挂了
I. Random Remainders
先给所有数排序,小的模大的这种情况很 trivial,只考虑固定 \(a_i\) 时它后面的 \(\sum_{j=i+1}^n (a_j\bmod a_i)^2\) 怎么计算
很容易想到把取模变成减去若干倍的 \(a_i\),因为所有数随机生成,任意两个数的商的值期望是 \(\log\) 级别的
因此可以直接二分 boundary,把倍数相同的 \(a_j\) 区间找出来一起处理,此时推一下式子发现只要维护简单的前缀和与前缀平方和即可
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MOD = 998244353;
void inc(int &x, int a) {if ((x+=a)>=MOD) x-=MOD;}
int sqr(int x) { return x*x%MOD; }
const int N = 2e5+5;
int n, A[N], sfx[N], sfx2[N];
void solve() {
cin >> n;
for (int i=1; i<=n; ++i) cin >> A[i];
sort(A+1, A+n+1);
sfx[n+1] = sfx2[n+1] = 0;
for (int i=n; i>0; --i) sfx[i] = (sfx[i+1] + A[i]%MOD)%MOD, sfx2[i] = (sfx2[i+1] + sqr(A[i]%MOD))%MOD;
int res = 0;
for (int i=n-1; i>0; --i) {
inc(res, (n-i)*sqr(A[i]%MOD)%MOD);
int val = A[i];
int lst = i;
while (1) {
int id = lower_bound(A+1, A+n+1, val+A[i]) - A;
// printf("lst=%lld id=%lld\n", lst, id);
int a = (sfx2[lst]-sfx2[id]+MOD)%MOD;
int b = 2 * ((sfx[lst]-sfx[id]+MOD)%MOD) * (val%MOD) %MOD;
int c = (id-lst)*sqr(val%MOD)%MOD;
// cout << a << ' ' << b << ' ' << c << '\n';
inc(res, (a-b+c+MOD)%MOD);
lst = id;
val += A[i];
if (id == n+1) break;
}
}
cout << res << '\n';
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0);
int T; cin >> T; while (T--) solve();
return 0;
}
J. Sumotonic Sequences
由于徐神做过 CCPC2023 Final 的 A,因此知道关键结论,这题就很简单
一个序列能拆分成题中所述的序列的充要条件为,求出原序列的差分数组 \(d_i=a_i-a_{i-1}\),合法当且仅当 \(a_1+\sum_{i=2}^n [d_i<0] d_i\ge 0\)
考虑一次修改操作对 \(\{d_i\}\) 的影响,即 \(d_p+=s,d_{p+1\sim q}+=d,d_{q+1}-=s+(p-q)\times d\),我们要求的是序列每次操作完后所有小于 \(0\) 的数之和
乍一看不好处理,但结合数据范围发现绝大部分操作都是在加正数,每次最多把一个数变成负数
因此如果我们把每个从负变成正的位置的贡献暴力处理,复杂度也是 \(O((n+q)\log n)\)级别的,故直接在线段树上维护即可
#include<cstdio>
#include<iostream>
#define int long long
#define RI register int
#define CI const int&
using namespace std;
const int N=200005,INF=1e18;
int t,n,k,a[N];
class Segment_Tree
{
private:
int val[N<<2],neg_mx[N<<2],neg_cnt[N<<2],neg_sum[N<<2],tag[N<<2];
inline void pushup(CI now)
{
neg_mx[now]=max(neg_mx[now<<1],neg_mx[now<<1|1]);
neg_cnt[now]=neg_cnt[now<<1]+neg_cnt[now<<1|1];
neg_sum[now]=neg_sum[now<<1]+neg_sum[now<<1|1];
}
inline void apply(CI now,CI mv,CI cnt)
{
val[now]+=mv; neg_mx[now]+=mv; neg_sum[now]+=mv*cnt; tag[now]+=mv;
}
inline void pushdown(CI now)
{
if (tag[now]) apply(now<<1,tag[now],neg_cnt[now<<1]),apply(now<<1|1,tag[now],neg_cnt[now<<1|1]),tag[now]=0;
}
public:
#define TN CI now=1,CI l=2,CI r=n
#define LS now<<1,l,mid
#define RS now<<1|1,mid+1,r
inline void build(TN)
{
val[now]=tag[now]=0;
if (l==r)
{
val[now]=a[l];
if (val[now]<0) neg_cnt[now]=1,neg_sum[now]=neg_mx[now]=val[now];
else neg_cnt[now]=neg_sum[now]=0,neg_mx[now]=-INF;
return;
}
int mid=l+r>>1; build(LS); build(RS); pushup(now);
}
inline void modify_pos(CI beg,CI end,CI mv,TN)
{
if (beg<=l&&r<=end)
{
if (neg_mx[now]+mv<0) return apply(now,mv,neg_cnt[now]);
if (l==r)
{
val[now]+=mv;
if (val[now]<0) neg_cnt[now]=1,neg_sum[now]=neg_mx[now]=val[now];
else neg_cnt[now]=neg_sum[now]=0,neg_mx[now]=-INF;
return;
}
}
int mid=l+r>>1; pushdown(now);
if (beg<=mid) modify_pos(beg,end,mv,LS);
if (end>mid) modify_pos(beg,end,mv,RS);
pushup(now);
}
inline void modify_neg(CI pos,CI mv,TN)
{
if (l==r)
{
val[now]+=mv;
if (val[now]<0) neg_cnt[now]=1,neg_sum[now]=neg_mx[now]=val[now];
else neg_cnt[now]=neg_sum[now]=0,neg_mx[now]=-INF;
return;
}
int mid=l+r>>1; pushdown(now);
if (pos<=mid) modify_neg(pos,mv,LS); else modify_neg(pos,mv,RS);
pushup(now);
}
inline int query(void)
{
return neg_sum[1];
}
#undef TN
#undef LS
#undef RS
}SEG;
signed main()
{
for (scanf("%lld",&t);t;--t)
{
scanf("%lld%lld",&n,&k);
for (RI i=1;i<=n;++i) scanf("%lld",&a[i]);
for (RI i=n;i>=2;--i) a[i]-=a[i-1];
// for (RI i=1;i<=n;++i) printf("%lld%c",a[i]," \n"[i==n]);
SEG.build(); puts(a[1]+SEG.query()>=0?"YES":"NO");
while (k--)
{
int l,r,s,d;
scanf("%lld%lld%lld%lld",&l,&r,&s,&d);
if (l==1) a[1]+=s;
if (l!=1) SEG.modify_pos(l,l,s);
if (l+1<=r) SEG.modify_pos(l+1,r,d);
if (r+1<=n) SEG.modify_neg(r+1,-(s+(r-l)*d));
puts(a[1]+SEG.query()>=0?"YES":"NO");
}
}
return 0;
}
L. Empty Triangles
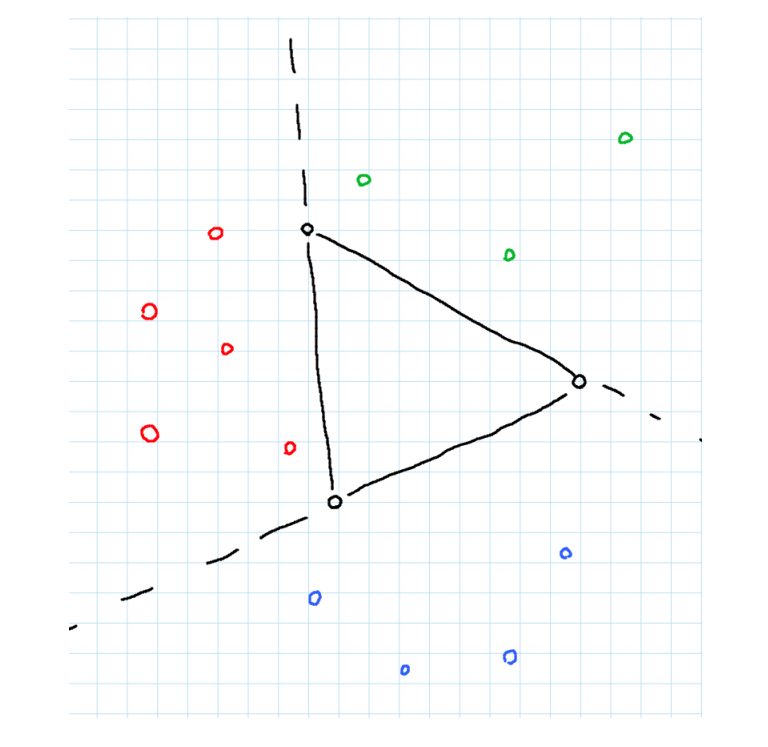
借用题解里的图,因为任意三点不共线,因此判断三角形内部有没有点可以转化为看图中三部分的点数量之和是否为 \(n-3\)
把以每个点为起点的向量极角排序后,询问时直接二分即可
#include<bits/stdc++.h>
using namespace std;
// #define int long long
#define LL long long
struct Pt {
int x, y;
int qd = -1;
int quad() const {
if (x > 0 && y >= 0) return 1;
if (x <= 0 && y > 0) return 2;
if (x < 0 && y <= 0) return 3;
if (x >= 0 && y < 0) return 4;
}
LL crs(const Pt &a) const {return 1LL*x*a.y-1LL*y*a.x;}
Pt operator-(const Pt &a) const {return Pt{x-a.x, y-a.y};}
Pt operator~() const {return Pt{-x, -y, qd+2};}
bool operator<(const Pt &a) const {
if (qd != a.qd) return qd < a.qd;
else return this->crs(a) > 0;
}
};
const int N = 5005;
Pt pt[N];
vector<Pt> vec[N];
void solve() {
int n, q; cin >> n >> q;
for (int i=1; i<=n; ++i) {
int x, y; cin >> x >> y;
pt[i].x = x; pt[i].y = y;
vec[i].clear();
}
for (int i=1; i<=n; ++i) {
for (int j=1; j<=n; ++j) if (j!= i) {
Pt v = pt[j]-pt[i];
v.qd = v.quad();
vec[i].push_back(v);
v.qd += 4;
vec[i].push_back(v);
}
sort(vec[i].begin(), vec[i].end());
}
while (q--) {
int id[3]; cin >> id[0] >> id[1] >> id[2];
int res = 0;
for (int i=0; i<3; ++i) {
Pt v1 = pt[id[(i+1)%3]] - pt[id[i]];
Pt v2 = pt[id[(i+2)%3]] - pt[id[i]];
if (v1.crs(v2) <= 0) swap(v1, v2);
v1.qd = v1.quad();
v2.qd = v2.quad();
if (v2.qd < v1.qd) v2.qd += 4;
auto it1 = lower_bound(vec[id[i]].begin(), vec[id[i]].end(), v1);
auto it2 = lower_bound(vec[id[i]].begin(), vec[id[i]].end(), v2);
auto it3 = lower_bound(vec[id[i]].begin(), vec[id[i]].end(), ~v1);
auto it4 = lower_bound(vec[id[i]].begin(), vec[id[i]].end(), ~v2);
res += (it2 - it1) + (it4 - it3);
}
// cout << "res = " << res << '\n';
cout << (res == n ? "YES\n" : "NO\n");
}
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0);
int T; cin >> T; while (T--) solve();
return 0;
}
Postscript
答应我以后别一场比赛 AC 率不到 30% 了好吗


 浙公网安备 33010602011771号
浙公网安备 33010602011771号