The 1st Universal Cup. Stage 22: Shaanxi
Preface
时隔一周之后难得开了场训练,然后犯了一堆弱智错误给自己搞红温了,最后感觉啥难题也没写就混着混着就结束了
赛后想补题经典找不到题解,只搜到哥哥的题解结果搞不懂细节还是写不来一点,直接开摆
D. Alice and Bob
首先博弈部分的结论很好猜,若第一次操作开头的数为 \(x\),则若 \(p_1\sim p_x\) 都 \(\ge x\) 则先手必败
证明的话考虑满足上述条件后手一定能把 \(x\) 换回开头;否则先手可以把最小的数换到开头然后规约为上述情况
统计方案数的话就直接枚举 \(p_1\) 的值即可,式子很好推
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=1e7+5,mod=998244353;
int n,fact[N],ifac[N];
inline int quick_pow(int x,int p=mod-2,int mul=1)
{
for (;p;p>>=1,x=1LL*x*x%mod) if (p&1) mul=1LL*mul*x%mod; return mul;
}
inline void init(CI n)
{
fact[0]=1; for (RI i=1;i<=n;++i) fact[i]=1LL*fact[i-1]*i%mod;
ifac[n]=quick_pow(fact[n]); for (RI i=n-1;i>=0;--i) ifac[i]=1LL*ifac[i+1]*(i+1)%mod;
}
inline int C(CI n,CI m)
{
if (n<0||m<0||n<m) return 0;
return 1LL*fact[n]*ifac[m]%mod*ifac[n-m]%mod;
}
int main()
{
scanf("%d",&n); init(n); int ans=0;
for (RI i=1;i<=n;++i) (ans+=1LL*C(n-i,i-1)*fact[i-1]%mod*fact[n-i]%mod)%=mod;
return printf("%d",ans),0;
}
G. Teleport
徐神的大手,用我闻所未闻的神秘建边淦飞了这个题
考虑一直用 teleport 操作的话会得到 \(n\) 条长度为 \(n\) 且互不相交的路径,路径上每个点可以跳到接下来的 \([1,k]\) 范围内的点,剩下四联通的走法就暴力连边
考虑优化 teleport 的建图,我们把长为 \(n\) 的点每 \(k\) 个分成一组,同时建两排辅助点,一排往后一排往前,但不连跨过组的边,大致结构如下:
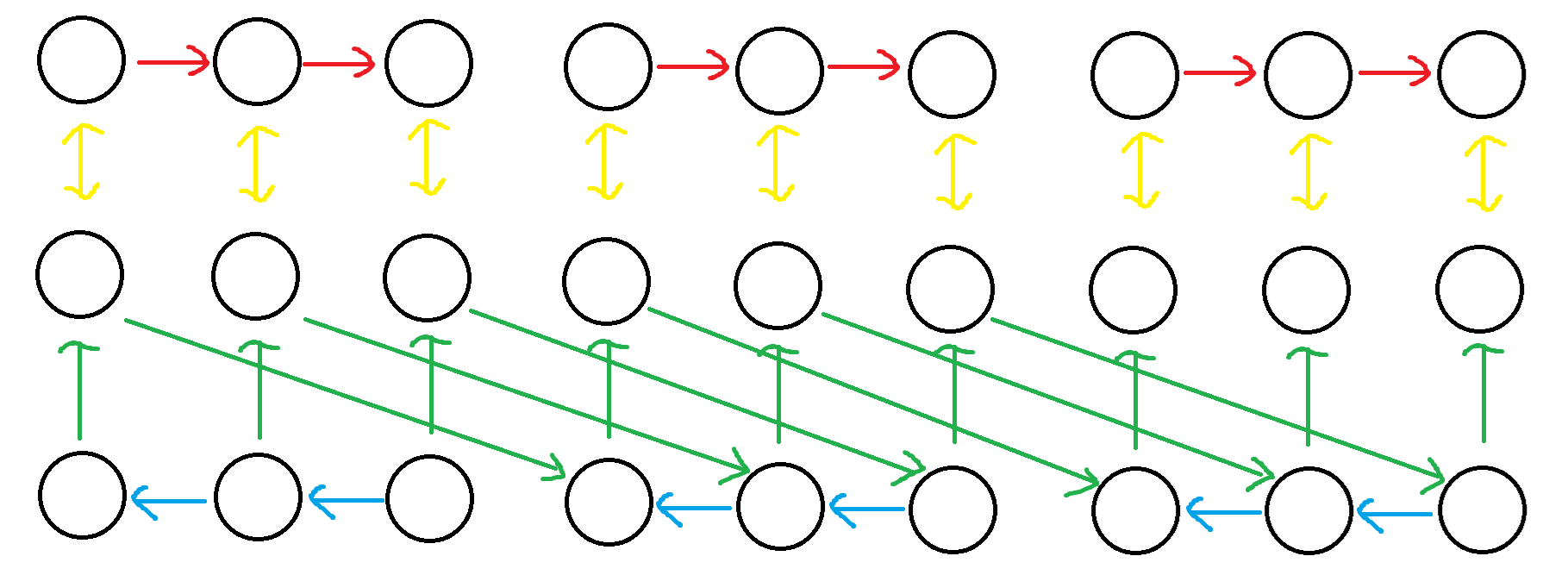
(中间一排是原本的点,假设 \(n=9,k=3\),此时每个点都和后面 \([1,k]\) 范围的点连通)
然后就跑个最短路即可,复杂度 \(O(n^2)\)
#include <bits/stdc++.h>
int n, k;
int dis[3][5000][5000];
std::string ms[5000];
std::deque<std::tuple<short, short, short>> q;
inline short get_id(short x, short y) { return std::min(x, y) * 2 + (y > x); }
inline std::pair<short, short> get_pth_next(short x, short y, short p) {
short fx = x, fy = y, bid = get_id(x, y);
x += p >> 1, y += p >> 1;
if(p & 1) std::swap(x, y), y++;
if(x < n && y < n) return { x, y };
if(fx < fy) std::swap(fx, fy), fy++;
short dt = n - 1 - fx;
fx += dt, fy += dt;
if(get_id(fx, fy) / k == bid / k) return { -1, -1 };
return { fx, fy };
}
inline std::pair<short, short> get_pth_prev(short x, short y, short p) {
x -= p >> 1, y -= p >> 1;
if(p & 1) std::swap(x, y), x--;
return { x, y };
}
void update(short type, std::pair<short, short> ss, int d, int delta) {
auto [nx, ny] = ss;
if(nx < 0 || nx >= n || ny < 0 || ny >= n) return ;
if(type == 0 && ms[nx][ny] == '*') return ;
if(d + delta >= dis[type][nx][ny]) return ;
dis[type][nx][ny] = d + delta;
if(delta == 1) q.emplace_back(type, nx, ny);
else q.emplace_front(type, nx, ny);
return ;
}
int hkr[10000];
std::ostream& operator <<(std::ostream &out, const std::pair<short, short> &p) {
return out << p.first << " " << p.second;
}
int main() {
std::ios::sync_with_stdio(false);
memset(dis, 0x3f, sizeof(dis));
std::cin >> n >> k;
// for(int i = 0; i < n; ++i) for(int j = 0; j < n; ++j) std::cerr << get_id(i, j) << char(j == n - 1 ? 10 : 32);
// std::cout << get_pth_next(0, 2, 3) << char(10);
hkr[0] = 0;
for(int i = 1; i < 10000; ++i) hkr[i] = (hkr[i - 1] + 1) % k;
for(int i = 0; i < n; ++i) std::cin >> ms[i];
for(int i = 0; i < n; ++i) for(int j = 0; j < i; ++j) std::swap(ms[i][j], ms[j][i]);
q.push_back({0, 0, 0});
if(ms[0][0] != '*') dis[0][0][0] = 0;
while(q.size()) {
auto [type, x, y] = q.front(); q.pop_front();
short id = get_id(x, y);
int d = dis[type][x][y];
switch(type) {
case 0:
for(auto [dx, dy]: (short[4][2]){0, 1, 0, -1, 1, 0, -1, 0})
update(0, std::make_pair(x + dx, y + dy), d, 1);
update(1, get_pth_next(x, y, 0), d, 1);
update(2, get_pth_next(x, y, k), d, 1);
break;
case 1:
if(hkr[id] + 1 != k) update(1, get_pth_next(x, y, 1), d, 0);
update(0, std::make_pair(x, y), d, 0);
break;
case 2:
if(hkr[id] != 0) update(2, get_pth_prev(x, y, 1), d, 0);
update(0, std::make_pair(x, y), d, 0);
break;
default:
abort();
}
}
// for(int type = 0; type < 3; ++type) {
// for(int i = 0; i < n; ++i) for(int j = 0; j < n; ++j)
// std::cerr << (dis[type][i][j] >= 114514 ? "*" : std::format("{}", dis[type][i][j])) << char(j == n - 1 ? 10 : 32);
// std::cerr << "==================================\n";
// }
if(dis[0][n - 1][n - 1] > n * n * 3) std::cout << "-1\n";
else std::cout << dis[0][n - 1][n - 1] << char(10);
return 0;
}
H. Function
倒着推感觉不太可做,我们不妨定义一个新函数 \(g(x)\),初值为 \(g(x)=0\),转移为:
经过证明打表我们发现 \(g(n)\) 和题目中 \(f(1)\) 的值是相同的,而这个式子一眼用除法分块优化,复杂度 \(O(n^\frac{3}{4})\)
#include<cstdio>
#include<iostream>
#include<cassert>
#include<unordered_map>
#define RI register int
#define CI const int&
using namespace std;
const int mod=998244353;
int n; unordered_map <int,int> g;
inline int G(CI n)
{
if (g.count(n)) return g[n]; int ret=1;
for (RI l=2,r;l<=n&&l<=20210926;l=r+1)
{
r=min(20210926,n/(n/l));
(ret+=1LL*(r-l+1)*G(n/l)%mod)%=mod;
}
return g[n]=ret;
}
int main()
{
scanf("%d",&n);
/*for (int n=1;n<=1000;++n)
{
static int f[1005],g[1005];
for (RI x=1000;x>=1;--x)
{
f[x]=1;
for (RI k=2;k<=20210926;++k)
{
long long y=x*k;
if (y>n) break;
(f[x]+=f[y])%=mod;
}
}
for (RI x=1;x<=1000;++x)
{
g[x]=1;
for (RI k=2;k<=20210926;++k)
{
int y=x/k;
if (y==0) break;
(g[x]+=g[y])%=mod;
}
}
assert(f[1]==g[n]);
//printf("%d %d\n",f[1],g[n]);
}*/
return printf("%d",G(n)),0;
}
I. Digit
这种题一眼有效状态很少,直接大力对所有有用的状态记忆化搜索一下即可
稍微推一下期望的式子会发现因为是 DAG 所有转移的自环可以直接移项去除,实现的话注意一些常数
#include<bits/stdc++.h>
using namespace std;
#define int unsigned long long
const int MOD = 998244353;
void inc(int &x, int a) {if ((x+=a)>=MOD) x-=MOD;}
void mul(int &x, int a) {x=x*a%MOD;}
int powe(int x, int p) {
int res=1;
while (p>0) { if (p&1) mul(res, x); mul(x, x); p>>=1;}
return res;
}
int n, lim;
unordered_map<int, int> mp;
int inv1[30], inv2[30][30];
vector<int> digit(int x) {
vector<int> vec(10);
while (x>0) {
++vec[x%10];
x /= 10;
}
return vec;
}
int f(int x) {
if (x > lim) return 0;
if (mp.count(x)) return mp[x];
vector<int> vec = digit(x);
int res = 0;
for (int i=0; i<=9; ++i) res += vec[i];
// printf("x=%llu res=%llu\n", x, res);
int ans = 0;
for (int i=2; i<=10; ++i) if (vec[i-1]>0) {
int tmp = 0;
inc(tmp, (vec[i-1]*inv1[res]%MOD*f(x*i))%MOD);
// printf("x=%llu i=%llu vec=%llu tmp=%llu\n", x, i, vec[i-1], tmp);
inc(ans, tmp);
}
inc(ans, 1);
if (vec[0] > 0) mul(ans, inv2[vec[0]][res]);
return mp[x] = ans;
}
int solve() {
cin >> n >> lim;
mp.clear();
// printf("n=%llu\n", n);
int res = f(n);
// for (auto [x, y] : mp) printf("(%llu %llu)", x, y); puts("");
return res;
}
signed main() {
// printf("%llu\n", powe(2, MOD-2));
ios::sync_with_stdio(0); cin.tie(0);
for (int i=1; i<=20; ++i) inv1[i] = powe(i, MOD-2);
for (int i=1; i<=20; ++i) for (int j=i; j<=20; ++j) inv2[i][j] = powe((MOD+1 - i*powe(j, MOD-2)%MOD), MOD-2);
int t; cin >> t; while (t--) cout << solve() << '\n';
return 0;
}
J. Leaves
很一眼的题,令 \(f_{i,j}\) 表示处理了点 \(i\) 的子树,共用了 \(j\) 次交换操作能得到的最小的字典序
由树上背包的姿势只看这两维是 \(O(n^2)\) 的,但是由于合并两个子树时还有 \(O(n)\) 的开销,因此最后总复杂度 \(O(n^3)\)
实现的时候注意请看没用的状态不然会 MLE
#include<cstdio>
#include<iostream>
#include<vector>
#define RI register int
#define CI const int&
using namespace std;
const int N=1005,INF=1e9+5;
int n,m,tp,l[N],r[N],a[N],sz[N]; vector <int> f[N][N/2];
inline void DFS(CI now=1)
{
if (a[now])
{
f[now][0]={a[now]}; f[now][1]={INF};
return;
}
int ls=l[now],rs=r[now]; sz[now]=1;
DFS(ls); DFS(rs); sz[now]+=sz[ls]+sz[rs];
for (RI i=0;i<=min(m,sz[now]);++i) f[now][i]={INF};
auto merge=[&](vector <int>& A,vector <int>& B)
{
vector <int> vec=A;
for (auto& x:B) vec.push_back(x);
return vec;
};
for (RI p=0;p<=min(m,sz[ls]);++p)
for (RI q=0;q<=min(m-p,sz[rs]);++q)
{
f[now][p+q]=min(f[now][p+q],merge(f[ls][p],f[rs][q]));
if (p+q+1<=m) f[now][p+q+1]=min(f[now][p+q+1],merge(f[rs][q],f[ls][p]));
}
for (RI i=2;i<=min(m,sz[now]);++i) f[now][i]=min(f[now][i],f[now][i-2]);
for (RI i=0;i<=min(m,sz[ls]);++i) f[ls][i].shrink_to_fit();
for (RI i=0;i<=min(m,sz[rs]);++i) f[rs][i].shrink_to_fit();
}
int main()
{
scanf("%d%d",&n,&m);
for (RI i=1;i<=n;++i)
{
scanf("%d",&tp);
if (tp==1) scanf("%d%d",&l[i],&r[i]);
else scanf("%d",&a[i]);
}
DFS(); for (auto x:f[1][m]) printf("%d ",x);
return 0;
}
K. water235
签到,先放一个对角线,然后多出来的维度每隔一个放即可
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+5;
bool flag;
int ans[N], c;
signed main() {
ios::sync_with_stdio(0); cin.tie(0);
int n, m; cin >> n >> m;
if (n>m) swap(n, m), flag=true;
for (int i=0; i<n; ++i) ans[i*m+i]=1;
for (int i=n; i<m; ++i) if ((i-n)%2==1) ans[i]=1;
if (n<m) ans[m-1]=1;
cout << n + (m-n+1)/2 << '\n';
if (!flag) {
for (int i=0; i<n; ++i) {
for (int j=0; j<m; ++j) cout << ans[i*m+j] << ' ';
cout << '\n';
}
} else {
for (int j=0; j<m; ++j) {
for (int i=0; i<n; ++i) cout << ans[i*m+j] << ' ';
cout << '\n';
}
}
return 0;
}
L. Square
神秘找规律题,手玩可以发现以下两个关键结论:
- \([1],[2,3],[4,6],[7,10],\dots\) 每一段内的数增量相同,且段长依次加 \(1\);
- 每个数距离其所在段右端点的距离保持恒定,例如 \(2\to 5\to 9\),距离所在段右端点的距离恒为 \(1\);
因此我们二分求出 \(x,y\) 的所在段以及距离右端点的距离后,分类讨论一下减一操作是在开头还是结束即可
#include<bits/stdc++.h>
using namespace std;
#define int long long
using pii = pair<int, int>;
#define ft first
#define sd second
pii find(int x) {
auto calc = [&](int x) -> int{ return (1+x)*x/2;};
int L=1, R=2e9+5;
while (L<R) {
int M=L+(R-L)/2;
if (calc(M)>=x) R=M;
else L=M+1;
}
return {L, calc(L)};
}
int solve() {
int x, y; cin >> x >> y;
if (x>y) return x-y;
auto [v1, res1] = find(x);
auto [v2, res2] = find(y);
int pos = res2 - (res1-x);
if (pos < y) {
int ans = 0;
res1 -= v1;
--v1;
return x-(res1-(res2-y)) + v2-v1;
} else return v2 - v1 + pos - y;
}
signed main() {
ios::sync_with_stdio(0); cin.tie(0);
int t; cin >> t; while (t--) cout << solve() << '\n';
return 0;
}
M. Delete the Tree
事到如今才发现我用了整个算竞生涯的点分治板子竟然有锅,不过只要不是在赛场上发现的都可以接受
这题思路其实很好想,就是求出点分树后按深度从下往上把同层的点一起处理即可
#include<cstdio>
#include<iostream>
#include<vector>
#include<cassert>
#define RI register int
#define CI const int&
using namespace std;
const int N=505;
int n,x,y,Rt; vector <int> v[N],nv[N],bkt[N];
namespace Point_Divide
{
int rt,ots,sz[N],mx[N]; bool vis[N];
inline void getrt(CI now=1,CI fa=0)
{
sz[now]=1; mx[now]=0;
for (auto to:v[now]) if (to!=fa&&!vis[to])
{
getrt(to,now); sz[now]+=sz[to];
mx[now]=max(mx[now],sz[to]);
}
if (mx[now]=max(mx[now],ots-sz[now]),mx[now]<mx[rt]) rt=now;
}
inline void solve(int now)
{
vis[now]=1; for (auto to:v[now]) if (!vis[to])
mx[rt=0]=n,ots=sz[to],getrt(to,now),getrt(rt,0),nv[now].push_back(rt),solve(rt);
}
inline void divide(CI n)
{
mx[rt=0]=n; ots=n; getrt(); Rt=rt; solve(rt);
}
}
inline void DFS(CI now=Rt,CI d=1)
{
bkt[d].push_back(now);
for (auto to:nv[now]) DFS(to,d+1);
}
int main()
{
scanf("%d",&n);
for (RI i=1;i<n;++i) scanf("%d%d",&x,&y),v[x].push_back(y),v[y].push_back(x);
Point_Divide::divide(n); DFS(); int mxd=-1;
for (RI i=1;i<=n;++i) if (!bkt[i].empty()) mxd=i;
printf("%d\n",mxd);
assert(mxd<=10);
for (RI i=mxd;i>=1;--i)
{
printf("%d ",bkt[i].size());
for (auto x:bkt[i]) printf("%d ",x);
putchar('\n');
}
return 0;
}
Postscript
感觉这场最大收获就是给板子捉了个虫,只要不在赛场上发现的板子出锅都是正收益啊


 浙公网安备 33010602011771号
浙公网安备 33010602011771号