0.递归

0.递归

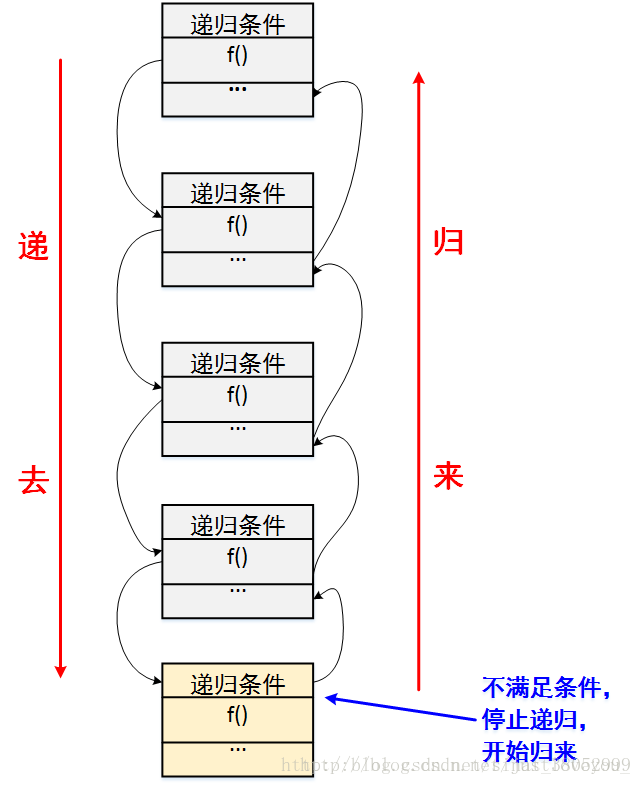
递归就是有去（递去）有回（归来），如下图所示。“有去”是指：递归问题必须可以分解为若干个规模较小，与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决，就像上面例子中的钥匙可以打开后面所有门上的锁一样；“有回”是指 : 这些问题的演化过程是一个从大到小，由近及远的过程，并且会有一个明确的终点(临界点)，一旦到达了这个临界点，就不用再往更小、更远的地方走下去。最后，从这个临界点开始，原路返回到原点，原问题解决。

递归的三要素：

1、明确递归终止条件；

2、给出递归终止时的处理办法；

3、提取重复的逻辑，缩小问题规模。

 

1). 明确递归终止条件

　　 我们知道，递归就是有去有回，既然这样，那么必然应该有一个明确的临界点，程序一旦到达了这个临界点，就不用继续往下递去而是开始实实在在的归来。换句话说，该临界点就是一种简单情境，可以防止无限递归。

2). 给出递归终止时的处理办法

　　 我们刚刚说到，在递归的临界点存在一种简单情境，在这种简单情境下，我们应该直接给出问题的解决方案。一般地，在这种情境下，问题的解决方案是直观的、容易的。

3). 提取重复的逻辑，缩小问题规模*

　　 我们在阐述递归思想内涵时谈到，递归问题必须可以分解为若干个规模较小、与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决。从程序实现的角度而言，我们需要抽象出一个干净利落的重复的逻辑，以便使用相同的方式解决子问题

模型一： 在递去的过程中解决问题

function recursion(大规模){
    if (end_condition){      // 明确的递归终止条件
        end;   // 简单情景
    }else{            // 在将问题转换为子问题的每一步，解决该步中剩余部分的问题
        solve;                // 递去
        recursion(小规模);     // 递到最深处后，不断地归来
    }
}

模型二： 在归来的过程中解决问题

function recursion(大规模){
    if (end_condition){      // 明确的递归终止条件
        end;   // 简单情景
    }else{            // 先将问题全部描述展开，再由尽头“返回”依次解决每步中剩余部分的问题
        recursion(小规模);     // 递去
        solve;                // 归来
    }
}