记 第一次模拟
2020、12、1
人生第一次参加模拟:-)
学了这么多月,总有了收获!!
———————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————第 一 题 :
计算系数
输入文件:factor.in
输出文件:factor.out
提交文件:factor.pas/cpp
时间限制:1S
空间限制:128M
题目描述:
给定一个多项式(ax + by)k,请求出多项式展开后xn ym项的系数。
输入格式:
共一行,包含 5 个整数,分别为a,b,k,n,m,每两个整数之间用一个空格隔开。
输出格式:
输出共 1 行,包含一个整数,表示所求的系数,这个系数可能很大,输出对10007 取
模后的结果。
样例输入:
1 1 3 1 2
样例输出:
3
数据范围
对于 30%的数据,有0≤k≤10;
对于 50%的数据,有a = 1,b = 1;
对于 100%的数据,有0≤k≤1,000,0≤n, m≤k,且n + m = k,0≤a,b≤1,000,000。
这道题要用杨辉三角是我没想到的!!!
typedef long long ll;
ll jc(ll m){
if(m == 0)return 0;
else{
m = m * jc(m - 1);
return m;
}
}
int quickpow(ll x,ll n){
ll res = 1;
if(n == 0) return 1;
while(n > 0){
if(n & 1)res = res * x % 10007;
x = x * x % 10007;
n >>= 1;
}
return res;
}
int main(){
// freopen("factor.in","r",stdin);
// freopen("factor.out","w",stdout);
ll a,b,k,m,n, p,h,q;
scanf("%lld %lld %lld %lld %lld",&a,&b,&k,&n,&m);
q = jc(k) / (jc(n) * jc(k - n)) % 10007;
p = quickpow(a,n) * quickpow(b,m);
h = q * p;
printf("%lld",h);
return 0;
}
上面呢,就是公式法,cki*an*bm
(cki=k!/[n! * (k-n)!])模拟的时候,我这个竟然忘了!!!!!
cj如我T-T
写出来之后也就20分,原因呢,就是因为用了阶乘加快速幂,超了1s,T L E警告!
那下面就看看正解,杨辉三角加快速幂!(牛蛙)
ps:某机房巨神杨辉三角打表,也是20分!!
——————分析过程——————
(x+y)¹=x + y
(x+y)²=x² + 2xy +y²
(x+y)³=x³ + 3x²y + 3xy² + y³
(x+y)4=x4 + 4x^3 y + 6x^2 y^2 + 4x y^3 + y^4
(x+y)5=x5 +5 x^4 y + 10 x^3 y^2 + 10 x^2 y^3 + 5 xy^4 + y^5
我们再把系数提出来:
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
我们就会惊奇的发现:
杨辉三角!惊喜意外!!!!!
//杨辉三角
using namespace std;
int x[1005][1005],a,b;
int main(){
x[2][1] = 1,x[2][2] = 1,x[1][1] = 1;
scanf("%d %d",&a,&b);
for(int i = 3;i <= a;i ++){
x[1][i] = 1;
x[i][i] = 1;
}
for(int i = 3;i <= a;i ++){
for(int j = 1; j <= i;j ++){
x[i][j] = x[i-1][j-1] + x[i-1][j];
}
}
printf("%d",x[a][b]);
return 0;
}
dangdangdangdang~
对于100%的数据,每一项的系数就是50分做法所对应的杨辉三角的值再乘(an)再乘(bm)!这点我们可以用快速幂来做。
define ll long long
define MOD 10007
define N 2100
define R register ll
ll a,b,k,n,m;
ll g[N][N];
inline void INIT()
{
g[1][1]=1;
for (R i=2;i<=k+1;i++)
{
for (R j=1;j<=i;j++)
{
g[i][j]=(g[i-1][j-1]%MOD+g[i-1][j]%MOD)%MOD;
}
}
}
inline ll mypow(ll aa,ll bb)
{
ll lh=aa;
for (R i=2;i<=bb;i++)
{
lh*=aa;
lh%=MOD;
}
return lh;
}
int main()
{
//freopen("factor.in","r",stdin);
//freopen("factor.out","w",stdout);
scanf("%lld%lld%lld%lld%lld",&a,&b,&k,&n,&m);
INIT();
printf("%lld",((((g[k+1][k-n+1]%MOD)mypow(a,n))%MOD)mypow(b,m))%MOD);
fclose(stdin);
fclose(stdout);
return 0;
}
缩进不太舒服,凑合一下[手动滑稽]
———————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————
第 二 题 :
汉诺塔问题
输入文件:hanoi.in
输出文件:hanoi.out
提交文件:hanoi.pas/cpp hanoi.exe
时间限制:1S
空间限制:128M
题目描述:
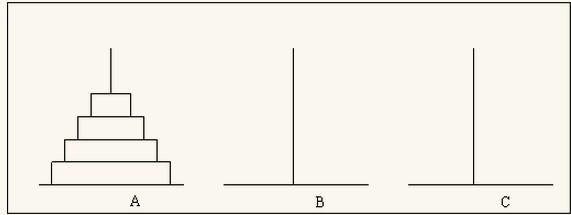
汉诺塔由编号为1到n大小不同的圆盘和三根柱子a,b,c组成。开始时,这n个圆盘由大到小依次套在a柱上,如图所示。要求把a柱上n个圆盘按下述规则移到c柱上:
(1)一次只能移一个圆盘,它必须位于某个柱子的顶部;
(2)圆盘只能在三个柱上存放;
(3)任何时刻不允许大盘压小盘。
将这n个盘子从a柱移动到c柱上,最少需要移动多少次?
输入格式:
第一行输入一个正整数n(1<=n<=30),表示圆盘的数量。
输出格式:
输出一个数表示最少需要移动的次数。
样例输入:
3
样例输出:
7
代码~~~
int hanoi(int a){
int sum = 1;
if(a == 1)return 1;
if(a != 1){
int s = hanoi(a - 1) * 2;
return sum + s;
}
}
int main(){
// freopen("hanoi.in","r",stdin);
// freopen("hanoi.out","w",stdout);
int a;
scanf("%d",&a);
printf("%d",hanoi(a));
return 0;
}
//得分:90
如果按递归写,会有超时现象,递归不行事!!
typedef long long ll;
//把long long用ll代替
ll quickpow(long long x,long long n){
ll res = 1;
while(n > 0){
if(n & 1) res = res * x;
x = x * x;
n >>= 1;//相当于n=n/2.二进制减最后一位
}
return res;
}
int main(){
// freopen("hanoi.in","r",stdin);
// freopen("hanoi.out","w",stdout);
int a;
scanf("%d",&a);
printf("%d",quickpow(2,a) - 1);
return 0;
}
这个方法是找规律,汉诺塔上,移动次数 = 2的n次方 - 1(n为盘子数量)
30过了!
———————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————
第 三 题 :
骨牌覆盖:
输入文件:domino.in
输出文件:domino.out
提交文件:domino.pas/cpp domino.exe
时间限制:1S
空间限制:128M
题目描述:
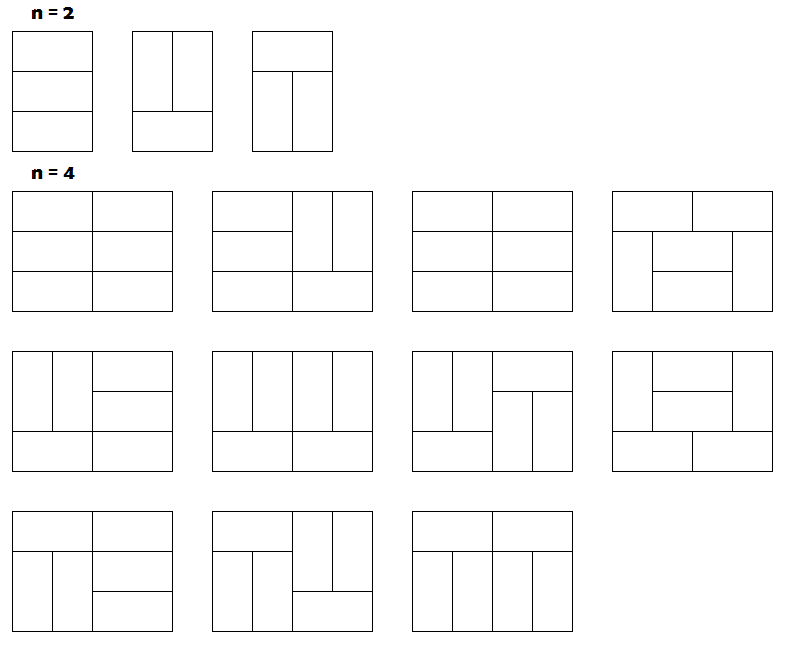
有2行n列的长方形方格,要求用n个1*2的骨牌铺满。有多少种铺法?
如n=3时有以下3种覆盖方法:
输入格式:
第一行输入一个正整数n(1<=n<=50)
输出格式:
输出一个整数表示方案数。
样例输入:
3
样例输出:
3
代码~~~
include
include
include
int main(){
freopen("domino.in","r",stdin);
freopen("domino.out","w",stdout);
long long f1 = 1,f2 = 1,fn;
int n;
scanf("%d",&n);
for(int i = 1;i <n;i ++){
fn = f1 + f2;
f1 = f2;
f2 = fn;
}
printf("%lld",fn);
return 0;
}
//当时 全 切 了!!
骨牌覆盖问题(2 * n)事实上就是一个递推斐波那契


 浙公网安备 33010602011771号
浙公网安备 33010602011771号