《大话数据结构》第9章 排序 9.7 堆排序(上)
9.7.1 堆结构介绍
我们前面讲到简单选择排序,它在待排序的n个记录中选择一个最小的记录需要比较n-1次。本来这也可以理解,查找第一个数据需要比较这么多次正常的,否则如何知道它是最小的记录。
可惜的是,这样的操作并没有把每一趟的比较结果保存下来,在后一趟的比较中,有许多比较在前一趟已经做过了,但由于前一趟排序时未保存这些比较结果,所以后一趟排序时又重复执行了这些比较操作,因而记录的比较次数较多。
如果可以做到每次在选择到最小的记录的同时,并根据比较对其他记录做出相应的调整,那样排序的总体效率就会非常高了。而堆排序(Heap Sort),就是对简单选择排序进行的一种改进,这种改进的效果是非常明显的。堆排序算法是Floyd和Williams在1964年共同发明的,同时,他们发明了堆这样的数据结构。
回忆一下我们小时候,特别是男同学,基本都玩过叠罗汉的恶作剧。通常都是先把某个要整的人按倒在地,然后大家就一拥而上扑了上去……后果?后果当然就是一笑了知,一个恶作剧而已。不过在西班牙的加泰罗尼亚地区,他们将叠罗汉视为了正儿八经的民族体育活动,如图9-7-1,可以想像当时场面的壮观。

叠罗汉运动是把人堆在一起,而我们这里要介绍的“堆”结构相当于把数字符号堆成一个塔型的结构。当然,这绝不是简单的堆砌。大家看图9-7-2,能够找到什么规律吗?
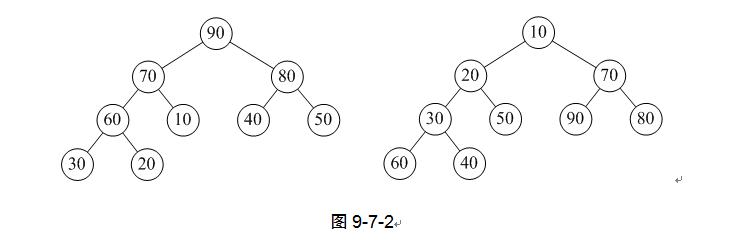
很明显,我们可以发现它们都是二叉树,如果观察仔细些,还能看出它们都是完全二叉树。左图中根结点是所有元素中最大的,右图的根结点是所有元素中最小的。再细看看,发现左图每个结点都比它的左右孩子要大,右图每个结点都比它的左右孩子要小。这就是我们要讲的堆结构。
堆是具有下列性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆(例如图9-7-2左图);或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆(例如图9-7-2右图)。
这里需要注意从堆的定义可知,根结点一定是堆中所有结点最大(小)者。较大(小)的结点靠近根结点(但也不绝对,比如右图小顶堆中60、40均小于70,但它们并没有70靠近根结点)
如果按照层序遍历的方式给结点从1开始编号,则结点之间满足如下关系:

这里为什么i要小于等于⌊n/2⌋呢?相信大家可能都忘记了二叉树的性质5(详见本书6.6节),其实忘记也不奇怪,这个性质在我们讲完之后,就再也没有提到过它。可以说,这个性质仿佛就是在为堆准备的。性质5的第一条就说一棵完全二叉树,如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲是结点⌊i/2⌋。那么对于有n个结点的二叉树而言,它的i值自然就是小于等于⌊n/2⌋了。性质5的第二、三条,也是在说明下标i与2i和2i+1的双亲子女关系。如果完全忘记的同学不妨去复习一下。
如果将图9-7-2的大顶堆和小顶堆用层序遍历存入数组,则一定满足上面的关系表达。如图9-7-3。
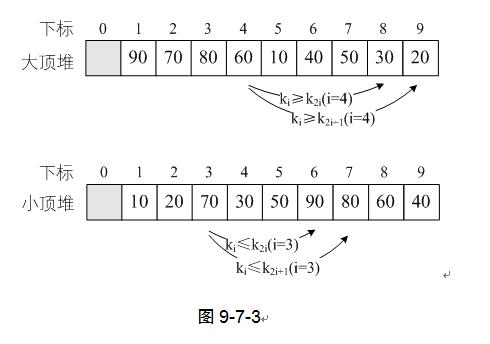
我们现在讲这个堆结构,其目的就是为了堆排序用的。
我们前面讲到简单选择排序,它在待排序的n个记录中选择一个最小的记录需要比较n-1次。本来这也可以理解,查找第一个数据需要比较这么多次正常的,否则如何知道它是最小的记录。
可惜的是,这样的操作并没有把每一趟的比较结果保存下来,在后一趟的比较中,有许多比较在前一趟已经做过了,但由于前一趟排序时未保存这些比较结果,所以后一趟排序时又重复执行了这些比较操作,因而记录的比较次数较多。
如果可以做到每次在选择到最小的记录的同时,并根据比较对其他记录做出相应的调整,那样排序的总体效率就会非常高了。而堆排序(Heap Sort),就是对简单选择排序进行的一种改进,这种改进的效果是非常明显的。堆排序算法是Floyd和Williams在1964年共同发明的,同时,他们发明了堆这样的数据结构。
回忆一下我们小时候,特别是男同学,基本都玩过叠罗汉的恶作剧。通常都是先把某个要整的人按倒在地,然后大家就一拥而上扑了上去……后果?后果当然就是一笑了知,一个恶作剧而已。不过在西班牙的加泰罗尼亚地区,他们将叠罗汉视为了正儿八经的民族体育活动,如图9-7-1,可以想像当时场面的壮观。

叠罗汉运动是把人堆在一起,而我们这里要介绍的“堆”结构相当于把数字符号堆成一个塔型的结构。当然,这绝不是简单的堆砌。大家看图9-7-2,能够找到什么规律吗?

很明显,我们可以发现它们都是二叉树,如果观察仔细些,还能看出它们都是完全二叉树。左图中根结点是所有元素中最大的,右图的根结点是所有元素中最小的。再细看看,发现左图每个结点都比它的左右孩子要大,右图每个结点都比它的左右孩子要小。这就是我们要讲的堆结构。
堆是具有下列性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆(例如图9-7-2左图);或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆(例如图9-7-2右图)。
这里需要注意从堆的定义可知,根结点一定是堆中所有结点最大(小)者。较大(小)的结点靠近根结点(但也不绝对,比如右图小顶堆中60、40均小于70,但它们并没有70靠近根结点)
如果按照层序遍历的方式给结点从1开始编号,则结点之间满足如下关系:

这里为什么i要小于等于⌊n/2⌋呢?相信大家可能都忘记了二叉树的性质5(详见本书6.6节),其实忘记也不奇怪,这个性质在我们讲完之后,就再也没有提到过它。可以说,这个性质仿佛就是在为堆准备的。性质5的第一条就说一棵完全二叉树,如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲是结点⌊i/2⌋。那么对于有n个结点的二叉树而言,它的i值自然就是小于等于⌊n/2⌋了。性质5的第二、三条,也是在说明下标i与2i和2i+1的双亲子女关系。如果完全忘记的同学不妨去复习一下。
如果将图9-7-2的大顶堆和小顶堆用层序遍历存入数组,则一定满足上面的关系表达。如图9-7-3。

我们现在讲这个堆结构,其目的就是为了堆排序用的。


