《大话数据结构》第9章 排序 9.4 简单选择排序
9.4.1 简单选择排序算法
爱炒股票短线的人,总是喜欢不断的买进卖出,想通过价差来实现盈利。但通常这种频繁操作的人,即使失误不多,也会因为操作的手续费和印花税过高而获利很少。还有一种做股票的人,他们很少出手,只是在不断的观察和判断,等到时机一到,果断买进或卖出。他们因为冷静和沉着,以及交易的次数少,而最终收益颇丰。
冒泡排序的思想就是不断的在交换,通过交换完成最终的排序,这和做股票短线频繁操作的人是类似的。我们可不可以像只有在时机非常明确到来时才出手的股票高手一样,也就是在排序时找到合适的关键字再做交换,并且只移动一次就完成相应关键字的排序定位工作呢?这就是选择排序法的初步思想。
选择排序的基本思想是每一趟在n-i+1(i=1,2,…,n-1)个记录中选取关键字最小的记录作为有序序列的第i个记录。我们这里先介绍的是简单选择排序法。
简单选择排序法(Simple Selection Sort)就是通过n-i次关键字间的比较,从n-i+1个记录中选出关键字最小的记录,并和第i(1≤i≤n)个记录交换之。
我们来看代码。
/* 对顺序表L作简单选择排序 */
void SelectSort(SqList *L)
{
int i,j,min;
for(i=1;i<L->length;i++)
{
min = i; /* 将当前下标定义为最小值下标 */
for (j = i+1;j<=L->length;j++) /* 循环之后的数据 */
{
if (L->r[min]>L->r[j]) /* 如果有小于当前最小值的关键字 */
min = j; /* 将此关键字的下标赋值给min */
}
if(i!=min) /* 若min不等于i,说明找到最小值,交换 */
swap(L,i,min); /* 交换L->r[i]与L->r[min]的值 */
}
}
代码应该说不难理解,针对待排序的关键字序列是{9,1,5,8,3,7,4,6,2},对i从1循环到8。当i=1时,L.r[i]=9,min开始是1,然后与j=2到9比较L.r[min]与L.r[j]的大小,因为j=2时最小,所以min=2。最终交换了L.r[2]与L.r[1]的值。如图9-4-2,注意,这里比较了8次,却只交换数据操作一次。
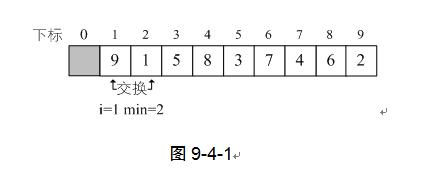
当i=2时,L.r[i]=9,min开始是2,经过比较后,min=9,交换L.r[min]与L.r[i]的值。如图9-4-3,这样就找到了第二位置的关键字。
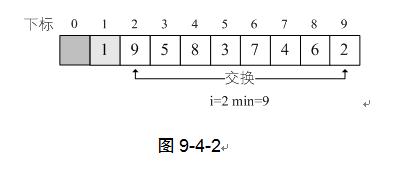
当i=3时,L.r[i]=5,min开始是3,经过比较后,min=5,交换L.r[min]与L.r[i]的值。如图9-4-4。
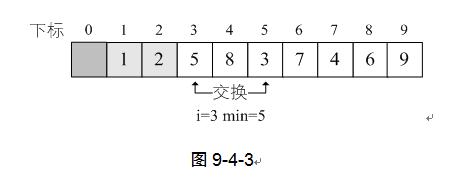
之后的数据比较和交换完全雷同,最多经过8次交换,就可完成排序工作。
9.4.2 简单选择排序复杂度分析
从简单选择排序的过程来看,它最大的特点就是交换移动数据次数相当少,这样也就节约了相应的时间。分析它的时间复杂度发现,无论最好最差的情况,其比较次数都是一样的多,第i趟排序需要进行ni次关键字的比较,此时需要比较 次。而对于交换次数而言,当最好的时候,交换为0次,最差的时候,也就初始降序时,交换次数为n-1次,基于最终的排序时间是比较与交换的次数总和,因此,总的时间复杂度依然为O(n2)。
应该说,尽管与冒泡排序同为O(n2),但简单选择排序的性能上还是要略优于冒泡排序。


