实验三 朴素贝叶斯算法及应用

实验三 朴素贝叶斯算法及应用

作业信息

博客班级	https://edu.cnblogs.com/campus/ahgc/machinelearning
作业要求	https://edu.cnblogs.com/campus/ahgc/machinelearning/homework/12085
作业目标	理解朴素贝叶斯算法原理，掌握其实现方法并解决实际问题
学号	<3180701337>

一、实验目的

1.理解朴素贝叶斯算法原理，掌握朴素贝叶斯算法框架；

2.掌握常见的高斯模型，多项式模型和伯努利模型；

3.能根据不同的数据类型，选择不同的概率模型实现朴素贝叶斯算法；

4.针对特定应用场景及数据，能应用朴素贝叶斯解决实际问题。

二、实验内容

1.实现高斯朴素贝叶斯算法。

2.熟悉sklearn库中的朴素贝叶斯算法；

3.针对iris数据集，应用sklearn的朴素贝叶斯算法进行类别预测。

4.针对iris数据集，利用自编朴素贝叶斯算法进行类别预测。

三、实验报告要求

1.对照实验内容，撰写实验过程、算法及测试结果；

2.代码规范化：命名规则、注释；

3.分析核心算法的复杂度；

4.查阅文献，讨论各种朴素贝叶斯算法的应用场景；

5.讨论朴素贝叶斯算法的优缺点。

四、代码实现及注释

1.代码注释

（1）朴素贝叶斯

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt #导入各类工具包和绘图库
%matplotlib inline

from sklearn.datasets import load_iris 
from sklearn.model_selection import train_test_split #将原始数据划分为数据集与测试集两个部分

from collections import Counter #计数器
import math #导入math函数

（2）

# data
def create_data(): 
    iris = load_iris() #加载数据集(这里使用的是鸢尾花数据集)
    df = pd.DataFrame(iris.data, columns=iris.feature_names) #转化为DataFrame
    df['label'] = iris.target #增加一列为类别标签
    df.columns = [
        'sepal length', 'sepal width', 'petal length', 'petal width', 'label'
    ]  #定义表中每一列
    data = np.array(df.iloc[:100, :]) #df.iloc[x,y]中x为数据的行索引，y为数据的列索引
    # print(data)
    return data[:, :-1], data[:, -1]

（3）

X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

（4）

X_test[0], y_test[0]

(array([4.9, 3.6, 1.4, 0.1]), 0.0)

（5）GaussianNB 高斯朴素贝叶斯

class NaiveBayes:
    def __init__(self):
        self.model = None
        
    # 数学期望
    @staticmethod
    def mean(X):
        return sum(X) / float(len(X))
    
    # 标准差（方差）
    def stdev(self, X):
        avg = self.mean(X)
        return math.sqrt(sum([pow(x - avg, 2) for x in X]) / float(len(X)))
    
    # 概率密度函数
    def gaussian_probability(self, x, mean, stdev):
        exponent = math.exp(-(math.pow(x - mean, 2) /
                              (2 * math.pow(stdev, 2))))
        return (1 / (math.sqrt(2 * math.pi) * stdev)) * exponent
    
    # 处理X_train
    def summarize(self, train_data):
        summaries = [(self.mean(i), self.stdev(i)) for i in zip(*train_data)]
        return summaries
    
    # 分类别求出数学期望和标准差
    def fit(self, X, y):
        labels = list(set(y))
        data = {label: [] for label in labels}
        for f, label in zip(X, y):
            data[label].append(f)
        self.model = {
            label: self.summarize(value)
            for label, value in data.items()
        }
        return 'gaussianNB train done!'
        
    # 计算概率
    def calculate_probabilities(self, input_data):
        # summaries:{0.0: [(5.0, 0.37),(3.42, 0.40)], 1.0: [(5.8, 0.449),(2.7, 0.27)]}
        # input_data:[1.1, 2.2]
        probabilities = {}
        for label, value in self.model.items():
            probabilities[label] = 1
            for i in range(len(value)):
                mean, stdev = value[i]
                probabilities[label] *= self.gaussian_probability(
                    input_data[i], mean, stdev)
        return probabilities
            
    # 类别
    def predict(self, X_test):
        # {0.0: 2.9680340789325763e-27, 1.0: 3.5749783019849535e-26}
        label = sorted(
            self.calculate_probabilities(X_test).items(),
            key=lambda x: x[-1])[-1][0]
        return label
    
    def score(self, X_test, y_test):
        right = 0
        for X, y in zip(X_test, y_test):
            label = self.predict(X)
            if label == y:
                right += 1
        
        return right / float(len(X_test))

（6）

model = NaiveBayes()

（7）

model.fit(X_train, y_train)

'gaussianNB train done!'

（8）

print(model.predict([4.4, 3.2, 1.3, 0.2])) #输出模型预测数据

0.0

（9）

model.score(X_test, y_test)

1.0

（10）scikit-learn实例

from sklearn.naive_bayes import GaussianNB

（11）

clf = GaussianNB()
clf.fit(X_train, y_train)

（12）

clf.score(X_test, y_test)

1.0

（13）

clf.predict([[4.4, 3.2, 1.3, 0.2]])

array([0.])

（14）

from sklearn.naive_bayes import BernoulliNB, MultinomialNB # 伯努利模型和多项式模型

2.运行结果

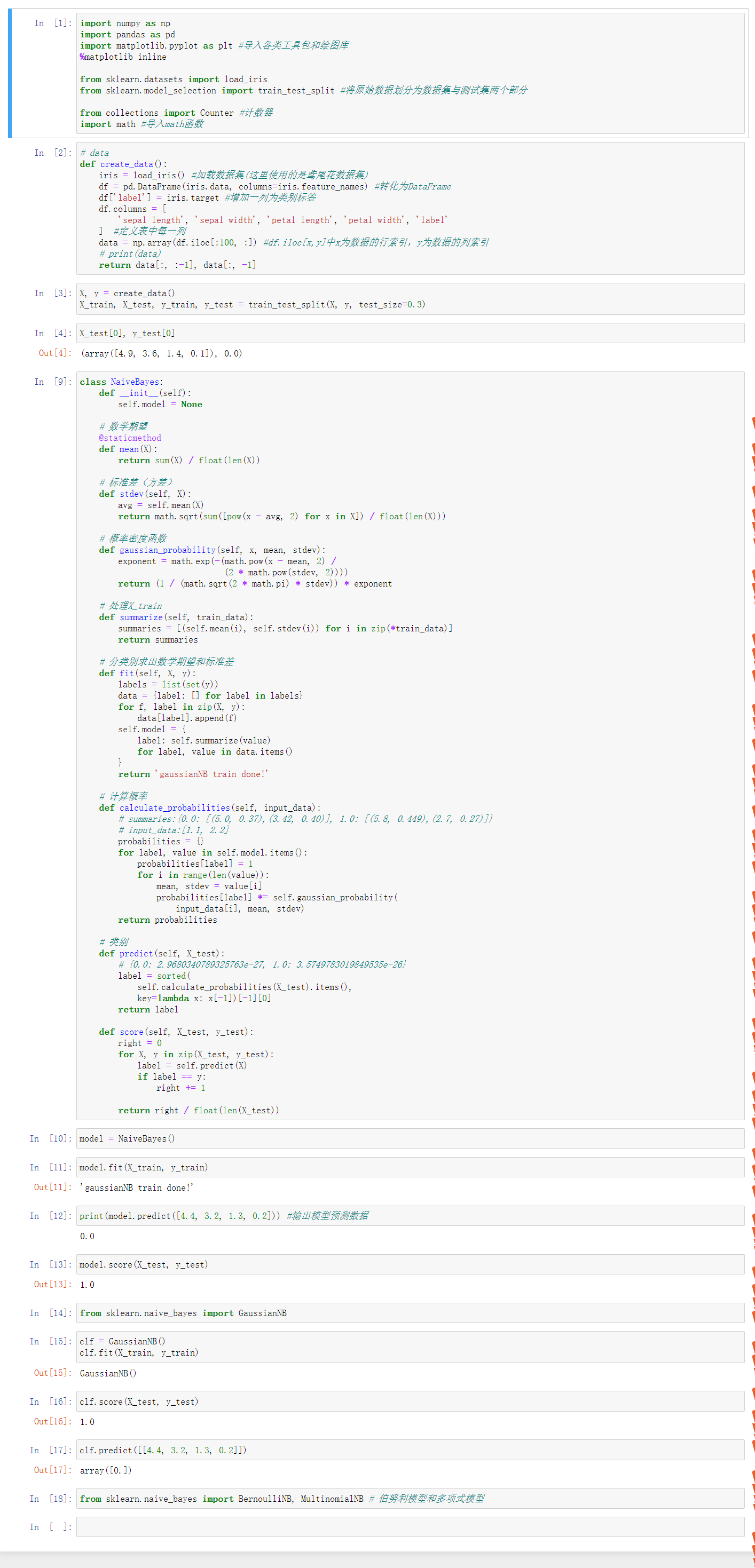
3.各种朴素贝叶斯算法的应用场景

高斯朴素贝叶斯:适用于特征是高斯分布的，对人的身高体重，物体的长度等这些连续性的变量进行分类。
多项式朴素贝叶斯:适用于特征是多项式分布的，常用于离散值模型里。例如文本分类问题，统计某文档中出现的单词，允许重复之类的问题。
伯努利朴素贝叶斯:适用于特征是二项分布的，每个特征的取值是布尔型的，即true和false，或者1和0。例如在文本分类中判断某一特征是否出现。

4.朴素贝叶斯算法的优缺点

算法优点：
（1）朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
（2）对小规模的数据表现很好，能个处理多分类任务，适合增量式训练。
（3）对缺失数据不太敏感，算法也比较简单，常用于文本分类。
算法缺点：
（1）理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
（2）需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
（3）由于是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。
（4）对输入数据的表达形式很敏感。

五、实验小结

通过本次实验，我对朴素贝叶斯算法的原理有了一定的了解，也掌握其相关的应用方法和应用场景。朴素贝叶斯方法是在贝叶斯算法的基础上进行了相应的简化，即假定给定目标值时属性之间相互条件独立。也就是说没有哪个属性变量对于决策结果来说占有着较大的比重，也没有哪个属性变量对于决策结果占有着较小的比重，这也就是其中朴素二字的由来，虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果，但是在实际的应用场景中，极大地简化了贝叶斯方法的复杂性。朴素贝叶斯原理简单但在一些分类问题中应用广泛，值得我们深入地学习。