循环结构练习题

循环结构练习链接

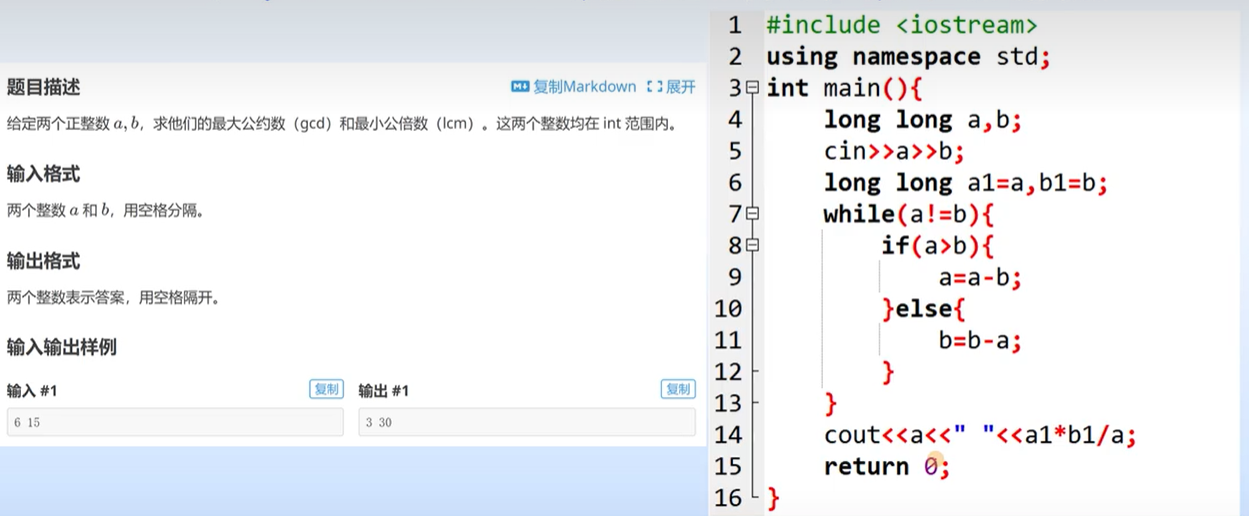
1、辗转相除法求两数的最大公约数

问题：尼克有一根长15米的铁丝，格莱尔有一根长18米的铁丝，要把它们截成同样长的小段，不许剩余，每段最长有几米？试编一程序，求出每段最长的米数。
  这是求最大公约数的问题。两根铁丝的长度分别用m和n表示，采用辗转相除法求最大公约数。辗转相除法求最大公约数的数学原理

其思路是：
(1)求m除以n的余数r。
(2)当r==0时，则n为最大公约数，输出n并结束程序；当r!=0,执行(3)。
(3)将n的值赋给m,将r的值赋给n;再求m除以n的余数r。
(4)转到第2步。

测试数据

‌输入数据‌：49 14
‌输出数据‌：7

‌输入数据‌：36 18
‌输出数据‌：6

‌输入数据‌：55 20
‌输出数据‌：5

‌输入数据‌：100 25
‌输出数据‌：25

‌输入数据‌：120 48     112 64
‌输出数据‌：24

扩展：求最大约数与最小倍数练习


网上OJ相关练习与提交

2、斐波那契数列

（1）母题————斐波那契数列指的是这样一个数列：1,1,2,3,5,8,13,21，··，这个数列从第3个数开始,每个数都等于前面两个数的和。这个数列与大自然中植物的关系极为密切，几乎所有花朵的花瓣数都来自这个数列中的一项数字，同时在植物的叶、枝、茎等排列中也存在斐波那契数列。

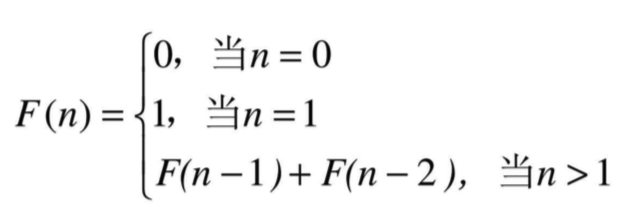
  试编一程序,输出斐波那契数列中的前n项。

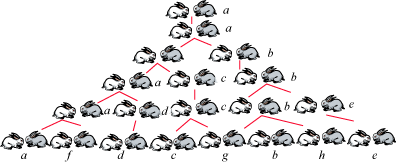
（2）兔子繁殖的问题(参考视频）
  有一对兔子，从出生后第3个月起每个月都生一对兔子（总是一雄一雌），小兔子长到第三个月后每个月又生一对兔子，假如兔子都不死，问兔子每个月的总对数。（输出20个月的数量）

        
OJ相关题目
大自然里的斐波那契数列

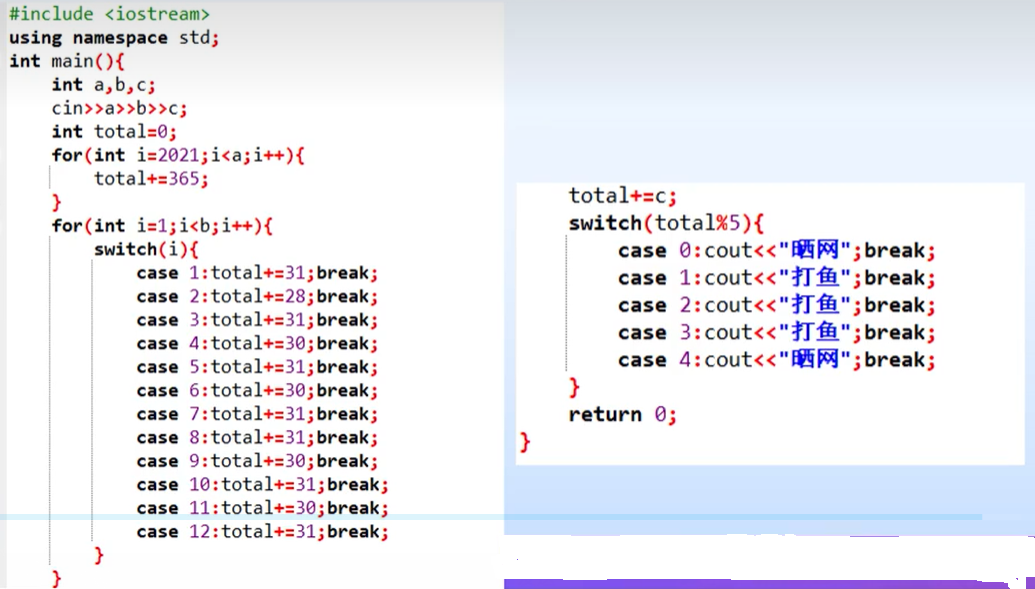
3、渔夫打鱼晒网问题

  如果一个渔夫从 2011 年 1 月 1 日开始每三天打一次渔，两天晒一次网，编程实现当输入 2011 1 月 1 日以后的任意一天，输出该渔夫是在打渔还是在晒网。
  本题主要有以下两个思路要点：
  (1) 判断输入的年份（2011 年以后包括 2011 年）是否为闰年。该函数的核心内容就是闰年的判断条件即能被 4 整除但不能被 100 整除，或能被 400 整除。
  (2) 求输入日期距 2011 年 1 月 1 日有多少天。首先判断 2011 年距输入的年份有多少年，这其中有多少年是闰年就将 sum 加多少个 366，有多少年是平年便将 sum 加上多少个 365。
其次要将 12 个月每月的天数存到数组中，因为闰年 2 月份的天数有别于平年，故采用两个数组 a 和 b 分别存储。若输入年份是平年，月份为 m 时就在前面累加日期的基础上继续累加存储着平年每月天数的数组的前 m-1 个元素，将累加结果加上输入的日期便求出了最终结果。闰年的算法类似。

4、数字分割和翻转

（1）母题————数字分割和翻转



（2）回文数
  问题：“地满红花红满地，天连碧水碧连天”是一副回文联，用回文形式写成的对联，既可以顺读，也可以倒读，意思不变。在数学中也存在这样特征的一类数，称为回文数。设n是一任意自然数，将n各个数位上的数字反向排列所得自然数m,若m等于n,则n为回文数。例如，1234321是回文数，1234567不是回文数。

试编一程序,判断一个自然数是不是回文数。

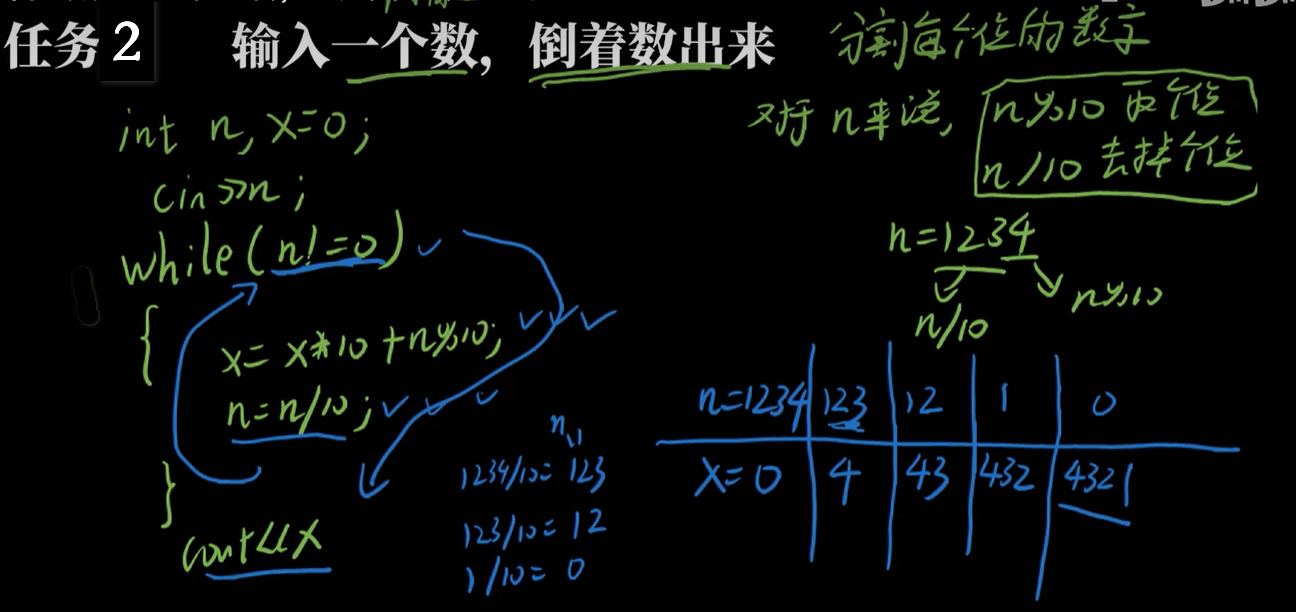
  如何将自然数n各个数位上的数字反向排列，组成新的自然数m?如输入的数n为123时，可先将m的初值设为0。第1次，先运用整除求余运算将n个位上的数字分离出来，即123%10得到3，再用m*10+3组成的新数赋值给m,然后将n的值缩小10倍；第2次，重复上面的步骤后，m为32,n为1；第3次，重复上面的步骤后，m为321，n为0。由于此时n的值为0，新数m构造完成，如图所示。

  因为输入的自然数其位数是不确定的，因此每次分离数位时，循环次数也是不确定的。for语句使用很灵活，不仅可以用于循环次数已经确定的情况，而且也可以用于循环次数不确定而循环结束条件确定的情况。
流程图：

可以把for语句在形式上稍作修改,程序如下:
for(n=num; n>0; n=n/10)m=m*10+n%10;

母题概念的解析
  母题在教育学中指的是各门学科包含若干知识点的基本题、典型题，也是中高考命题所参照的原型题​。掌握母题是一种快速、扎实的掌握学科知识的方法，有助于统一整个作品，形成有意义线索，是高考、中考总复习的最佳捷径。
  母题在数学领域中，指的是那些反复出现、具有典型性和普遍性，能够涵盖大量知识点、解题方法和数学思想的基本问题。以下是对数学母题的详细解释：
一、定义与特点
‌定义‌：数学母题是构成数学知识体系的核心，是理解和掌握数学概念、原理的关键。
‌特点‌：反复出现，在数学学习中，母题会不断出现，帮助学生巩固和深化对数学知识的理解。
典型性和普遍性：母题具有代表性，能够体现数学学科的基本特点和规律。
涵盖知识点广泛：母题往往涉及多个知识点，通过解决母题，学生可以掌握更多的数学知识。
二、作用与意义
‌构建知识体系‌：数学母题是数学知识体系的基础，通过母题的学习，学生可以建立起扎实的数学基础。
‌提高解题能力‌：通过解决母题，学生可以锻炼数学思维，提高解题能力，培养解决实际问题的能力。
‌深化数学理解‌：母题往往包含深刻的数学思想和方法，通过深入研究母题，学生可以深化对数学概念和原理的理解。
‌促进创新思维‌：母题往往具有启发性和开放性，通过对母题的研究和探索，学生可以激发创新思维，培养创新意识。
三、实例分析
‌几何学中的母题‌：如“勾股定理”和“圆的性质”，这些母题在几何学中具有广泛的应用，是解决相关问题的关键。
‌代数学中的母题‌：如“多项式”和“方程”，这些母题是代数学的基础，通过解决这些母题，学生可以掌握代数学的基本概念和解题方法。
‌微积分中的母题‌：如“导数”和“积分”，这些母题是微积分学的核心，通过学习和解决这些母题，学生可以深入理解微积分的基本原理和应用。
  综上所述，数学母题是数学学习中的基础和关键，掌握母题是提高数学素养和能力的必经之路。因此，在数学学习中，学生应重视母题的学习和研究，通过不断练习和深入思考，掌握更多的数学知识和解题方法。
        返回

渔夫打鱼晒网问题解题参考

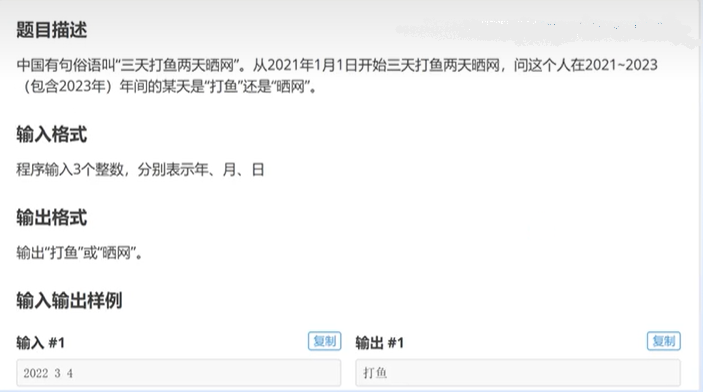
这题时段短且明确不用考虑闰年，程序较简单：