多项式乘法

本篇是因为学不会用蝴蝶变换优化所致。咱就是说，为什么一个常数优化会成为学习 FFT 的瓶颈呢？

基本思想

基本思想就是把系数相乘转化为点值相乘。

首先，根据代数基本原理，对于一个 \(n\) 次多项式 \(f(x)=a_0+a_{1}x+a_{2}x^2+\dots +a_{n}x^n\)，如果知道 \(n+1\) 组 \(f(x_i)=y_i\)，一定可以确定该多项式的值。代码实现中，至少可以通过拉格朗日插值法 \(O(n^2)\) 求出：

\[f(x)=\sum_{i=1}^{n+1}y_i\prod_{i\ne j} \frac{x-x_j}{x_i-x_j} \]

所以我们能 \(O(n^2)\) 的将多项式的 \(n+1\) 个系数和 \(n+1\) 个点值相互转化。

而对于 \(H(x)=F(x)G(x)\)，有 \(H(x_i)=F(x_i)G(x_i)\)，也就是说多项式的乘法在系数表示法下是 \(O(n)\) 的。

于是我们的思路就是：将多项式转化为系数表示；在系数表示下相乘；把答案的系数表示转化回点值。

FFT

怎样快速进行系数和点值的转化呢？

傅里叶变换告诉我们代入单位复根：\(n\) 次单位复根 \(\omega_n\) 可以理解为复平面上的单位圆圆上面从 \(x\) 轴正半轴开始的第一个 \(n\) 等分点。

根据三角函数的两角和公式，\((\cos x,i\sin x)\) 和 \((\cos y,i\sin y)\) 相乘得到结果 \((\cos x\cos y-\sin x\sin y,i(\cos x\sin y+\sin x\cos y))\) 就是 \((\cos(x+y),i\sin(x+y))\)，所以两个单位圆上的点相乘，就是它们的辐角相加。辐角就是说这个点和原点连线与 \(x\) 轴正半轴的夹角。

所以有 \(w_n^n=1\)，相当于转一圈嘛。

那么，怎么求 \(\omega_n\) 呢？其实它的辐角就是 \(\frac{2\pi}{n}\) 嘛，所以是 \(\omega_n=(cos\frac{2\pi}{n},sin\frac{2\pi}{n})\)。

对于多项式 \(f(x)=a_0+a_{1}x+a_{2}x^2+\dots +a_{n}x^n\)，我们试着把点值 \(w_{n+1}^0,w_{n+1}^1,\dots,2_{n+1}^n\) 代入。

注意次数为 \(n\) 的多项式长度为 \(n+1\)。

然后再用快速幂的方式把多项式分裂：（不妨假设多项式的长度 \(n+1\) 是偶数）

\[f0(x)=a_0+a_{2}x+a_{4}x^2+a_{6}x^3+\dots +a_{n-1} x^{\frac{n-1}{2}} \]

\[f1(x)=a_1+a_{3}x+a_{5}x^2+a_{7}x^3+\dots +a_{n} x^{\frac{n-1}{2}} \]

这样有 \(f(x_i)=f0(x_i^2)+x_i f1(x_i^2)\)。

这样，比如说我们需要 \(f(\omega_{n+1}^i)=f0(\omega_{n+1}^{2i})+\omega_{n+1}^i f1(\omega_{n+1}^{2i})=f0(\omega_{\frac{n+1}{2}}^{i})+\omega_{n+1}^i f1(\omega_{\frac{n+1}{2}}^{i})\)，也就是说我们只需要 \(f0\) 和 \(f1\) 在 \(\omega_{\frac{n+1}{2}}^0,\omega_{\frac{n+1}{2}}^1,\omega_{\frac{n+1}{2}}^2,\dots,\omega_{\frac{n+1}{2}}^{\frac{n-1}{2}}\) 的点值。

为什么会有 \(\omega_{\frac{n+1}{2}}^{\frac{n-1}{2}}\) 这个上界呢？对于 \(i=\frac{n+1}{2}+k\) 式子，有

\[f(\omega_n^i)=f0(\omega_{\frac{n+1}{2}}^{i})+\omega_{n+1}^i f1(\omega_{\frac{n+1}{2}}^{i})=f0(\omega_{\frac{n+1}{2}}^{k})+\omega_{n+1}^i f1(\omega_{\frac{n+1}{2}}^{k})=f0(\omega_{\frac{n+1}{2}}^{k})-\omega_{n+1}^k f1(\omega_{\frac{n+1}{2}}^{k}) \]

并且有 \(k\le \frac{n-1}{2}\)，所以分 \(i<\frac{n+1}{2}\) 和 \(i\ge\frac{n+1}{2}\) 两种情况讨论即可。

这样转化为了两个长度为 \(\frac{n+1}{2}\) 的子问题，由于问题总规模没变，可以递归。

递归的终点是长度 \(n=1\) 为 \(1\) 的情况，此时多项式只有常数项，故点值等于系数。

一个小问题：并不需要讨论 \(n+1\) 是奇数的情况，递归前，先把多项式长度补充到 2 的整次幂可以保证每次 \(n+1\) 都是偶数。

写一下代码，大概是这样：

#include<bits/stdc++.h>
using namespace std;
const double phi=acos(-1);
struct xs
{
    double x,y;
    friend xs operator +(xs x,xs y){x.x+=y.x;x.y+=y.y;return x;}
    friend xs operator -(xs x,xs y){x.x-=y.x;x.y-=y.y;return x;}
    friend xs operator *(xs x,xs y)
    {return (xs){x.x*y.x-x.y*y.y,x.y*y.x+x.x*y.y};}
    void print(){printf("%.5lf %.5lf\n",x,y);}
}w[2100005];
void FFT(vector<xs>&x,int len)
{//这里的 len 是多项式长度，也就是 n+1
	if(len==1) return;
	vector<xs>l,r;
	l.resize(len/2);r.resize(len/2);
	for(int i=0;i+1<len;i+=2) l[i/2]=x[i],r[i/2]=x[i+1];
	FFT(l,len/2);
	FFT(r,len/2);
    xs wn=(xs){cos(phi*2/len),sin(phi*2/len)};
	for(int i=1;i<len/2;i++) w[i]=w[i-1]*wn;
	for(int i=0;i<len/2;i++)
	{
		xs tmp=r[i]*w[i];
		x[i]=l[i]+tmp;
		x[i+len/2]=l[i]-tmp;
	}
    //这里 x 数组相当于返回值，传入原来的系数数组，返回得到的点值数组
}

IFFT

以上是系数转点值的操作，那么求出答案的点值后表示怎么回归系数表示呢？

可能涉及到一些矩阵、同余有关的知识）

首先如果把系数表示法转化为点值表示法的过程写成矩阵乘法，那大概是这样（以下 \(n\) 就是多项式长度而不是次数）：

\[\begin{bmatrix} \omega_n^0&\omega_n^0&\omega_n^0&\dots&\omega_n^0\\ \omega_n^0&\omega_n^1&\omega_n^2&\dots&\omega_n^{n-1}\\ \vdots&&\ddots&&\vdots\\ \omega_n^0&\omega_n^{n-1}&\omega_n^{n*(n-1)}&\dots&\omega_n^{(n-1)*(n-1)} \end{bmatrix} \begin{bmatrix} a_0\\a_1\\\vdots\\a_{n-1} \end{bmatrix} \]

我们称前一个方阵为 \(A\)，多项式构成的竖矩阵称作 \(F\)，那么我们得到了答案的点值表达 \(AF\)，而只要算出 \(A^{-1}(AF)=F\) 就可以求出系数表达。

那么要知道 \(A\) 的逆，设其为 \(B\)，则需要满足对于第 \(y\) 列：

\[\begin{cases} \sum_{i=0}^{n-1} \omega_n^{ix}a_i=1&(x=y)\\ \sum_{i=0}^{n-1} \omega_n^{ix}a_i=0&(x\neq y) \end{cases}\]

结论是如果令 \(b_{i,j}=\frac{\omega_n^{-ix}}{n}\) 就对了。

首先第一行的式子显然成立，因为这里 \(a_i=b_{y,i}=\frac{\omega_n^{-iy}}{n}=\frac{\omega_n^{-ix}}{n}\)。

然后第二行就相当于 \(\sum \frac{\omega_n^{ix-iy}}{n}=\sum \frac{\omega_n^{i*(x-y)}}{n}\)，所以只需要证明 \(\sum_{i=0}^{n-1} \omega_n^{i*t}=0\)。

因为 \(\omega_n^{ni}=1\)，所以相当于是 \(\omega_n^{it\mod n}\)。而由于 \(it\mod n\) 这种东西循环节一定是 \(n\) 的因数，所以这个求和一定是若干整循环节。而由于循环是从 \(1\) 开始的，每一个长度为 \(x\) 的循环节就相当于单位圆的 \(x\) 等分点，故而每个循环节的和都是 \(0\)（甚至可以考虑合力为 \(0\)），所以上式成立。

然后我们发现只要把单位复根取一下负一次方，再把结果除上 \(n\)，IFFT 的过程和 FFT 是一样的。

也就是说把刚才那个函数改一下就行：

#include<bits/stdc++.h>
using namespace std;
const double phi=acos(-1);
int len=1,l;
struct xs
{
    double x,y;
    friend xs operator +(xs x,xs y){x.x+=y.x;x.y+=y.y;return x;}
    friend xs operator -(xs x,xs y){x.x-=y.x;x.y-=y.y;return x;}
    friend xs operator *(xs x,xs y)
    {return (xs){x.x*y.x-x.y*y.y,x.y*y.x+x.x*y.y};}
    void print(){printf("%.5lf %.5lf\n",x,y);}
}w[2100005];
vector<xs>a,b,c;
void FFT(vector<xs>&x,int len,int op)
{
	if(len==1) return;
	vector<xs>l,r;
	l.resize(len/2);r.resize(len/2);
	for(int i=0;i+1<len;i+=2) l[i/2]=x[i],r[i/2]=x[i+1];
	FFT(l,len/2,op);
	FFT(r,len/2,op);
    xs wn=(xs){cos(phi*2/len),op*sin(phi*2/len)};
    //op=-1 就是 IFFT，把虚数轴坐标取相反数就是取 -1 次方
	for(int i=1;i<len/2;i++) w[i]=w[i-1]*wn;
	for(int i=0;i<len/2;i++)
	{
		xs tmp=r[i]*w[i];
		x[i]=l[i]+tmp;
		x[i+len/2]=l[i]-tmp;
	}
}
int main()
{
    int n,m,xx;cin>>n>>m;w[0]=(xs){1,0};
    while(len<n+m+1) len*=2,l++;
	a.resize(len);b.resize(len);c.resize(len);
    for(int i=0;i<=n;i++) scanf("%d",&xx),a[i]=(xs){1.0*xx,0};
    for(int i=0;i<=m;i++) scanf("%d",&xx),b[i]=(xs){1.0*xx,0};
    FFT(a,len,1);
	FFT(b,len,1);
    for(int i=0;i<len;i++)
    c[i]=a[i]*b[i];
    FFT(c,len,-1);
    for(int i=0;i<len;i++)
    c[i].x/=len;//别忘了除掉 n
    for(int i=0;i<=n+m;i++)
    printf("%d ",(int)(c[i].x+0.5));
    return 0;
}

使用上面的代码实现 FFT 和 IFFT，在洛谷模板题所有测试点总共运行了 3.14s。

卡常之一

首先要优化掉递归的时间。

比如 \(len=8\) 的情况，相当于你传入的数组下标从 0 1 2 3 4 5 6 7 到 0 2 4 6 和 1 3 5 7，再到 0 4,2,6,1 5,3,7。

我们注意到这样递归相当于每层把全部 \(len\) 个数分成若干数组传进去，进行运算后总共返回 \(len\) 个值。那不妨把返回值存放在原下标下，比如说我们处理下标 0 2 4 6 时，得到四个点值，仍然存放在数组 0 2 4 6 的位置，这样递归就相当于若干层，每一层由上一层的值得到。

举个例子，进行 0 2 4 6 这次递归时，上面的代码中进行的操作是先进行 0 4 和 2 6 两次递归，然后分别得到两个点值数组 \(l_0,l_1\) 和 \(r_0,r_1\)，而如果我们把 \(l_0,l_1\) 存放在 0 4 的下标；把 \(r_0,r_1\) 存放在 2 6 的下标，就相当于我们要根据下一层在 0 2 4 6 位置存放好的 \(l,r\) 数组，得到 0 2 4 6 这一层的答案。

具体地，要根据 \(l_0,r_0\) 得到 0,4 位置的值，根据 \(l_1,r_1\) 得到 2 6 位置的值，也就是说要用下一层 0 2 位置的值更新 0 4 位置的值；同时用 4 6 位置的值更新 2 6 位置的值。

如果我们知道这些更新进行的方式，就可以用滚动数组实现了。以下是例子：

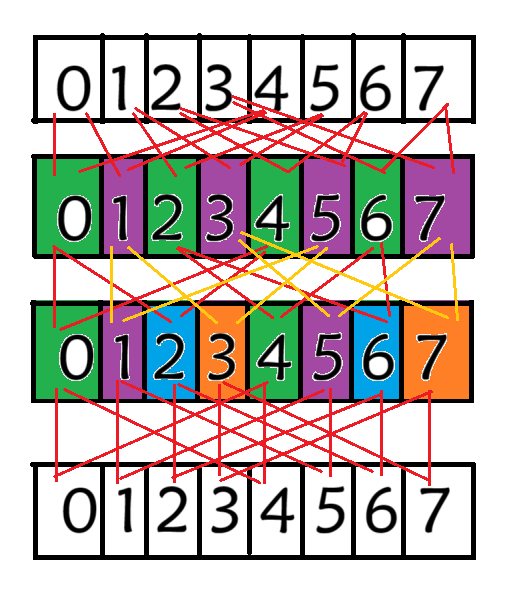
用代码实现的话，还需要找一下规律。

我们称这四层分别为 0,1,2,3 层，每一层分为若干块。这里所说的分为若干块就是递归的时候分归多个函数处理。给每个块一个编号，即它被计算的顺序，可以考虑一棵递归树的前序遍历。例如 0 4,2,6,1 5,3,7 就是第二层按顺序的第一到第四块。

那么我们发现一直是 \(i+1\) 层的一对数 \(x<y\) 更新 \(i\) 层的另一对数 \(p<q\)。而且由于每一块都是公差相等的等差数列，故而 \(x\) 在 \(i+1\) 层所属块的第一个下标就是 \(p,q\) 在 \(i\) 层所属块的第一个下标。并且根据更新规则，\(x\) 在块中的排位就是 \(p\) 在块中的排位。然后怎么求 \(x\) 所属块的第一个下标呢？可以看出是 x&((1<<i)-1)。怎么求 \(x\) 在块中的排位呢？可以看出等差数列的公差是 \(2^i\)。

并且由于每次分块都是按二进制下第 \(i\) 位分组，所以 \(x,y\) 一定一个该位为 \(1\)，另一个该位为 \(0\)。所以只需要枚举所有该位为 \(0\) 的数为 \(x\) 即可。

嘛，这种规律真的挺容易绕晕的，不过只要认真找不愁看不出规律）））

总之，可以写出以下代码：

#include<bits/stdc++.h>
using namespace std;
const double phi=acos(-1);
int len=1,l;
struct xs
{
    double x,y;
    friend xs operator +(xs x,xs y){x.x+=y.x;x.y+=y.y;return x;}
    friend xs operator -(xs x,xs y){x.x-=y.x;x.y-=y.y;return x;}
    friend xs operator *(xs x,xs y)
    {return (xs){x.x*y.x-x.y*y.y,x.y*y.x+x.x*y.y};}
    void print(){printf("%.5lf %.5lf\n",x,y);}
}a[2100005],b[2100005],c[2100005],w[2100005],tmp[2100005];
void FFT(xs *x,int op)
{
    for(int i=l-1;i>=0;i--)
    {
        int num=(1<<l-i-1);
        xs wn=(xs){cos(phi/num),op*sin(phi/num)};
        for(int j=1;j<num;j++) w[j]=w[j-1]*wn;
        for(int j=0;j<len;j++) tmp[j]=x[j];
        for(int j=0;j<len;j++)
        if(((j>>i)&1)==0)
        {
            int k=j+(1<<i);
            int typ=j&((1<<i)-1),pos=j>>(i+1);
            //这里 typ 是块的开头节点，pos 是块中的排位
            xs f=tmp[j],g=w[pos]*tmp[k];
            x[typ+(1<<i)*pos]=f+g;
            x[typ+(1<<i)*pos+len/2]=f-g;
        }
    }
}
int main()
{
    int n,m,xx;
    cin>>n>>m;w[0]=(xs){1,0};
    for(int i=0;i<=n;i++) scanf("%d",&xx),a[i].x=xx;
    for(int i=0;i<=m;i++) scanf("%d",&xx),b[i].x=xx;
    while(len<n+m+1) len*=2,l++;
    FFT(a,1);
	for(int i=0;i<len;i++)
	a[i].print();
	FFT(b,1);
    for(int i=0;i<len;i++)
    c[i]=a[i]*b[i];
    FFT(c,-1);
    for(int i=0;i<len;i++)
    c[i].x/=len;
    for(int i=0;i<=n+m;i++)
    printf("%d ",(int)(c[i].x+0.5));
    return 0;
}

这个运行时间是 2.46s。

卡常之二

就像 01 背包可以倒序枚举而不使用滚动数组一样，思考怎么不使用滚动数组。

因为每次都是下一层的两个数 \(x,y\) 更新上一层的两个数 \(p,q\) 嘛，可以每次只备份这两个数。这要求第 \(i+1\) 层的 \(p,q\) 和第 \(i\) 层的 \(x,y\) 储存在数组的相同下标中，换句话说就是我们得换一种排列顺醋去储存，让上面那个图当中所有更新方式都像最后一排一样是单纯交叉的。

因为是两个长度为 \(t\) 的数组 \(l,r\) 其中 \(l_i,r_i\) 去更新 \(x_i,x_{i+t}\) 所以让 \(x\) 和 \(l\) 对齐后把 \(r\) 拼在 \(l\) 后面即可。

如图所示：

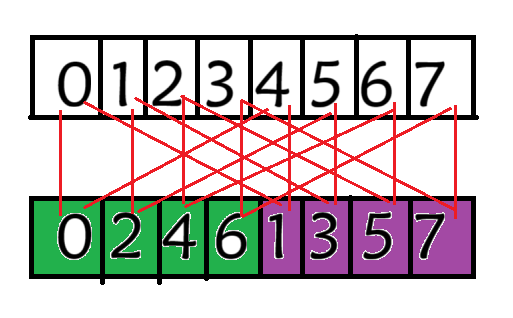
所以这样递归下去，其实就是把每层的所有块直接按编号顺序排列即可。

然后由于我们是从最后一层开始算，我们需要知道最后的排序是什么。由于从第 \(0\) 层到第 \(\log(len) -1\) 层是从二进制第 \(2^0\) 位到 \(2^{\log(len)-1}\) 位每次按照该位排序，也就相当于是把先考虑低位二进制数码，后考虑高位二进制数码的比较。换句话说，就是 \(x\) 最后的位置会是 \(x\) 二进制数码倒过来的位置。

这个用位运算就比较好实现。

可以写出如下代码（以下写最简短的，通常被背诵的版本）：

#include<bits/stdc++.h>
using namespace std;
const double phi=acos(-1);
struct xs
{
	double x,y;
    friend xs operator +(xs x,xs y){x.x+=y.x;x.y+=y.y;return x;}
    friend xs operator -(xs x,xs y){x.x-=y.x;x.y-=y.y;return x;}
    friend xs operator *(xs x,xs y)
    {return (xs){x.x*y.x-x.y*y.y,x.y*y.x+x.x*y.y};}
    void print(){printf("%.5lf %.5lf\n",x,y);}
}a[2100000],b[2100000],c[2100000];
int len=1,l,r[2100000];
void FFT(xs *x,int op)
{
	for(int i=0;i<len;i++) if(i<r[i]) swap(x[i],x[r[i]]);
	for(int i=1;i<len;i*=2)
	{
		xs wn={cos(phi/i),op*sin(phi/i)};
		for(int j=0;j<len;j+=(i*2))
		{
			xs w={1,0};
			for(int k=0;k<i;k++)
			{
				xs g=x[j+k],h=w*x[i+j+k];
				x[j+k]=g+h;
				x[i+j+k]=g-h;
				w=w*wn;
			}
		}
	}
}
int main()
{
	int n,m,xx;cin>>n>>m;
    for(int i=0;i<=n;i++) scanf("%d",&xx),a[i].x=xx;
    for(int i=0;i<=m;i++) scanf("%d",&xx),b[i].x=xx;
    while(len<n+m+1) len*=2,l++;
	for(int i=0;i<len;i++) r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
    FFT(a,1);FFT(b,1);
    for(int i=0;i<len;i++)
    c[i]=a[i]*b[i];
    FFT(c,-1);
    for(int i=0;i<len;i++)
    c[i].x/=len;
    for(int i=0;i<=n+m;i++)
    printf("%d ",(int)(c[i].x+0.5));
	return 0;
}

这个运行时间就变成了 1.57s。

后记

其实就是觉得直接讲蝴蝶定理比较难以接受，觉得应该在讲蝴蝶定理前先详细思考一下怎么把递归改成数组储存。

但是也有可能是 FFT 作为一个挺绕的算法，不管怎么讲都难以接受？

还有一个事实，很长的讲解根本没有初学者会看，所以 FFT 这种步骤很多，还有很多插入证明，却不能在中间某一步就检测学习成果的算法，真的挺不适合 OI 学习的。。。