网络流的一些证明

本篇由于突然不清楚 最大流、费用流 的算法们为什么对而做。

为什么 FF 是对的

因为反向边有其意义：退流，所以建反向边之后得出的残量网络一定能还原出一个正确的流————只需要把流量设置为反向边的权值即可。

问题在于为什么这个流一定是最大流。OI wiki 上有一个比较简单的证明：

首先，有引理：任意割小于等于任意流。

1.引理的证明：如果把流拆成单位流，也就是说每条边流量为一的流，那么每个单位流都是 \(s\) 到 \(t\) 的一条路径；所以对于任意流和任意割，每个单位流必然经过一条割边。

我们钦定每个单位流对应其经过的一个割边 \((u,v)\)，那么只需要记录每条割边被钦定的次数和，就是这个流的流量。

设 \((u,v)\) 实际被流 \(F(u,v)\) 次，那么它被钦定的次数小于等于 \(F(u,v)\)，又有 \(F(u,v)\le f(u,v)\)，所以每条割边被钦定的次数都小于它的边权。

于是得出结论。

这样我们发现，若一个流 \(F\) 和一组割 \(|S,T|\) 满足 \(F\ge f(|S,T|)\)，则流 \(F\) 必是最大流。其中 \(f(|S,T|)\) 是割的权值。

2.FF 算法的证明：首先在残量网络上肯定可以构造一个割————把能从 \(s\) 到达的部分设为 \(S\)，剩余部分设为 \(T\) 即可。

然后我们有 \((u,v)|u\in S,v\in T\) 在残量网络上流量为 \(0\)。也就是说如果 \((u,v)\) 是正向边则它满流，否则它空流。

而这些满流边的权值和就是割的权值。我们再用之前用过的拆分单位流的方式思考，这样每个单位流中最多经过一个割边，并且如果给由于是满流边，权值为 \(w\) 的边也必然被 \(w\) 个单位流经过。所以每条权值为 \(w_1,w_2,\dots,w_k\) 的满流边总共对应着 \(w_1+w_2+\dots +w_k=f(|S,T|)\) 个单位流，也就是说流量至少为割的权值。

那么根据上面的结论，残量网络对应的流就是最大流。

以及，顺便得出了最小割和最大流一定相等。

为什么 EK 是对的

首先有个经典的觉得 \(FF\) 不对的图：

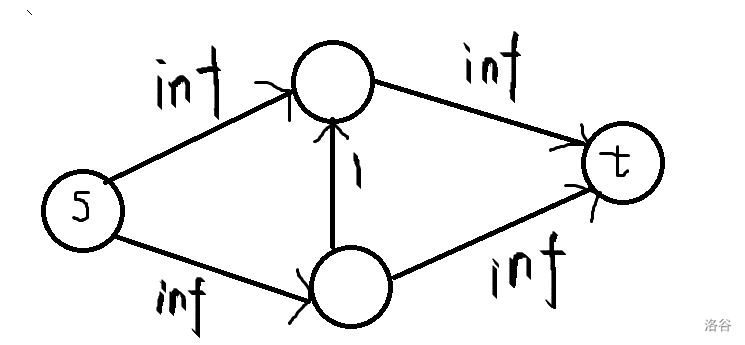
如果每次增广都走中间那条边，会进行 \(2\times inf\) 次增广。

然后我甚至很长时间不知道 EK 的广搜比深搜好在哪，事实上 EK 的正确性来源于广搜选择最短路进行增广。

这里说的最短路当然是每条边边权为 \(1\)，不管正向还是反向。

首先，有引理每次增广的时候每个点的最短路不增，也就是说假设 \(i\) 次增广时残量网络上 \(s\) 到 \(u\) 的最短路为 \(dis_i(u)\)，则 \(dis_{i-1}(u)\le dis_i(u)\)。

我觉得这个东西挺符合直觉的）））

证明如下：假设 \(dis_{i-1}(u)>dis_i(u)\)，那么 \(dis_i(u)\) 这条最短路径上一定有一条边事 \(i-1\) 轮增广当中新出现的，设它为 \(e\) 也就是说 \(i-1\) 轮增广时 \(e\) 的反向边出现在了最短路中。就像这样：

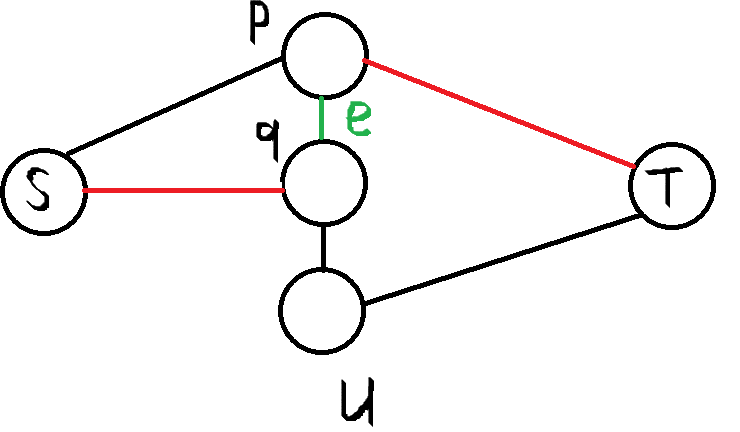
其中红色是第 \(i-1\) 次增广的最短路，黑色是第 \(i\) 次增广的最短路。

这样 \(dis_{i-1}(u)\) 最多是 \(dis_{i-1}(s\rightarrow q)\) 加上 \(dis_{i-1}(q\rightarrow u)\)，而 \(dis_{i-1}(q\rightarrow u)<dis_{i-1}(s\rightarrow t)=dis_i(s\rightarrow p)\)，所以必然有黑色部分不是最短路。

于是我们有了一个类似势能的东西。但是由于有等号，还需要进一步证明。

考虑每次增广必然有一条边流量变为 \(0\)，而流量变为 \(0\) 的边下次再被最短路经过必然为反向边。假设第 \(i\) 次增广时 \((u,v)\) 流量变为 \(0\)，第 \(j\) 次增广时为 \((v,u)\) 方向，那么有 \(dis_i(v)=dis_i(u)+1,dis_j(u)=dis_j(v)+1\)，而由于刚刚的定理，\(dis_j(v)\ge dis_j(u)\)，所以有 \(dis_j(u)\ge dis_i(u)+2\)。也就是说每次增广路都会使一条边不能用，除非下一次使 \(dis_i(u)\) 至少增大 \(2\)。

那么一共只会增广 \(O(|V||E|)\) 次。

所以 EK 的复杂度是 \(O(|V||E|^2)\)。

为什么费用流是对的

1.首先费用流的残量网络在任何时候不会出现负环。

思考原始对偶算法：设计势能函数 \(h_u\) 表示上一轮残量网络里的最短路径，而 \((u,v)\) 的边权被设置为 \(w+h_u-h_v\)，这个是根据松弛不等式 \(h_v\le h_u+w\) 来的嘛，所以最短路上的点，其实新边权均为 \(0\)，而反边权值也是 \(0\)，恰好没有添加负权边。

如果图中出现负环，肯定是没办法设置势能函数的啊，可见图中没负环了）

2.考虑证明算法正确性。反证法，如果我求出的最大流 \(F\) 费用为 \(C\)，而最小费用最大流 \(F'\) 费用为 \(C'\)，那么将 \(F'\) 退掉所有 \(F\) 上的流会发生什么？注意这里退流就是说 \(F\) 里 \((u,v)\) 间流量为 \(f(u,v)\)，则在 \(F'\) 中添加 \(f(u,v)\) 容量的反边。注意是在 \(F'\) 中而不是在残量网络中。

这样一来，由于 \(F\) 和 \(F'\) 都满足流量守恒，那么新图 \(s,t\) 之外每个点容量守恒；而由于两个流都是最大流（用费用流算法求出的肯定是最大流），所以 \(s,t\) 在新产生的图中也容量守恒。

然后，我们把正边和反边均存在的边抵消掉。

接着，图还是容量守恒的，并且应该能划分为若干环。

首先图中肯定没有正环，因为 \(F'\) 可以通过反向给它流量来在不影响最大流的情况下减小花费。原因是这个正环不可能和 \(F'\) 不连通的。

其次图中没有负环，因为这个图事实上是运用完费用流算法后的残量网络的一部分，而残量网络中没有负环，所以也没有负环。

所以这个图必是空图）

由此一来，算法成立。