Dijkstra算法

解决问题

单源最短路问题：

给定一个带权有向图G=(V,E)，其中每条边的权是一个实数。另外，还给定V中的一个顶点，称为源。要计算从源到其他所有各顶点的最短路径长度。这里的长度就是指路上各边权之和。这个问题通常称为单源最短路径问题。

算法过程

它只适用于求解正权（有负权边都不行！）图中的最短路，但是十分稳定且快速（堆优化后为 \(O(m log m)\)）。

普遍理解方式是贪心。将结点分成两个集合：已确定最短路长度的（确集），未确定的。最初确集里只有源。然后每次对那些上一次被加入确集的结点的所有出边执行松弛操作。从未确定集合中选取一个最短路长度最小的结点，移到第一个集合中。直到全部进入确集，即全部确定。总共移动 \(V\) 次，每次求最小为 \(O(n)\) ,总复杂度为 \(O(n^2)\)。

正确性

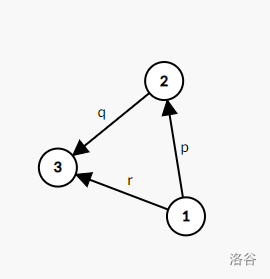
如图，1号为源。如果3号最短路不为 \(r\) ，则存在 \(p+q<r\) 由于没有负边，所以必定有 \(p<r\) ，则3号不会先进入确集，故不是最短路不会进入确集，是最短路才进入，确集正确。

个人理解

但我们注意到这算法中也有一个松弛。那么，应该还有一种理解方式。指的是在对全图进行一次遍历的松弛操作时，其中除源外 \(dis\) 最小的点的最短路一定是正确的，证明同上。那么我们每松弛一次，找到最小的并删掉此点，进行下一次松弛。接着可以发现，仅需要对距离删掉的点一次松弛可到达的边松弛不影响正确性，因为其它的点也不可能是 \(dis\) 最小的（由于正权）。

优化

由于每次求最小，适合使用数据结构堆。这优化了最小最短路查询至 \(O(1)\) ,但每个点入堆需要 \(O(logn)\) 次。于是乎很多人认为它的复杂度是 \(O(m+nlogn)\) ,这是不正确的。原因在于，未优化的算法直接改变最短路的值，但在堆中，不支持删除某一个数据，故把一个点的最短路改变及会改变堆的性质，它就不是堆了！解决方法需要每次每个点被松弛都入一次堆，那么我们入队时需要知道此数据对应点和此时最短路，故需要同时入堆两个值。需要注意的是，一个点会多次出堆，如果出堆的点已经在确集中，那么继续出堆。按照这种方法，\(m\) 次松弛各入堆一次，时间复杂度为 \(O(mlogm)\)（还有出堆m次）。

板子AC CODE

P4779 【模板】单源最短路径（标准版）←卡了SPFA

//Dijkstra 手打堆+前向星实现
#include<bits/stdc++.h>
using namespace std;
int ll;
struct dui
{
    int s;		//长度 
    int an;		//点名称 
}d[100005];		//堆 
struct qxx
{
    int next;		//下一边编号 
    int len;		//边权 
    int to;		//指向节点 
}a[500005];		//前向星 
int head[100005],mi[100005],x;		//头边编号、最短路 
bool ct[100005];		//是否在确集中 
void cha(int x,int y)		//堆插入 
{
    ll++;
    d[ll].an=x;
    d[ll].s=y;
    int er=ll,ba=er/2;
    while(ba>=1&&d[er].s<=d[ba].s)
    {
        int q=d[er].s;
        d[er].s=d[ba].s;
        d[ba].s=q;
        int p=d[er].an;
        d[er].an=d[ba].an;
        d[ba].an=p;
        er=ba;
        ba=er/2;
    }
    return;
}
int chu()		//返回堆中最大s对应的an 
{
    int ss=d[1].an;
    d[1].an=d[ll].an;
    d[1].s=d[ll].s;
    ll--;
    int ba=1,er=ba*2;
    while(er<=ll)
    {
        if(er+1<=ll&&d[er+1].s<=d[er].s) er++;
        if(d[er].s>d[ba].s) break;
        int q=d[er].s;
        d[er].s=d[ba].s;
        d[ba].s=q;
        int p=d[er].an;
        d[er].an=d[ba].an;
        d[ba].an=p;		//不会swap 
        ba=er;
        er=ba*2;
    }
    return ss;
}
int main()
{
    int n,m,st,aa,bb,cc;
    cin>>n>>m>>st;
    memset(head,-1,sizeof(head));
    memset(mi,0x5f,sizeof(mi));		//0x5f非常大，但此值比INT_MAX小 
    memset(ct,0,sizeof(ct));
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&aa,&bb,&cc);
        a[i].to=bb;
        a[i].len=cc;
        a[i].next=head[aa];
        head[aa]=i;		//连边 
    }
    x=st;
    mi[st]=0;
    ct[st]=1;		//源点进入确集 
    for(int i=2;i<=n;i++)		//需要把 n-1 个点加入确集 
    {
        for(int j=head[x];j!=-1;j=a[j].next)
        {
            if(ct[a[j].to]==0&&mi[x]+a[j].len<mi[a[j].to])		//不在确集中
            {
                mi[a[j].to]=mi[x]+a[j].len;		//松弛 
                cha(a[j].to,mi[a[j].to]);
				//由于不能更改堆内部元素权值，只能每次单独插入一组值 
            }
        }
        x=chu();		//最小值进入确集，下次以其为始松弛 
        while(ct[x]) x=chu();		//由于堆内有重复元素，所以重复点可能多次出队 
        ct[x]=1;		//进入确集
    }
    for(int i=1;i<=n;i++) printf("%d ",mi[i]);
    return 0;
}
//O(m log m)

算法优越性

只能在正权图中使用！目前已知最快的稳定单源最短路算法，但代码较长，尤其是不用 \(STL\) 时。所以我个人觉得数据随机正权图用SPFA更好（懒）。

补充

我时至今日SPFA才第一次真正被卡了，感受到了Dijkstra的用途之大。大多数时候，手写堆是浪费时间的，在此奉上STL堆实现Dijkstra。

void Dijkstra(int st)
{
	priority_queue<pair<int,int> > q;
    memset(ct,0,sizeof(ct));
    x=st;mi[st]=0;ct[st]=1;
    for(int i=2;i<=n;i++)
    {
        for(int j=head[x];j!=-1;j=a[j].next)
        {
            if(ct[a[j].to]==0&&mi[x]+a[j].len<mi[a[j].to])
            {
                mi[a[j].to]=mi[x]+a[j].len;
                q.push(make_pair(-mi[a[j].to],a[j].to));
            }
        }
        x=q.top().second;
		q.pop();
        while(ct[x])
        {
        	x=q.top().second;
			q.pop();
		}
        ct[x]=1;
    }
}