连通性算法

1.连通性问题

一些定义：

在有向图中对于图中的任意两个节点 \(u,v\)，存在一条路径由 \(u\) 到 \(v\)，则称 \(u\) 可达 \(v\)；在无向图中任意两个节点 \(u,v\)，存在一条路径由 \(u\) 到 \(v\)，则称 \(u,v\) 两点联通。

一张无向图存在一个子图任意两点联通，则称之原图的一个为连通块即连通分量；一张有向图存在一个子图任意两个点互相可达，则称之为一个强连通分量，若将有向边替换为无向边则相互可达，则称之为一个弱连通分量。

在无向图中，去掉一条边使连通块数目变多，即使一些原图中联通的点不连通，则称之为桥；去掉一个点使原图连通块数变多，则称之为一个割点。

一个没有割点的无向图为点双联通图，一个没有桥的图为边双连通图。

很多连通性问题都需要求解它们。

2.强连通分量

解决问题为分割极大强连通分量，及任何一个强连通分量都不可能扩大。塔扬算法依靠DFS生成树的诸多信息实现求解。

DFS生成树

用DFS遍历一张图，会形成DFS生成树。有向图中，遍历过程中有没有形成环的边（不代表不在环中）树边，由祖先向后代的边前向边，由后代向祖先形成环的返祖边，以及在树枝之间的横叉边。

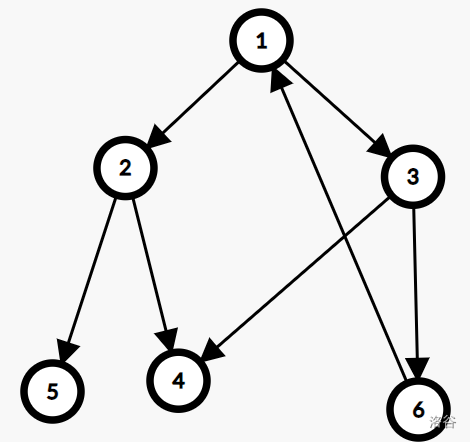
上图中若从1开始够早生成树，则4至3的边是横叉边，6至1的边是返祖边，其它均为树边。

由于我们想保存的是连通性信息，故而从一个点开始只有能遍历的点对于它的有意义，所以有向图中并不要求一个弱联通子图内的点全部在一棵DFS生成树中。

顶点

我们定义dfn为点的DFS序，同时定义一个极大强连通分量中dfn值最小的点为强连通分量的顶点。

首先，极大强连通分量在DFS生成树上一定是联通的。

证明：设我们有一个DFS生成树上不连通的强连通分量，则至少有两部分由非树边相连。若此边为返祖边，则强连通分量可扩展（因为出现环）成为更大的强连通分量，矛盾（如下图1）；若此边为横叉边，则那个顶点想回到此点必然经过两点LCA才能回到此点（因为横叉边只在后遍历的枝条向先遍历的枝条间有，故横叉不能反向走），也可扩展为更大的强连通分量（如下图2）

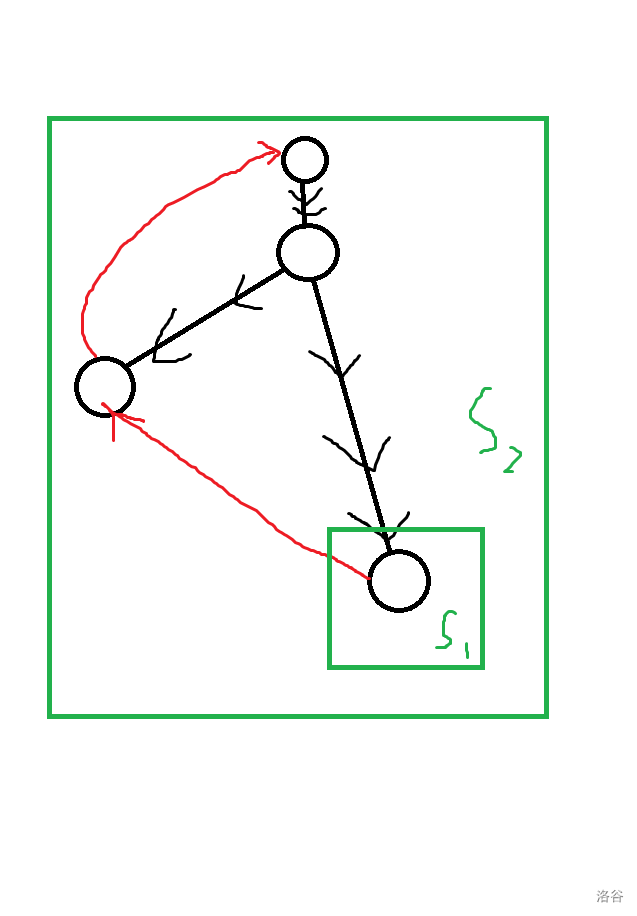
dfn值与low值

那么，我们可以搜索过程中维护一个栈，遇到顶点则将该强连通分量中的点全部弹栈，这样，遇到一个顶点的时候，栈中它子树内所有点和它所在的强连通分量一一对应，这是因为子树外的点不符合顶点的定义，不在栈中的点一定属于另一个强连通分量。

所以，我们的问题变成了求顶点。一个点不是顶点有两种情况。

1. 它的子树内存在指向它祖先的返祖边（同上图1）

2. 它的子树内可通过一条返祖边到达一个不在栈中的点（同上图2）

那么，我们定义low值为一个点即其子树中经过一条（返祖、横叉）边可到达的dfn值最小的不在栈中点的dfn值。由上当且仅当 \(dfn=low\) 一个点才是顶点。更新此值时，若遇到儿子（不需要考虑前向边），则用low值更新；若遇到子树外的点，则用dfn值更新。

这样，我们设计了 \(O(n+m)\) 的算法。

代码：

void make(int i)
{
    now++;
    while(zh[mz]!=i)
    {
        e[zh[mz]]=now;si[now]++;
        c[zh[mz]]=0;
        mz--;
    }
    e[zh[mz]]=now;si[now]++;
    c[zh[mz]]=0;
    mz--;
}
void dfs(int u)
{
    low[u]=dfn[u]=++tot;
    zh[++mz]=u;c[u]=1;
    for(int i=head[u];i!=-1;i=a[i].next)
    {
        int v=a[i].to;
        if(dfn[v]==-1) dfs(v),low[u]=min(low[u],low[v]);
        else if(c[u]==1) low[u]=min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u]) make(u);
}

3.割点和桥

顾名思义，求割点和求桥

DFS生成树

可以相比有向图的生成树。但是，若存在横叉边，则指向的那个点会在先遍历的枝条中被遍历，以上面的图为例，无向图情况下，3会成为4的儿子。由此可知无向图中只有返祖边（即前向边）和树边。

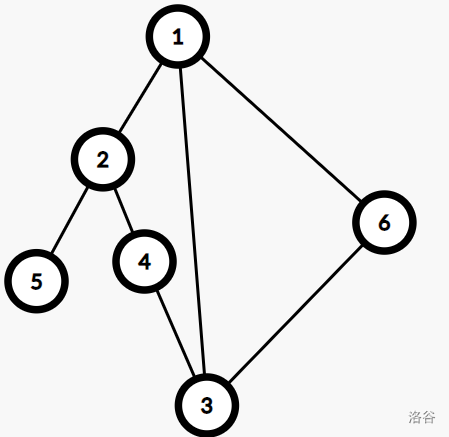
于是，无向图中环的情况更加方便表示，即一个返祖边生成一个环

常规算法

对于桥，我们发现桥显然不在环中，故而一条返祖边在树上对应的路径上的边不为桥，使用树上差分即可维护。

对于割点，它连接的所有树边中一定有一些没有办法不经过该点（指经过一些返祖边）到达另一些。我们将建立并查集，对于一条返祖边，其路径上对应的那些边可以直接合并。最后，如果一个点的出边全属于一个连通块，则它不是割点。

这两个算法也是 \(O(n+m)\) 的，但好像不怎么常用。

Tarjan算法

我们仍然定义dfn值为点的DFS序。这次，没有横叉边的干扰，只有返祖边才能产生环，我们直接定义low值为不经过父亲节点能够经过的最小dfn值，这里和有向图情况不完全相同（实际上这个重名好像是翻译问题）

这时，若每个儿子都有 \(low_{v}<dfn_{u}\) ，则它不是割点。特殊的，对于选定的根，只要有两个儿子，就是割点。桥则相似，若一条树边有 \(low_{v}>dfn_{u}\) 则为桥，而返祖边不可能为桥。

更新low只需要对于树边，用儿子的low更新；对于返祖边，用dfn更新即可。

这里有一个很有趣的事情，low[u]=min(low[u],dfn[v]) 这句话，在求强连通分量时可以改为 low[u]=min(low[u],low[v])，但是求割点时却不行。这时因为求强连通分量时，此种情况u和v一定在同一强连通分量中，故不会影响顶点。而此题中要的保证的是不经过父亲，而如果从祖先再向下走树边便不能保证了。

双连通分量

差不多的，可以证明点双和边双都是在DFS生成树上联通的。在跑Tarjan求割点和桥的时候加点+弹栈就行了。特殊地，求点双连通分量时割点不用弹栈。