DP优化

• \(DP\) 是很常见的一种算法，其重点在于转移式的设列，但 \(DP\) 实现后的优化也很重要，不过优化大部分都有套路性，这里列举一些我的认知。

树状数组维护转移条件

• 例题：奶牛行动

这道题设 \(f_i\) 表示前 \(i\) 位的方案数，设 \(s_i\) 为前缀和，则显然有转移方程：

\[f_i=\sum\limits_{j=0}^{i-1}a_i\times(s_i-s_j\geqslant0) \]

时间复杂度为 \(O(n^2)\) ，考虑如何优化，因为有一个奇怪的限制条件，从常规角度看较为复杂，但可以转变思路，把 \(f_i\) 看做以 \(s_i\) 为下标（可以先离散化），则可转移状态在这样的数组中为一段，求和自然可以使用树状数组。这样时间复杂度就被减低到了 \(O(n \log n)\)。

单调队列优化

决策类DP，指对于每一个状态 \(f_i\) 都由决策区间内的一个决策点 \(j\) 转移而来，这类DP转移实际发生次数为线性级别，故而较易于优化。

• 例题1：P2254 [NOI2005] 瑰丽华尔兹

这道题的DP情况较多，原本的三维DP \(f_{i,j,k}\) 表示在 \((i,j)\) 这个点上在第 \(k\) 段时间后最多能行进距离。原题中有四中方向，会使转移式产生不同，但实现方式相同，这里以向右为例。时间段 \(k\) 我们枚举每一行 \(i\) ，先不考虑障碍物，则有：

\[f_{i,j,k}=\min\limits_{l=j-(t-s+1)}^{l-1} f_{i,l,k-1}+j-l+1 \]

这里的实现方式也是 \(O(n^2)\) ，我们试着优化，优化思路是省去无用的状态。考虑如果决策区间内存在 \(a_1\geqslant a_2\) 且由 \(a_2\) 决策（即充当 \(l\)）比 \(a_1\) 更优时，\(a_1\)不会起到作用，又由于 \(j-(t-s+1)\) 单调递增，故一个无用决策不会再次生效，即可用单调队列维护。如果遇到障碍，清空队列即可。

• 例题2：有限背包问题

题意：01背包的基础上，每个物品有 \(m[i]\) 件。

当然可以把多件物品二进制拆分为 \(\log m[i]\) 个物品，但我们更希望出现一个线性做法。

我们看看暴力转移的方程，设 \(f_{i,j}\) 表示取前 \(i\) 个物品的价值为 \(j\) 时的最小代价（因为原题价值小重量大）

\[f_{i,j}=\min\limits_{k=1}^{m[i]} f_{i-1,j+k\times p[i]}+k\times w[i] \]

此时，由于决策点并非区间形式，不方便进行优化，故我们按上一层状态第二维模 \(p[i]\) 的结果将 \(i-1\) 一层的状态分类转移，则每个种类中都可以使用单调队列优化，得到最终复杂度为 \(O(n)\) 。

• 单调队列优化的适用式如下：

\[f_i=\min\limits_{j=g(i)}^{i-1} p(j) \]

满足三点：\(j\) 的取值是连续的区间，左端点 \(g(i)\) 单调不降，取最值。

斜率式优化

面对一个转移式与 \(i,j\) 均有关的 \(DP\) ，我们可以试着整理式子。

• 例题1：[ZJOI2007]仓库建设

设 \(f_i\) 为 \(i\) 处建立仓库，其之上的最小代价，显而易见

\[f_i=\min\limits_{j=0}^{i-1} c[i]+dp[j]+\sum_{k=j+1}^{i}p[k]\times (x[i]-x[k]) \]

前缀和设 \(s_i\) 为 \(x\) 的前缀和，\(sum_i\)为 \(x\times p\) 的前缀和，则

\[f_i=\min\limits_{j=0}^{i-1} \{f_j+x[i]\times(s_i-s_j)+(sum_i-sum_j)\}+c[i] \]

对于两个状态 \(j\) 和 \(k\) 我们若有

\[f_j+x[i]\times(s_i-s_j)+(sum_i-sum_j)<f_k+x[i]\times(s_i-s_k)+(sum_i-sum_k) \]

设对于本次转移，两个状态 \(j\) 优于 \(k\) 。整理这个不等式，将含有 \(i\) 项放到同一侧，则有

\[(f_j-sum_j)-x[i]\times s_j<(f_k-sum_k)-x[i]\times s_k \]

\[x[i]\times(s_k-s_j)<(f_k-sum_k)-(f_j-sum_j) \]

这个时候，我们规定左边一项 \(s_k-s_j\) 为正，则有

\[x[i]<\frac{(f_k-sum_k)-(f_j-sum_j)}{s_k-s_j} \]

这里右边是一个斜率式，将每一个状态看作一个点 \((s_i,f_j-sum_j)\) ，则若两点的连线斜率大于 \(x[i]\) ,横坐标较大的不可能成为决策点。

所以如下情况时

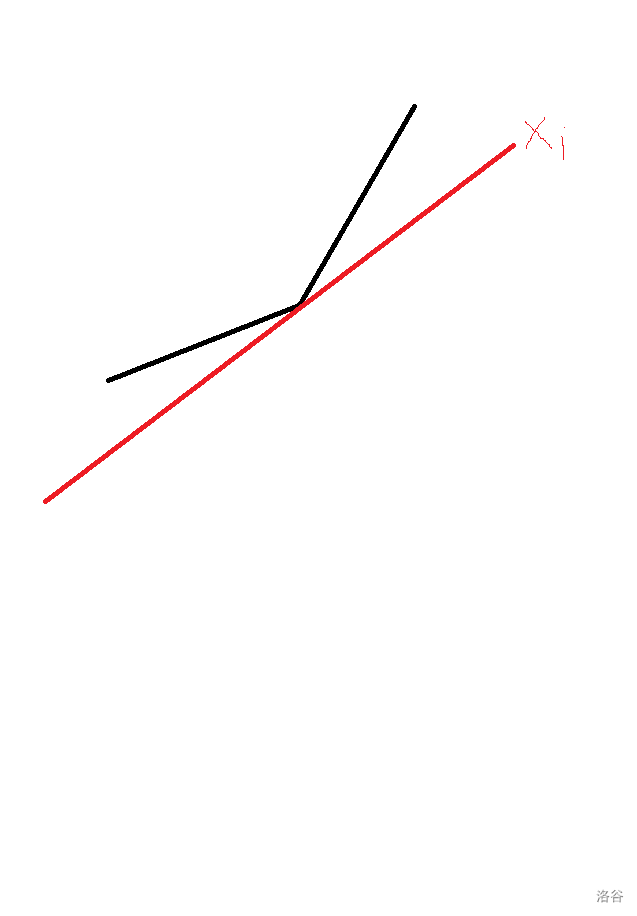
则会有中间的状态优于右边，同时优于左边，即为最优。

根据这个原理，在写出所有点时只有下凸壳上的点可能成为最优状态。由于横坐标单调，故而下凸壳可以用单调栈维护。本题中，决策斜率 \(x[i]\) 也单调，故而可以使用单调队列维护当前斜率大于决策斜率的凸壳，其中队头则为决策点。

如果决策斜率不单调，我们可以用单调栈存下凸壳中所有点，然后在凸壳上二分寻找决策点。

• 例题2：NOI2007货币兑换

题意经过转换会发现每一次操作必定花光所有钱或金券，可以设 \(f_i\)表示当天拥有的最多钱数（不管买不买金券）则有

\[f_i=\max\{f_{i-1},\max\limits_{j=1}^{i-1}A_iX_j+B_iY_j\} \]

其中\(X\)和\(Y\)都是确定的当天兑换券数。

不看\(f_{i-1}\)把这个式子化为斜率式时，由于有两项含有 \(i\) 可以同时除掉一个变为一项。得到

\[\frac{A_i}{B_i}>\frac{y_k-y_j}{x_k-x_j} \]

成立条件是 \(x_k>x_j\) ，不是 \(k>j\) 了。

此时，我们已然可以维护上凸壳，但新插入的点可能在任意方位，故而需要使用李超线段树或平衡树维护凸壳。

如果不想用这些数据结构，则需要按横坐标排序，之后有编号靠前的状态才能对后面的状态做贡献，符合CDQ分治应用条件，故而可以使用CDQ分治将凸壳断为几段后求最大。

需要注意的是如果横纵坐标和 \(f\) 有关系，则分治时必须先递归再操作。

• 斜率优化的应用式如下：

\[f_i=\min\limits_{j=1}^{i-1} x_js_i-y_j \]

此时是

\[y_j=x_js_i-f_i \]

相当于求截距的最值，故而凸壳维护相切。但这种斜率式较为复杂于推导，上文的斜率式更易于推导。

决策单调性优化

• 先给出应用式

\[f_i=\min\limits_{i=1}^{i-1} f_j+s_{i,j} \]

设 \(k_i\) 为状态 \(i\) 的决策点。

满足四边形不等式对于 \(l_1\leq l_2\leq r_1\leq r_2\) 都有 \(s_{l_1,r_1}+s_{l_2,r_2}\geq s_{l_1,r_2}+s_{l_2,r_1}\) 时则有决策点单调不降，即对于 \(i<j\) 有 \(k_i\leq k_j\)。

反证设 \(k_i>k_j\),则有 \(k_j<k_i<i<j\)，同时有\(f_{k_j}+s_{k_j,j}\leq f_{k_i}+s_{k_i,j}\)

此时应用四边形不等式得到 \(f_{k_j}+s_{k_j,i}\leq f_{k_i}+s_{k_i,i}\) 即 \(k_j\)应为 \(i\) 的决策点，故矛盾。

• 例题：NOI2009诗人小G

设 \(f_i\) 表示到此分一行，前 \(i\) 个字符的最小代价，容易列出DP式

\[f_i=\min\limits_{j=0}^{i-1} f_j+|sum_i-sum_j+i-j+1-L|^P \]

其中函数 \(s_{i,j}=|(sum_i+i)-(sum_j+j)+(1-L)|^P\) .

我们考虑函数 \(k_s=|s-m|^P\) ，它的导函数是单调的，即差分是单调的，故而有 \(w_{i,j}\) 满足四边形不等式，则 \(k(w_{i,j})\) 也满足四边形不等式（感性理解qwq）。

由于 \(sum\) 是前缀和满足四边形不等式，则 \(s\) 满足四边形不等式。

我们的定理告诉我们决策点是单调不降的，但依据此直接更新复杂度仍然为 \(O(n^2)\) 。此时，我们考虑更新决策点函数 \(k\) 。

根据定理，一个被更新的决策会存在一个“转折点”，将之后所有的 \(k\) 函数值更新为当前状态。故而，可以使用单调栈存储区间，每个区间表式此段状态决策点为同一个值，如

\[11111111111111111111111111111111222223333356 \]

此时对于一个新的状态，从栈顶开始向前搜索寻找第一个开始节点比当前节点优秀的决策点，否则覆盖后面所有决策点为当前状态。找到后，在该决策点代表区间内二分寻找“转折点”，之后分裂决策点即可。

更新时，栈中区间右端点在当前状态前的状态可以直接弹出，故用单调队列维护即可，每个状态弹栈只有一次，加上二分，复杂度为 \(O(n \log n)\)

矩阵乘法/卷积优化

我认为这两者可以放在一起考虑，因为两者都是把模式相同的转移转化为有结合律的运算（乘法），再用快速幂解决，形式化描述条件大概为

1. 状态中有一维的转移范围是固定的

2. 转移式不随着该维度的移动而移动

3. 此维较大（尤其是矩阵乘法）

如果这个转移式中不涉及到两个状态相乘，则可以使用矩阵乘法。

如果转移中涉及到方案数之类，比如两种方案数相乘转移到两种方案合并方案数，则可以使用卷积。若合并为位运算，可以考虑FWT；若合并为相加运算，可以考虑FFT（NTT）。

结语

对于DP，优化大部分是非常套路的，所以学习一下还是很有用的。