支配树算法

1.支配树问题

对于一张有向图，定义一个起点 \(S\)，若删去一个点 \(u\),则使起点 \(S\) 不可到达 \(v\)，则称为 \(u\) 支配 \(v\)。

性质1：显然有若 \(u\) 支配 \(v\)，\(v\) 支配 \(w\)，则有 \(u\) 支配 \(w\)。

性质2：每个点的所有支配点中存在且仅存在一个最近支配点使得其它所有支配点都是它的支配点。反证显然。

性质3：将每个点的最近支配点向它连一条边，则形成以 \(S\) 为根节点的外向树，由前两点显然。我们称这棵树为支配树。

2.特殊DAG

看到有向图的连通性算法，果断从起点建立dfs生成树。对于一类DAG图，生成树中只含有树边和前向边，我们想到这和无向图的割点算法极为相似。

用类似的想法考虑，对于一条前向边 \(u->v\)，这条链上除 \(u\) 外的所有点都不可能是 \(v\) 的支配点。对于每一个点 \(x\)，记录连向它的点钟深度最小的，称为半支配点 \(k\)，令 \(x\) 到 \(k\) （不包含k）中半支配点深度最小的为\(u\)，则有:

1.当 \(x=u\) 时，\(x\) 的支配点就为 \(k\)。

2.当 \(x=u\) 时，\(x\) 的支配点为 \(u\) 的支配点

这样可以快速维护（其实这不重要）

3.Lengauer-Tarjan算法

对于任意有向图的支配树求解，可以使用此算法快速求解。

对于任意有向图，如何转化为支配关系相同的DAG呢？此算法提出了精髓的半支配点构造方法，令一个点 \(x\) 的半支配点为 \(dfn\) 最小的 \(k\)，使得存在一条从 \(k\) 到 \(x\) 的路径，使路径上除了端点外每一个点 \(u\) 都有 \(dfn_u>dfn_x\)。

考虑为什么这种构造等效。

首先，一定有 \(dfn_k<dfn_x\)，更进一步，半支配点一定在 \(x\) 到根的链上。因为若不在此链上，则必然可以向上找到更小的解。

其次，由 \(k\) 到 \(x\) 存在路径使得没有任何节点为生成树两点之间的边，是等效产生一条前向边的充要条件，而横叉边必然由 \(dfn\) 大的点连向 \(dfn\) 小的，故而此路径上中间所有点 \(u\) 必然有 \(dfn_u>dfn_x\)。外加半支配点为所有满足条件的点中 \(dfn\) 最小的，故而与DAG情况中半支配点等效。

于是，求解半支配点后即可转化为DAG形态进行求解。

4.求解半支配点

对于 \(u\)，建反向图来枚举 \(v\)，存在边 \(v->u\)

1.若 \(dfn_v<dfn_u\)，则用 \(v\) 可以更新半支配点。

2.若 \(dfn_v>dfn_u\)，则 \(v\) 与 \(u\) 的LCA到 \(v\) 的路径（不包含LCA）上，必有所有点的 \(dfn\) 都大于 \(dfn_u\)。更进一步，任何一个点的半支配点到这个点的路径再到 \(u\) 的路径也符合半支配点的条件，故可以用v的祖先中半支配点dfn最小的点的半支配点更新半支配点。

那么，将 \(dfn\) 由大到小枚举，对于每一个点开一个带权并查集，来更新每个点其到根的链中当前搜索到的所有点中半支配点最小的点。这样，在枚举时，正好每个并查集中存的是LCA的儿子的子树，每个点的权值也正好是到LCA的儿子的链的值（如下图）

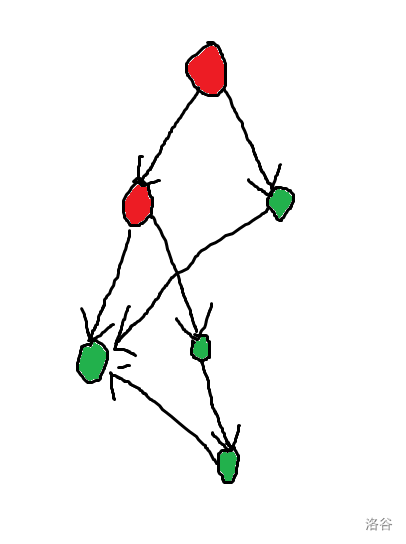
特殊地，没搜到过的点的并查集中只有一个点，所以代码实现时无需分类讨论。

关于带权并查集，由于维护链上信息而不是总体信息，不能直接合并到根，故每处理完一个点后，将它并查集的父亲改为原图中的父亲即可，单次复杂度为 \(\log n\)。

5.求解支配点

回想DAG图中的求法，主要需要维护每个点到半支配点中的点中半支配点最小的点。我们注意到，求解半支配点的过程中，同样是维护一段链中半支配点最小的点。在搜索到 \(x\) 时，\(fa_x\) 的已搜到的儿子的子树中的点的权值是到 \(fa_x\) 的儿子的权值。（如下图）故其中存在半支配点为 \(fa_x\) 的点时，可以更新。

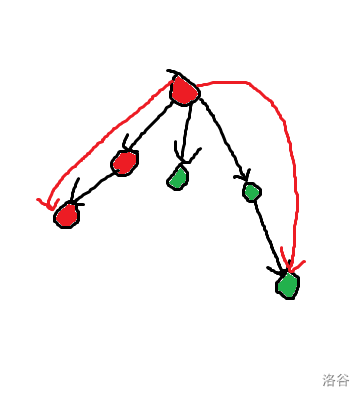
存在一个问题，半支配点的枚举为 \(dfn\) 倒序，故而在求解一个点的支配点时为第二种情况（见DAG）时，并不确定 \(u\) 的支配点。可行的方法是，将 \(u\) 存下，最后更新。

6.模板code

图论这种暴力讨论的代码是真的恶心……

#include<bits/stdc++.h>
using namespace std;
struct qxx
{
	int to,next;
}a[1000005];
int head[3][200005],cnt,n;
void add(int id,int aa,int bb)
{
	a[++cnt].to=bb;
	a[cnt].next=head[id][aa];head[id][aa]=cnt;
}
int dfn[200005],re[200005],tot,fa[200005];
void dfs(int u)
{
	re[dfn[u]=++tot]=u;
	for(int i=head[0][u];i!=-1;i=a[i].next)
	{
		if(dfn[a[i].to]) continue;
		fa[a[i].to]=u;dfs(a[i].to);
	}
}
int idom[200005],sdom[200005];
int f[200005],mi[200005];
int find(int x)
{
	if(x==f[x]) return x;
	int now=find(f[x]);
	if(dfn[sdom[mi[f[x]]]]<dfn[sdom[mi[x]]]) mi[x]=mi[f[x]];
	return f[x]=now;
}
int ans[200005];
void get_sdom()
{
	for(int d=n;d>=2;d--)
	{
		int u=re[d];
		for(int i=head[1][u];i!=-1;i=a[i].next)
		{
			int v=a[i].to;
			if(!dfn[v]) continue;
			int tmp1=find(v);
			if(dfn[sdom[mi[v]]]<dfn[sdom[u]]) sdom[u]=sdom[mi[v]]; 
		}
		f[u]=fa[u];
		add(2,sdom[u],u);
		int x=fa[u];
		for(int i=head[2][x];i!=-1;i=a[i].next)
		{
			int y=a[i].to;
			if(!dfn[y]) continue;
			int tmp1=find(y);
			idom[y]=(dfn[sdom[mi[y]]]==dfn[x]?x:mi[y]);
		}
		head[2][x]=-1;
	}
}
void get_idom()
{
	for(int d=2;d<=n;d++)
	{
		int u=re[d];
		if(sdom[u]!=idom[u]) idom[u]=idom[idom[u]];
	}
	for(int d=n;d>=2;d--)
	{
		int u=re[d];
		ans[idom[u]]+=ans[u];
	}
}
int main()
{
	memset(head,-1,sizeof(head));
	int m,aa,bb;
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d",&aa,&bb);
		add(0,aa,bb);add(1,bb,aa);
	}
	for(int i=1;i<=n;i++) mi[i]=sdom[i]=f[i]=i,ans[i]=1;
	dfs(1);
	get_sdom();
	get_idom();
	for(int i=1;i<=n;i++) printf("%d ",ans[i]);
	return 0;
}

7.总结

复杂度 \(O((n+m)\log n)\)。