置换群相关计数/Burnside引理

Burnside引理用于解决等价类数量问题。

1.置换

将有某种顺序的集合里的元素交换顺序的运算为置换，例如 \((a,b,c,d)\) 经过 \(\begin{pmatrix}1,2,3,4\\2,3,4,5\end{pmatrix}\) 这个置换后就会变成 \((b,c,d,a)\) 。

容易知道，置换满足交换律，结合律，且有单位元（即不变的置换），有逆元（将置换反过来做），这样一些置换可以构成一个群。

2.Burnside引理

现在给定 \(n\) 种方案和大小为 \(m\) 的置换群 \(G\) ，经过给定的置换群中某些置换各一次之后相等的方案属于同一个等价类。

以三元环黑白染色为例

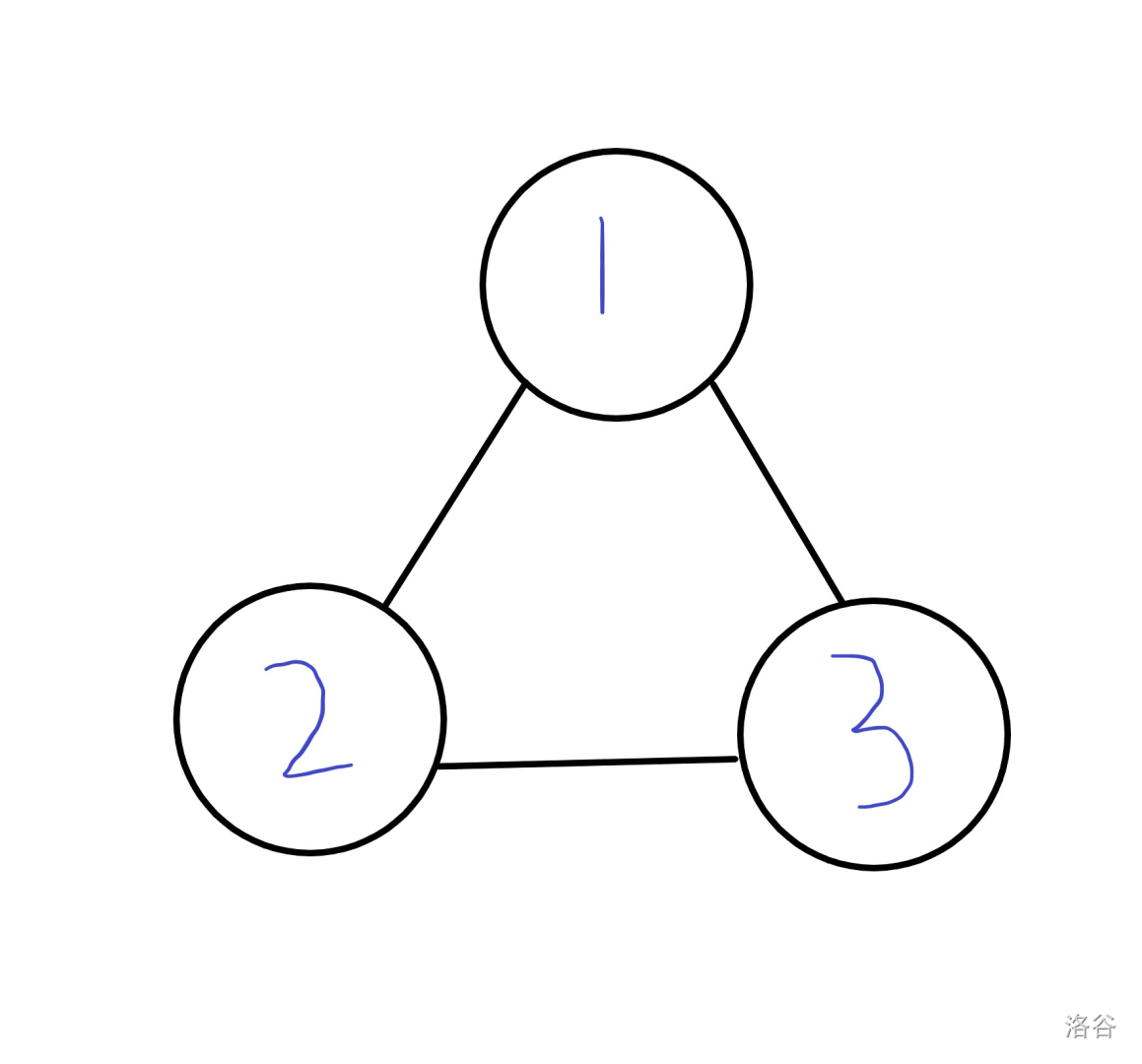
用123节点的颜色表示一种方案，则答案的四个等价类为 \(\{111\},\{000\},\{100,010,001\},\{110,011,101\}\) 。

设方案 \(i\) 所属的等价类为 \(E_i\) ，因为置换群内存在逆元，所以所有 \(E_i\) 内的元素所属的等价类也为 \(E_i\) ，于是设等价类数为 \(x\) ，则有 \(\sum_{i=1}^x |E_i|=n\) ，并且等价类集合的并集为方案集合。

设方案 \(i\) 对应一个置换集合 \(Z\) ，使得 \(i\) 经过任意 \(z_j\) 变换后仍为本身，即置换后不变的集合，则有对于任意方案 \(i\) ，\(|E_i|\times |Z_i|=m\) 。因为根据置换的结合律，若 \(i\) 经过两个不同的置换 \(G_j,G_k\) 后相等，则必然有 \(G_k\) 可由 \(G_j\) 与 \(Z_i\) 中的置换得到。反之，对于一个 \(G_j\) ，任何 \(Z_i\) 中的置换都可以和其一起产生一个重复的方案。于是，不重复的方案乘上使其不变的方案数即为重复的方案数。

可以得到

\[\sum_{i=1}^n |Z_i|=\sum_{i=1,j\in E_i}^x|E_j|\times|Z_j|=x\times m \]

为了方便统计，我们设 \(X_i\) 为经过 \(G_i\) 置换后不变的方案数，则 \(\sum_{i=1}^n |Z_i|=\sum_{i=1}^m X_i\)

于是，有 \(x=\frac{\sum_{i=1}^m X_i}{m}\) ，即为Burnside引理。

3.pólay定理

有很多求本质不同的染色方案数的题目，它们可以使用Burnside引理解决。

以四元环黑白染色为例，置换为顺时针旋转0个，旋转1个，旋转2个，旋转3个。旋转零个不会产生改变，\(X_0=2^4=16\) ；旋转一个只有四个点同色才不变，\(X_1=2\) ；旋转两个则位置1,3互换，2,4互换，两者不相关， \(X_2=2^2=4\) ，旋转三个和旋转一个相同 \(X_3=2\)。

得到答案为 \(\frac{16+2+4+2}{4}=6\) 。

我们发现一个置换由若干个不相干的部分组成，如 \(\begin{pmatrix}1,2,3,4,5\\4,5,1,3,2\end{pmatrix}\) 由 \((1,3,4)\) 与 \((2,5)\) 组成。我们设一个置换所能分割成的部分数为 \(c(g)\) ，则 \(X_g=col^{c(g)}\) ，其中 \(col\) 为染色的颜色数。

于是可以改进Burnside引理得到 \(x=\frac{1}{m}\sum_{i=1}^m col^{c(X_i)}\)