从行列式到矩阵树定理

1.行列式求值

对于一个排列 \(p\) ，设 \(\tau(p)\) 为排列的逆序对数，则对于一个 \(n\times n\) 的矩阵 \(A\) ，定义它的行列式 \(\det(A)\) 为

\[\det(A)=\sum_{p} (-1)^{\tau(p)} \prod_{i=1}^n a_{i,p_i} \]

其中 \(p\) 为任意一个长度为 \(n\) 的排列。

求行列式的值，需要用到排列的一个性质，即交换排列 \(p\) 的两个元素，则 \(\tau(p)\) 的奇偶性一定改变，因为设交换 \(p_i\) 和 \(p_j\) ，则偏序发生改变的数对除了 \((p_i,p_j)\) ，下标在 \(i,j\) 之间且值在 \(p_i,p_j\) 之间的所有值，都会和 \(i,j\) 产生两次贡献，于是总产生贡献次数为奇数，奇偶性改变。

这样可以得到行列式的一些性质：

• 矩阵转置后行列式不变，将所有排列转置即可。

• 交换矩阵的两行，行列式变为相反数。相当于每个排列逆序对奇偶性改变。

• 矩阵的一行整体乘上 \(k\) ，行列式也乘上 \(k\) 。因为每个排列必然经过每一行一次，所以每个排列贡献乘一次 \(k\) 。

• 若矩阵 \(A,B,C\) ，在某行 \(i\) 满足 \(a_{i,j}=b_{i,j}+c_{i,j}\) ，其余位置均满足 \(a_{i,j}=b_{i,j}=c{i,j}\) ，则 \(\det(A)=\det(B)+\det(C)\) 。证明和上一条类似。

• 若矩阵 \(A\) 有两行 \(i,j\) ，满足 \(a_{i,k}=x\times a_{j,k}\) ，则 \(\det(A)=0\) ，因为交换两行后行列式值为相反数，将 \(i\) 行同时乘 \(x\) ， \(j\) 行同时除 \(x\) 后行列式值不变，而两者相等，则均为零。

• 将矩阵一行乘上一个常数 \(x\) 后加到另外一行上，行列式的值不变。根据上两条这个操作相当于加上一个行列式为零的行列式。

• 一个矩阵满足若 \(j<i\) 则 \(a_{i,j}=0\) ，即右上三角矩阵，则其行列式为主对角线元素乘积。因为不难发现只有一种贡献不为0的排列。

有最后一条性质，可以考虑用类似高斯消元的方式，每次将一行与其它行进行消元，以使一列变为零，最终得到右上三角矩阵。

于是我们有 \(O(n^3)\) 求解行列式的方法。

2.LGV引理

LGV引理的内容为，若存在有边权的有向无环图和两个不相交的大小均为 \(n\) 的点集 \(A\) 和 \(B\) ，构造矩阵 \(M\) 使 \(m_{i,j}\) 表示 \(A_i\) 到 \(B_j\) 的所有方案数边权乘积之和，则 \(M\) 的行列式 \(\det(M)\) 为

\[\sum_{p}(-1)^{\tau(p)}\prod_{i=1}^n m_{i,p_i}=\sum_{S:A->B}(-1)^{\tau(\sigma(S))}\omega(S) \]

其中 \(S\) 表示使 \(A\) 到 \(B\) 两两配对后每对由 \(A\) 到 \(B\) 产生 \(n\) 条路径并使 \(n\) 条路径互不相交的一种方案， \(\sigma(S)\) 表示配对方案的逆序对个数， \(\omega(S)\) 表示 \(n\) 条路径边权积的积。

所以等式左边相当于没有任何限制的将 \(A\) 与 \(B\) 配对后逆序对个数为偶数的贡献（贡献为所有路径边权乘积的乘积）减去逆序对个数为奇数的贡献，等式右边则相当于加入路径互不相交的限制。

所以左边比右边多出来的即为所有存在相交的路径方案的答案。如下图

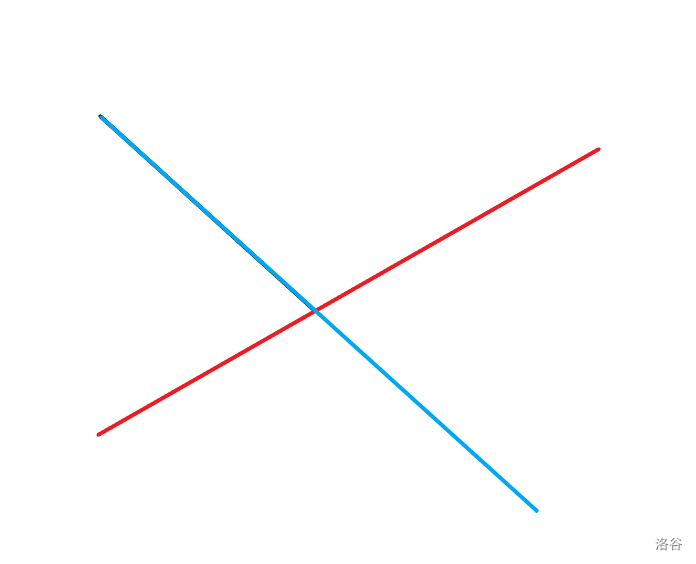
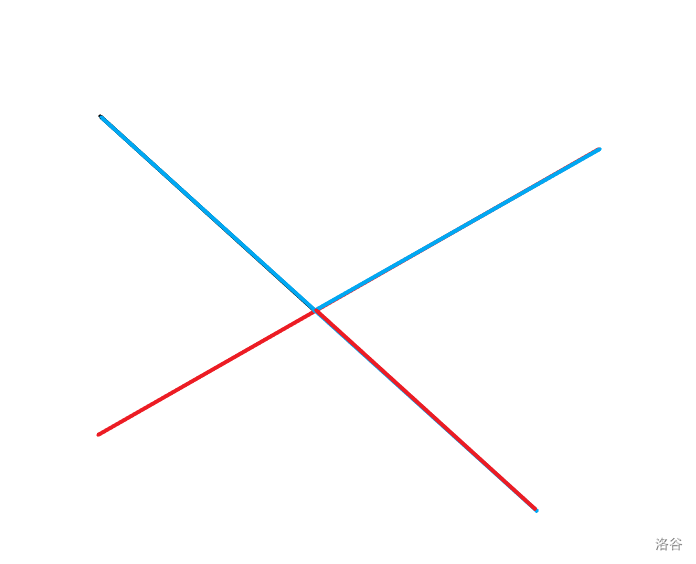
可以发现对于一种存在交点的情况，若选择一对存在交点的路径，将这两个路径的最后一个交点后的部分互换，可以得到一个新的存在相交的方案且贡献不变，而由于交换了一对配对则逆序对奇偶性改变。

若选择所有存在交点的路径对中路径编号最小的交换，则一种存在交点的逆序对为偶数的情况与一种逆序对为奇数的情况互相对应，于是它们的贡献相等，系数相反，总贡献为零，则左右相等。

有了这个定理，可以不用连通性关系来获得路径是否相交的信息。

3.矩阵树定理

定理内容是无向图的度数矩阵减去邻接矩阵，在去掉一行一列后的代数余子式为其生成树个数。首先度数矩阵减去邻接矩阵名为拉普拉斯矩阵，其形态如下：

\[L= \begin{bmatrix} d_1 &-1 &0 &\cdots&-1\\ -1 &d_2 &0 &\cdots&0\\ 0&0&d_3&\cdots&-1\\ \vdots&\vdots&\ddots&\ddots&\vdots\\ -1&0&-1&\cdots&d_n \end{bmatrix} \]

• 引理1：无向图的拉普拉斯矩阵行列式为 \(0\)

证明考虑每一行的行和都为 \(0\)，可以把每一行都加到最后一行则最后一行全为 \(0\)，新矩阵的行列式为 \(0\)，故而原矩阵的行列式也为 \(0\)。

• 引理2：拉普拉斯矩阵的代数余子式全相同

代数余子式的定义是去掉 \(i\) 行 \(j\) 列后矩阵的行列式乘 \((-1)^{i+1}\)，以下设 \(L'_{i,j}\) 为去掉第 \(i\) 行第 \(j\) 列后的矩阵。

由于矩阵转置后仍为原矩阵，只需要证明一行内任意两个代数余子式相同即可，进一步只需要 \(|L'_{1,1}|=(-1)^{1+i}|L'_{1,i}|\)。这样设第 \(i\) 列去掉第一行后的列向量为 \(c_i\)，把 \(L'_{1,i}\) 中除了第一列外都加到第一列，则第一列变为 \(-c_i\)，而此时矩阵列向量为 \(-c_i,c_1,c_2\dots c_{i-1},c_{i+1}\dots c_n\)，原矩阵列向量为 \(c_1,c_2\dots c_{i-1},c_i,c_{i+1}\dots c_n\)，可以通过 \(i-2\) 次交换两列操作使得两者相等，再经过一次取反操作，得到上面的式子。

于是只需要证明 \(|L'_{i,i}|\) 为生成树个数即可。

• 引理3：树的拉普拉斯矩阵去掉第 \(i\) 行第 \(i\) 列后行列式为 \(1\)

考虑给点重标号为拓扑序，这样在使用第 \(i\) 行进行高斯消元的时候它只有 \(L_{i,i}=1\) 以及一个 \(L_{i,j}=-1\)，可以归纳证明。首先叶子肯定满足此条件，而一个节点被其儿子消元时一定可以乘系数 \(-1\) 将 \(L_{u,son}\) 位置变为 \(0\)，同时 \(L_{u,u}\) 减去 \(1\)，其它位置不变，这样遍历完所有儿子后一个非根节点仅剩其与父亲的连边。删掉第 \(n\) 行与第 \(n\) 列，不考虑根则由上述结论可得对角线剩余元素为 \(1\)，行列式为 \(1\)，又由引理 \(2\) 可得删去任何一行和其对应列行列式都为 \(1\)。

然后定义关联矩阵 \(M\)，大小为 \(n\times m\)，\(M_{i,j}=1\) 当且仅当 \(i\) 是第 \(j\) 条边的端点之一。直接计算可得 \(L=MM^T\)。

这样 \(|L|\) 就等价于 \(|MM^T|\)。然后要求非方阵矩阵乘法的行列式，使用 Binet - Cauchy 定理：若 \(A\) 为 \(n\times m\) 的矩阵， \(B\) 为 \(m\times n\) 的矩阵，则有

\[|A\times B|=\sum_{1\leq k_1<k_2<k_3\dots<k_n\leq m} \det((A_{rk_1},A_{rk_2},\dots A_{rk_n})(B_{ck_1},B_{ck_2},\dots B_{ck_n})) \]

就是说在 \(A\) 中选 \(n\) 列，\(B\) 中选编号对应的 \(n\) 行，所有方案两个矩阵相乘之后得到的行列式的和即为 \(A\times B\) 的行列式。

证明构造 \((n+m)\times (n+m)\) 的分块矩阵 \(N\)。

\[\begin{aligned} |N|&=\begin{vmatrix} A&0\\ I_m&B \end{vmatrix}\\ &=\begin{vmatrix} 0&-AB\\ I_m&B \end{vmatrix}\\ &=(-1)^{n}\begin{vmatrix} 0&AB\\ I_m&B \end{vmatrix}\\ &=(-1)^{n+nm}\begin{vmatrix} AB&0\\ B&I_m \end{vmatrix}\\ &=(-1)^{n+nm}|AB| \end{aligned}\]

然后展开算 \(N\) 的行列式，前 \(n\) 行是必须要选 \(A\) 矩阵的，所以得到 \(\det(A_{rk_1},A_{rk_2},\dots A_{rk_n})\)，那么前 \(m\) 列除了这 \(n\) 个选了的，其余的必须选择 \(I\) 中的 \(1\)，而剩下的不能选 \(I\) 中的 \(1\)，必须选择 \(B\) 中剩下的行，不难发现取两次补集后为 \(A\) 所选行对应编号的列，即为 \(\det(B_{ck_1},B_{ck_2},\dots B_{ck_n})\)。可以画图理解：

\[\begin{vmatrix} a_{1,1}&a_{1,2}&a_{1,3}&\cdots&a_{1,m}&0&0&\cdots&0\\ a_{2,1}&a_{2,2}&a_{2,3}&\cdots&a_{2,m}&0&0&\cdots&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&0&0&\cdots&0\\ a_{n,1}&a_{n,2}&a_{n,3}&\cdots&a_{n,m}&0&0&\cdots&0\\ 1&0&0&\cdots&0&b_{1,1}&b_{1,2}&\dots&b_{1,n}\\ 0&1&0&\cdots&0&b_{2,1}&b_{2,2}&\dots&b_{2,n}\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\ddots&\vdots\\ 0&0&0&\cdots&1&b_{m,1}&b_{m,2}&\cdots&b_{m,n}\\ \end{vmatrix}\]

这样三部分之间产生的逆序对个数，可以在选择的每一个 \(I\) 中的 \(1\) 处统计贡献，第 \(i\) 列和它后面选择的 \(A\) 产生逆序对，又和它前面选择的 \(B\) 产生逆序对，所以一定会产生 \(n\) 个逆序对，总共 \(n(m-n)\) 个逆序对，于是系数为 \((-1)^{n+nm+n(m-n)=(-1)^{2nm}=1}\) 所以得证。

以上证明，学习自 知乎。

回到矩阵树定理，那么我们现在要求 \(L'_{i,i}\) 的行列式。

\[\begin{aligned} |L'{i,i}|&=\sum_{1\leq k_1<k_2<k_3\dots<k_{n-1}\leq m} \det((M'_{rk_1},M'_{rk_2},\dots M'_{rk_n})(M'^{T}_{ck_1},M'^{T}_{ck_2},\dots M'^{T}_{ck_n}))\\ &=\sum_{1\leq k_1<k_2<k_3\dots<k_{n-1}\leq m} \det((M'_{rk_1},M'_{rk_2},\dots M'_{rk_n})(M'_{rk_1},M'_{rk_2},\dots M'_{rk_n})^T)\\ &=\sum \det(L'') \end{aligned}\]

意思是由于 \(M\) 的定义，其选择 \(n-1\) 列的转置即是 \(M^T\) 选择对应 \(n-1\) 行所得结果，且选择后的矩阵相当于只保留了选择的 \(n-1\) 条边的子图的关联矩阵，所以得到 \(L''\) 是原图只保留 \(n-1\) 条边得到的拉普拉斯矩阵去掉第 \(i\) 行和第 \(j\) 列，由引理3，只有这些边构成树会产生 \(1\) 的贡献，不然由于其不联通一定可以行变换成若干拉普拉斯矩阵的分块矩阵，消掉一行一列后由引理2，贡献仍为 \(0\)。

于是得证。至于有向图情况不太会，OI-wiki 的证明也不太懂，那就先这样吧。

参考资料 矩阵树定理入土