回文子串划分-CF932G

就是求将字符串划分为若干回文子串的方案数。

1.回文后缀与border

首先，回文串的回文后缀集合与 border 集合完全相等，由回文串的定义可得。于是，border 的性质可以在回文后缀中使用，比如定理：将字符串的所有 border 的长度排序后，可以分割为 \(O(\log)\) 个等差数列子串。

证明如下：

• 对于字符串 \(s\) 的任何一个 border \(x\) ，定义 \(per(s,|s|-x)\) 为 \(s\) 的一个周期。则有长度为 \(y\) 的周期一定有 \(\forall i \in[1,|s|-y],s_i=s_{i+p}\) ，即为原串移动 \(y\) 之后仍可以和原串匹配。证明考虑由于存在长度为 \(x\) 的 border 即长度为 \(x\) 的前后缀能匹配，就相当于移动 \(|s|-x\) 之后进行匹配，于是定义与性质等价。

• 显然，对于一个字符串，所有小于 \(|s|/2\) 的周期的长度都是一个最短周期的倍数。但对于 \(aaaaabaaaa\) 这个字符串，存在周期 6,7,8,9 等，这种只能完整存在一次的周期不符合这个定理（由于倍数后的周期不能完整存在没有意义）。

• 对于字符串 \(s\) ，所有长度大于 \(|s|/2\) 的 border 长度构成等差数列。由于它们对应的周期的长度为最短周期的倍数，为公差为最短周期的等差数列，则它们的长度也为等差数列。

• 由上一条，将字符串 \(s\) 中所有大于 \(|s|/2\) 的 border 拿出，则它们构成一个等差数列。剩余的 border 均为最长的 border 的 border，可以递归处理且一次会将长度缩减一半。

于是字符串的 border 可以排序后分割为 \(O(\log)\) 个等差数列子串，回文串的回文后缀长度也可以排序后分割为 \(O(\log)\) 个等差数列子串。

2.优化DP

设 \(i\) 结尾的最长回文后缀长度为 \(x\) ，这个回文后缀的回文后缀长度集合为 \(S\) 。可列DP方程

\[f_i=\sum_{j\in S} f_{i-j} \]

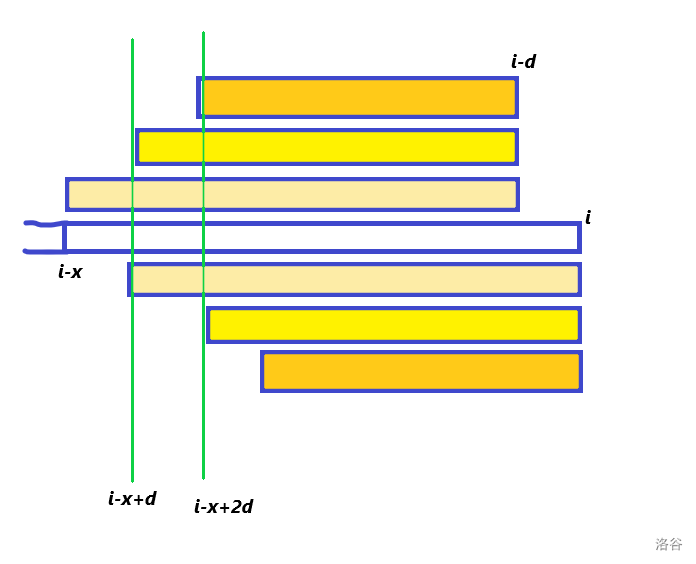
根据上面的结论，我们将 \(S\) 分为若干等差数列。观察对于 \(x\) ，设它所处的等差数列公差为 \(d\) ，则转移的来源 \(i-j\) 可以为 \(i-x,i-x+d,i-x+2d\dots\) ，我们发现当处理到位置 \(i-d\) 时，由于 border 前后缀相等，故也存在长度为 \(i-d\) 这个回文后缀，同样在公差为 \(d\) 的等差数列中转移来源也为 \(i-x,i-x-d,i-x-2d\dots\) ，只是项数减少了一项，如下图。

于是考虑建立回文自动机，每个节点记录 \(dif[i]=len[i]-len[fail[i]]\) 表示它和最长回文后缀的差值（即为周期，也就是公差），对于 \(i\) 到奇根的 fail 树上的链，记录 \(slink[i]\) 表示第一个 \(dis[slink[i]]!=dif[i]\) 的点。

于是，设插入第 \(i\) 个字符后最长回文后缀所在节点位 \(pos\) ，则只要不断跳 \(slink[pos]\) 即可得到每个等差数列的首项（或者说末项，为途中肉色部分），对每个节点 \(id\) 记录 \(g[id]\) 表示它上一次出现时（由于跳的是最小周期，上一次出现肯定为图中 \(i-x\) 处开始）它到 \(slink[id]\) 之间的 \(f\) 的和，即它所在等差数列的贡献即可。

3.code

模板题CF932G为求偶回文串划分，做法为将 \(g\) 分类为等差数列中长度为奇数的和长度为偶数的分别转移。

#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
int to[1000005][26],fail[1000005],dif[1000005],slink[1000005];
int len[1000005],cnt,r0,r1,last,n;
char ss[1000005],s[1000005];
void init()
{
	cnt=1;r0=0;r1=1;
	fail[r0]=r1;fail[r1]=r1;
	len[r0]=0;len[r1]=-1;last=r1;
}
void insert(int i,int c)
{
	int id=last;
	while(s[i]!=s[i-len[id]-1]) id=fail[id];
	if(!to[id][c])
	{
		len[++cnt]=len[id]+2;
		int pos=fail[id];
		while(s[i]!=s[i-len[pos]-1]) pos=fail[pos];
		fail[cnt]=to[pos][c];to[id][c]=cnt;
		dif[cnt]=len[cnt]-len[fail[cnt]];//更新dif和slink的值 
		slink[cnt]=(dif[cnt]==dif[fail[cnt]]?slink[fail[cnt]]:fail[cnt]);
	}
	last=to[id][c];
}
int f[1000005],g[1000005][2];
int main()
{
	scanf("%s",ss+1);n=strlen(ss+1);
	if(n&1){puts("0");return 0;}
	for(int i=1;i<=n/2;i++) s[(i-1)*2+1]=ss[i],s[i*2]=ss[n-i+1];
	init();f[0]=1;
	for(int i=1;i<=n;i++)
	{
		insert(i,s[i]-'a');
		for(int pos=last;pos>1;pos=slink[pos])
		{
			int l=len[slink[pos]]+dif[pos];//等差数列的末项定位，可以画图理解 
			g[pos][0]=g[pos][1]=0;
			g[pos][l&1]=f[i-l];
			if(fail[pos]!=slink[pos])
			{
				g[pos][1]=(g[pos][1]+g[fail[pos]][1^(dif[pos]&1)])%mod;
				g[pos][0]=(g[pos][0]+g[fail[pos]][0^(dif[pos]&1)])%mod;
			}
			f[i]=(f[i]+g[pos][0])%mod;
		}
	}
	cout<<f[n];
	return 0;
}