第 K 大自动机

1.第K大问题

给定 \(n\) 个集合，每个集合选择一个数，问所有方案中选择的数的和第K大的是多少，\(\sum |S|\leq 1e5,k\leq 1e5\) 。

考虑和最大的选择状态，一定是每个集合中选择最大的值，第二大的一定是将某个集合选择最大值改为选择次大值，不难发现对于每个状态后继状态都应该是把某集合选择的第 \(i\) 大改为第 \(i+1\) 大。

我们把每个状态向后继状态连边，从根（最大的状态）开始广搜，用堆代替队列，这样第 \(k\) 个出队的即为第 \(k\) 大的状态。如下图（i表示选择集合的第i大）

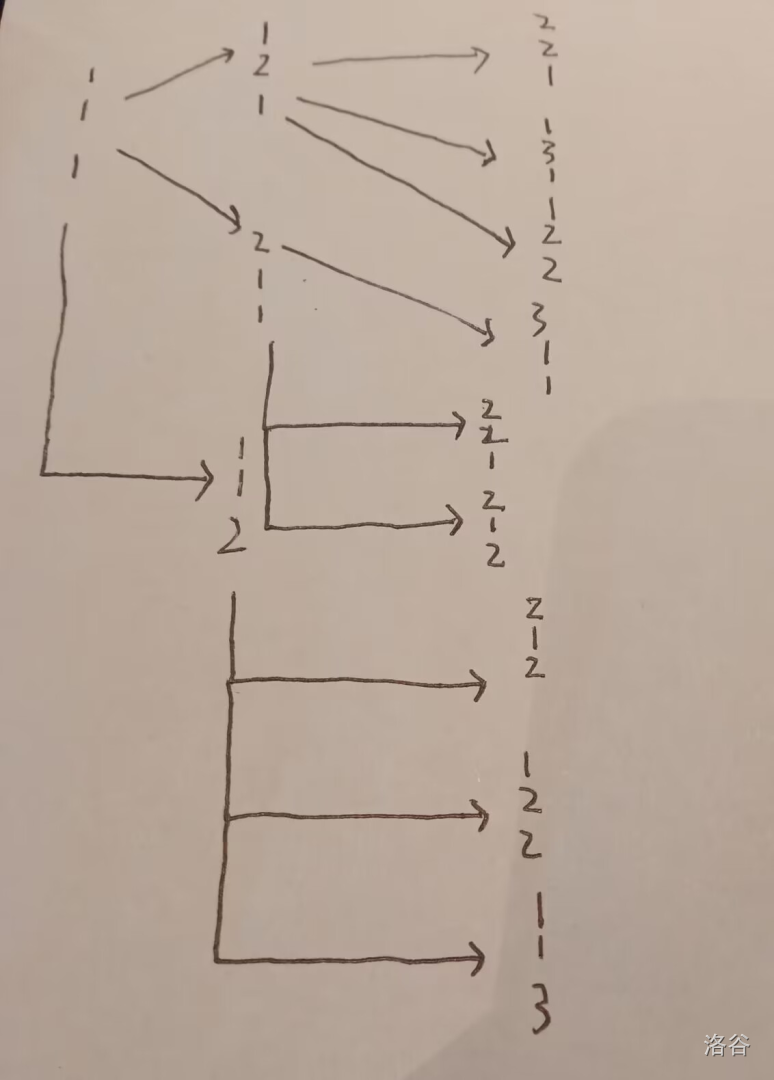
我们发现这时有重复，并且每个点的出度是 \(O(n)\) 级别的，这样时间复杂度实际为 \(O(n^2\log n)\) ，因为出队的点为 \(O(n)\) 级别而入队的点为 \(O(n^2)\) 级别。

2.优化

由于我们使用了堆，故而遍历原树的时候只需要保证最大值在堆中即可，考虑这个条件的充分条件，只要每个点的后继点都小于它（考虑反证如果最大值不在堆中则它的祖先没被遍历到过，与其为最大值矛盾）。

所以我们考虑状态 \(a_1,a_2,a_3\dots a_n\) 我们可以一个集合一个集合满足条件，由 \(1,1,1\dots 1\) ， \(2,1,1\dots 1\) ，\(3,1,1\dots 1\) 到 \(a_1,1,1\dots 1\) ，然后到 \(a_1,a_2,1\dots 1\) ，到 \(a_1,a_2,a_3\dots a_n\) ，这样每个状态的后继状态只有将当前位置增加和将下一个位置增加两个儿子，并且不会重复。

但是 \(a_1,a_2,a_3\dots a_{i-1},1,a_{i+1}\dots a_n\) 这个状态无法达到，因为在 \(a_{i-1}\) 到 \(a_i\) 这次转移中，已经将 \(a_i\) 加一，不可能再为 \(1\) ，我们可以进行反悔操作，若某状态中，一个位置选择了次大值，则它可以更换为最大值，之后将下一个位置增加。这样每个含有选择最大值的状态都可以通过反悔达到（因为一个后缀选取最大值会在没有改变这些位置的时候取到）。

然后有了反悔儿子又不一定小于父亲了。。。这种操作都是把 \(i-1\) 集合次大改为最大， \(i\) 集合最大改为次大，故而只要 \(i\) 集合最大值和次大值的差大于 \(i+1\) 集合最大值和次大值的差，排序即可。

于是我们建立了每个点最多三个出度的自动机，并且没有重复节点，完美解决了上述的问题。如图

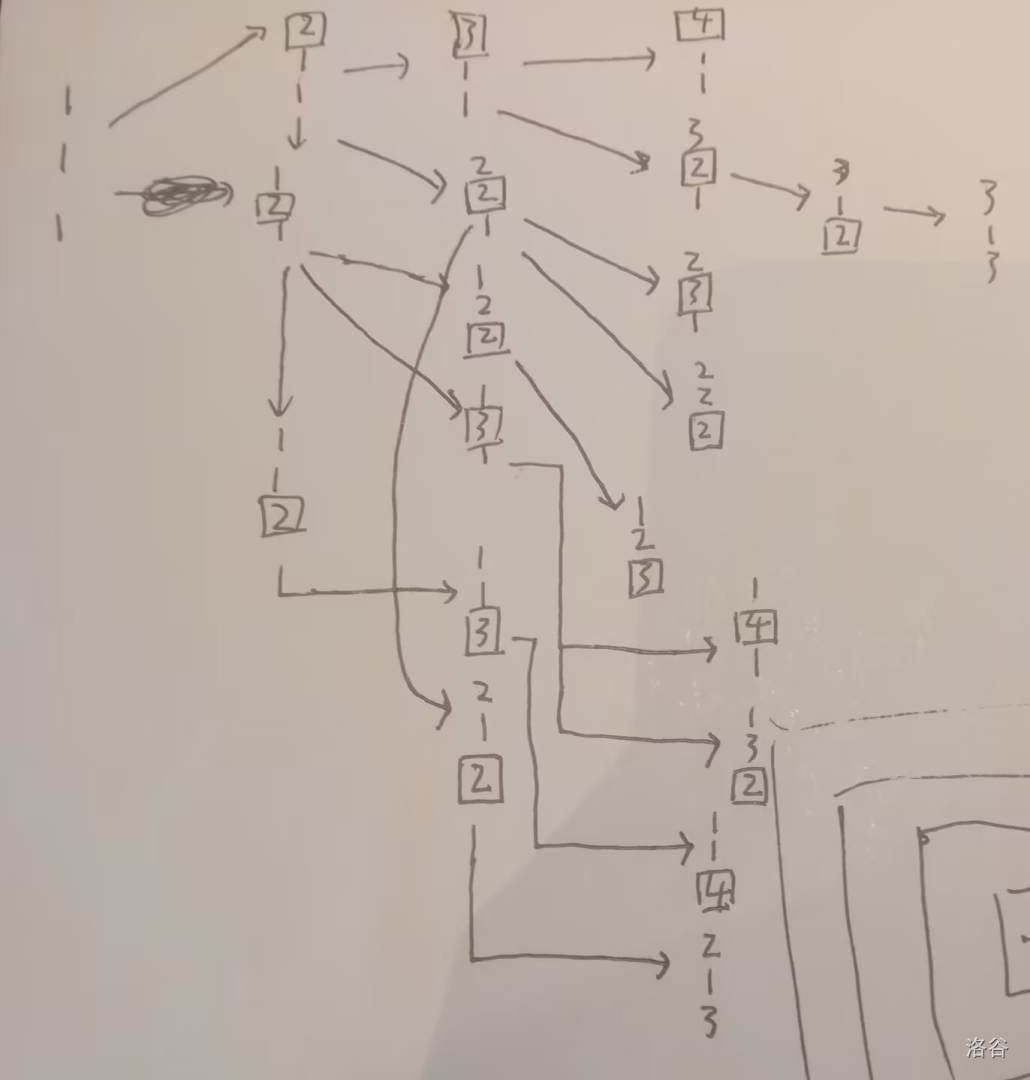
当时以为3 1 3不会出现还画出来了

3.例题

题目：[CCO202] Shopping Plans

把每个种类看做一个集合，只要求出每个种类选数第 \(i\) 大的方案这就是一个第K小问题，可以直接建第K小自动机。

然后每个集合互相独立，求选数第 \(i\) 大的方案，也是一个变式第K小问题，考虑最小状态一定是排序后选最左边的 \(x\) 个点，让一个状态和变大可以多选一个数或将一个数向右移动一位。和刚才一样，对于一个状态先把最后一个选的数移动到位，然后挪第二个，第三个。具体地，记录 \((x,y,z)\) 表示当前没挪的有 \(y\) ，已经挪完的最左边的是 \(z\)（即为 \(y\) 右边第一个），左边到 \(x\) 的前缀仍都选的状态。这样每个点可以移动 \(y\) ，还可以固定 \(y\) 并移动 \(x\) 。

对于多选一个数，钦定只在所有数为一个前缀时才加入，其实相当于枚举选多少个，总之复合出度小、无重复、每个点比父亲大、存在最小状态四点，就建立了第K小自动机。

具体实现上，把每个状态的当前位置和移动到的位置用结构体压在优先队列里即可。

4.code

#include<bits/stdc++.h>
using namespace std;
const long long inf=1e14;
struct s1
{
	int x,y,z;long long sum;
	friend bool operator <(s1 x,s1 y){return x.sum>y.sum;}
};//表示前x都选了，x之后第一个选的是y，第二个选的是z，即y可以挪到z 
struct s2
{
	int pos,now;long long sum;
	friend bool operator <(s2 x,s2 y){return x.sum>y.sum;}
};//表示上一次移动的点是pos，选取了a[pos]中第now小的值，pos之后的状态均取最小 
struct jgt
{
	int l,r;vector<long long>mi;//mi相当于记忆化 
	priority_queue<s1> q;vector<int>x;
	inline long long findans(int j)
	{//这个SB实现j必须严格不变或+1 
		if(j<mi.size()) return mi[j];
		if(q.empty()) {mi.push_back(inf);return mi[j];}//自动机里没有值 
		s1 u=q.top();q.pop();mi.push_back(u.sum);//多选一个，只在选取前缀时更新 
		if(u.z==x.size()&&u.y==u.x+1&&u.y+2<=r&&u.y+1<x.size()) q.push((s1){u.x+1,u.y+1,u.z,u.sum+x[u.y+1]});
		if(u.x>=0&&u.x+1<u.y) q.push((s1){u.x-1,u.x+1,u.y,u.sum-x[u.x]+x[u.x+1]});//将x移到x+1，y就变成了第二个 
		if(u.y>=0&&u.y+1<u.z) q.push((s1){u.x,u.y+1,u.z,u.sum-x[u.y]+x[u.y+1]});//将y移到y+1，注意不能超过z 
		return mi[j];
	}
}a[200005];//压缩状态后的自动机第一层必须先访问到小的节点，而之后的层由于原状态树的性质无需排序 
bool cmp(int x,int y){return a[x].findans(2)-a[x].findans(1)<a[y].findans(2)-a[y].findans(1);}
int top[200005];priority_queue<s2>q;
int main()
{
	int n,m,k,aa,bb;cin>>n>>m>>k;
	for(int i=1;i<=n;i++) scanf("%d%d",&aa,&bb),a[aa].x.push_back(bb);
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d",&a[i].l,&a[i].r);
		sort(a[i].x.begin(),a[i].x.end());
		if(a[i].l<=a[i].r&&a[i].x.size()>=a[i].l)
		{//如果没有合法的方案，则自动机为空 
			long long tmp=0;//初始状态是最小的 
			for(int j=0;j<min(a[i].l,(int)a[i].x.size());j++) tmp+=a[i].x[j];
			a[i].q.push((s1){a[i].l-2,a[i].l-1,a[i].x.size(),tmp});
		}
		a[i].mi.push_back(0);//占位，早知道从0开始 
		a[i].findans(1);a[i].findans(2);
	}
	for(int i=1;i<=m;i++) top[i]=i;
	sort(top+1,top+m+1,cmp);long long tmp=0;
	for(int i=1;i<=m;i++) tmp+=a[i].findans(1);
	q.push((s2){0,1,tmp});//注意初始状态不能挪下一个点 
	int t;for(t=1;t<=k;t++)
	{
		if(q.empty()) break;
		s2 u=q.top();q.pop();//用小根堆遍历自动机 
		if(u.sum>=inf) break;//某个种类取不到就会贡献为inf 
		printf("%lld\n",u.sum);//自动机上第t小的点，直接输出 
		if(u.pos!=0) q.push((s2){u.pos,u.now+1,u.sum-a[top[u.pos]].findans(u.now)+a[top[u.pos]].findans(u.now+1)});//now向后挪一格
		if(u.pos!=m) q.push((s2){u.pos+1,2,u.sum-a[top[u.pos+1]].findans(1)+a[top[u.pos+1]].findans(2)});//固定这个种类，移动下一个种类
		if(u.pos!=m&&u.now==2)//挪动这个种类为最小，移动下一个种类，因为pos变成现在的种类时必然挪动了，故没考虑过这种情况 
		q.push((s2){u.pos+1,2,u.sum-a[top[u.pos+1]].findans(1)+a[top[u.pos+1]].findans(2)-a[top[u.pos]].findans(2)+a[top[u.pos]].findans(1)});
	}
	for(int i=t;i<=k;i++) puts("-1");
	return 0;
}

虽然但是，除了板子没见过（