全局最小割

1、全局最小割

有正权无向图当中，若边集 \(C\) 使得 \(\{V,E\backslash C\}\) 不连通，则称 \(C\) 为原图的割，求原图的最小割。这个问题等价于将原图染色为两个点集，两端颜色不同的边的边权之和。

考虑我们可以在多项式复杂度内解决 \(S-T\) 最小割。事实上原图中的两点 \(s,t\) 在最终的最小割中要么颜色相反，要么颜色相同。若为前者，则求出的 \(S-T\) 最小割就是最终的最小割，若为后者，则最终的最小割中 \(s,t\) 的连边一定没有贡献，故而可以将 \(s,t\) 合并为一个点。

具体地，合并后的点到 \(i(i\ne s,i\ne t)\) 的边权为 \(w(s,i)\)与 \(w(t,i)\) 的和，因为若两点在同一集合，则最终两条边要么同时产生贡献，要么同时不产生贡献（没有边视作边权为0，看作完全图）

这样到图中只有一个点的时候，最小割必然为之前的 \(n-1\) 次割中的一个。每次随便指定两个点，用网络流求解 \(S-T\) 割可以达到 \(O(n^3m)\) 的复杂度，由于我们补成了完全图所以这差不多是 \(O(n^5)\) 的很不优。

2、MinimumCutPhase

由于我们只需要求任意 \(s,t\) 的最小割，故而考虑维护原图的一个割，使得它为一对 \(s,t\) 之间的最小割即可。定义初始为空的集合 \(A\)，定义函数

\[w(i)=\sum _{j\in A} dis(i,j) \]

每次将 \(w\) 最小的点加入集合 \(A\) ，则对于当前 \(A\) 集合的诱导子图，最后一个加入 \(A\) 的点 \(u\) 和倒数第二个加入的点 \(v\) 的最小割为 \(w(u)\) 。尝试证明（因为真没想到正向思考的方式）。

考虑 \(w(u)\) 肯定为原图的一个割，但是不知道是否存在更小的割，于是要证明 \(u,v\) 的最小割不小于 \(w(u)\) 。按照当前 \(u,v\) 的最小割将诱导子图当中的点黑白染色，大概长这样：

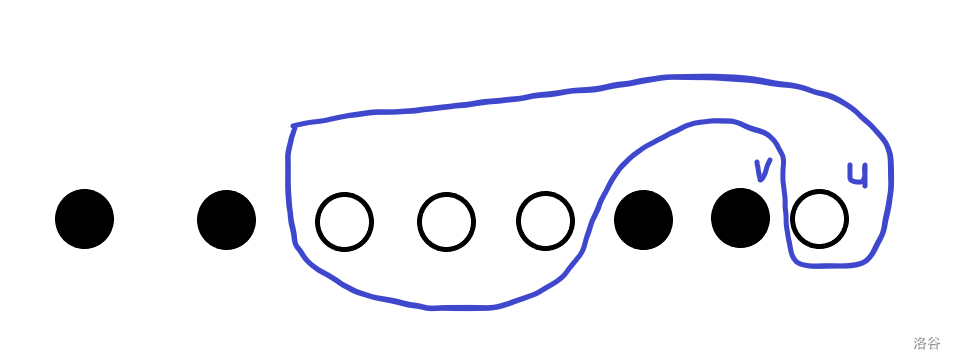
我们设第 \(i\) 个加入 \(A\) 的点为 \(A_i\) ，加入每个点 \(i\) 后黑白点之间两两的边权和 \(C_i\)。因为在加入第一个点时肯定有 \(C_1=w(1)\) ，故而考虑使用归纳法证明每个点都有 \(w(i)\leq C_i\)。我们称满足 \(A_i\) 和 \(A_{i-1}\) 颜色不同的 \(A_i\) 为关键点，那么 \(u\) 肯定为关键点，则只需要证明若上一个关键点 \(y\) 满足 \(w(y)\le C_y\) ，则当前关键点也满足即可。（以 \(y\) 为白色为例）

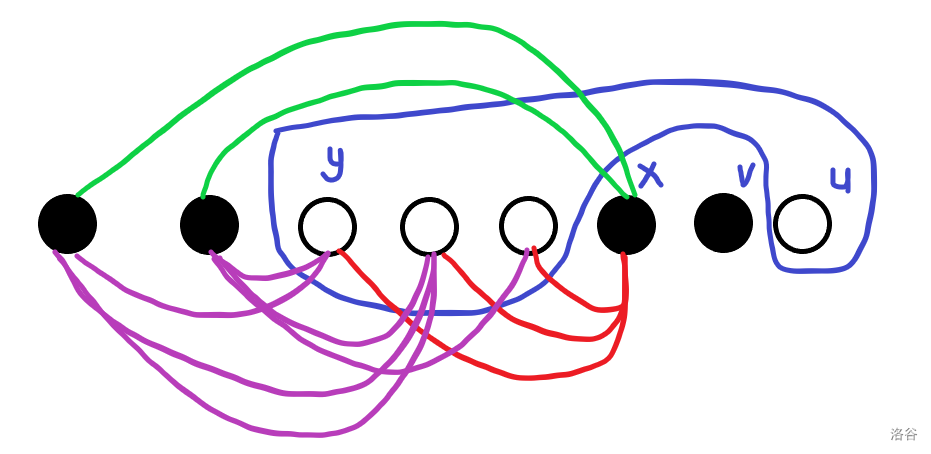
考虑 \(C_x\) 在 \(C_y\) 基础上增加了紫色和红色边，将将不等式 \(w(x)\le C_x\) 两边减去红色边，则要证明绿色边小于等于 \(C_y\) 加上紫色边，由于 \(y\) 先于 \(x\) 加入集合，故而绿色边权小于等于 \(w(y)\) ，由于 \(w(y)\le C_y\) ，则还有绿色边权和小于等于 \(C_y\) ，由于边权为正，故而等式右边加上紫色边仍然成立，则归纳得证。

于是可以在 \(O(n^2)\) 的复杂度内得到一个最小割，则全局最小割可以在 \(O(n^3)\) 的时间复杂度内完成。

3、code

#include<bits/stdc++.h>
using namespace std;
const int inf=1e9+7;
int w[605],z[605],a[605][605];
int c[605],v[605],s,t,n;
int SW(int num)
{
	for(int i=1;i<=n;i++) if(!v[i]) w[i]=0,c[i]=0;
	for(int i=1;i<=num;i++)
	{
		int id=0;
		for(int j=1;j<=n;j++) if(!v[j]&&!c[j]&&w[j]>w[id]) id=j;
		c[id]=1;z[i]=id;
		for(int j=1;j<=n;j++) if(!v[j]&&!c[j]) w[j]+=a[j][id];
	}
	s=z[num-1];t=z[num];
	//cout<<s<<" "<<t<<" "<<w[t]<<endl;
	return w[t];
}
int main()
{
	int m,aa,bb,cc,ans=inf;cin>>n>>m;w[0]=-1;
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d%d",&aa,&bb,&cc);
		a[aa][bb]+=cc;a[bb][aa]+=cc;
	}
	for(int i=1;n-i+1>=2;i++)
	{
		ans=min(ans,SW(n-i+1));v[t]=1;
		for(int j=1;j<=n;j++) if(!v[j])
		{
			a[s][j]+=a[t][j];
			a[j][s]+=a[j][t];
		}
	}
	cout<<ans;
	return 0;
}