从 Splay 开始的势能
此篇为不会分析LCT复杂度,忿忿而做。
势能分析
对于一个数据结构,若每次操作的复杂度和某个量相关,可以设它为势能函数 \(\phi\) 进行分析。
接着对于每一次操作 \(x\),设时间代价为 \(T_i\),势能变化量为 \(\Delta\phi_i\),令 \(A_i=T_i+\Delta\phi_i\),称 \(A\) 为摊还代价。这样把 \(m\) 次操作的上式求和,就有
这样如果确定 \(\sum_A\) 的极值就可以确定 \(\sum_T\) 的极值。一般做势能分析的时候,都选择势函数使得每个 \(A_i\) 在同一数量级,所以复杂度才是均摊的嘛。
比如花神游历各国这个题,势能线段树中设 \(\phi(i)\) 表示一个节点子树内节点需要被操作的最多次数,设全局 \(\phi\) 为每个节点 \(\phi(i)\) 的和。
设 \(t\) 表示每个数最多开根的次数,这样 \(\phi_0-\phi_m\) 最大值为 \(O(nt)\) 级别。
然后考虑每次操作的 \(A_i\) 即可。每次操作的时间代价分为两种:递归被完全覆盖的区间、递归未被完全覆盖的区间。后者每次对 \(A_i\) 的贡献为 \(O(\log n)\)。前者每递归一个节点 \(x\),会使该节点 \(\phi_i(x)\) 减小 \(1\),故而对 \(A_i\) 的贡献为 \(0\)。
于是每次操作的 \(A_i\) 都为 \(O(\log n)\),时间复杂度为 \(O(nt+m\log n)\)。
Splay
双旋的 Splay 是对的,单旋的 Splay 是错的。
对于 Splay 树的势能分析,设每个节点势能函数为 \(\phi(i)=\log si_i\),这样全局的势能函数最多为 \(O(n\log n)\),\(\phi_0-\phi_m\) 最大值为 \(O(n\log n)\)。
接下来考虑每次操作的 \(A_i\)。先考虑把一个点旋转到根的 Splay 操作,\(T_i\) 为旋转次数,不妨把每一次旋转拆开看,设第 \(j\) 次旋转的摊还代价为 \(A_{i,j}\)。
双旋一共有两种,zig-zig 和 zig-zag,分开考虑。
zig-zag 操作是我和父亲是不同向儿子时,连续旋转我两次。
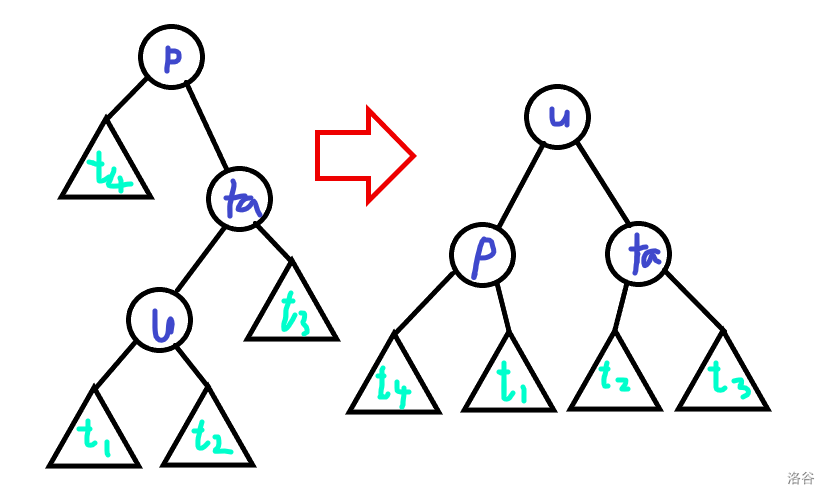
这次操作后只有 \(u,fa,p\) 三个节点子树大小改变,所以 \(A_{i,j}=2+\Delta\phi_{i,j}(u)+\Delta\phi_{i,j}(fa)+\Delta\phi_{i,j}(p)\)。
这样的式子不方便把每次旋转的 \(A_{i,j}\) 加和,考虑都化为和 \(u\) 相关的式子。可进行放缩求出 \(A_{i,j}\) 的上界,因为只需要上界。
首先把 \(\Delta\) 拆开。
\(A_{i,j}=2+\phi_{i,j}(u)-\phi_{i,j-1}(u)+\phi_{i,j}(fa)-\phi_{i,j-1}(fa)+\phi_{i,j}(p)-\phi_{i,j-1}(p)\)。
然后考虑 \(\phi_{i,j}(u)=\phi_{i,j-1}(p)\),因为两个子树一样大嘛。
\(A_{i,j}=2-\phi_{i,j-1}(u)+\phi_{i,j}(fa)-\phi_{i,j-1}(fa)+\phi_{i,j}(p)\)。
由于 \(u\) 是 \(fa\) 的儿子,\(\phi_{i,j-1}(fa)\geq\phi_{i,j-1}(u)\)。把右边的 \(-\phi_{i,j-1}(fa)\) 换成 \(\phi_{i,j-1}(u)\),式子的等号就会变为小于等于号,和期待的一样。
于是有 \(A_{i,j}=2-2\phi_{i,j-1}(u)+\phi_{i,j}(fa)+\phi_{i,j}(p)\),思考怎么把剩下的项去掉。发现 \(\phi_{i,j}(fa)\) 和 \(\phi_{i,j}(p)\) 的子树不交,于是有
所以式子变成了 \(A_{i,j}=-2\phi_{i,j-1}(u)+2\phi_{i,j}(u)\)。
zig-zig 操作是在我和我父亲是同向的儿子时,先旋转父亲,效果如下:
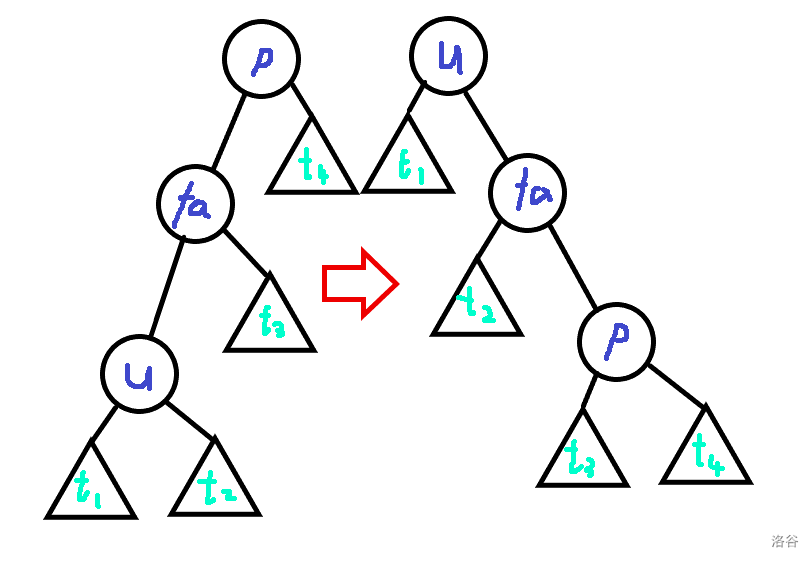
这次操作后也是只有 \(u,fa,p\) 三个节点子树大小改变,所以 \(A_{i,j}=2+\Delta\phi_{i,j}(u)+\Delta\phi_{i,j}(fa)+\Delta\phi_{i,j}(p)\)。
和 zig-zag 操作的分析同理,进行整理放缩。
\(A_{i,j}=2+\phi_{i,j}(u)-\phi_{i,j-1}(u)+\phi_{i,j}(fa)-\phi_{i,j-1}(fa)+\phi_{i,j}(p)-\phi_{i,j-1}(p)\)。
由于新的 \(u\) 和原来的 \(p\) 子树大小相同,故而 \(\phi_{i,j}(u)=\phi_{i,j-1}(p)\)。可得
\(A_{i,j}=2-\phi_{i,j-1}(u)+\phi_{i,j}(fa)-\phi_{i,j-1}(fa)+\phi_{i,j}(p)\)。
由于原来 \(u\) 是 \(fa\) 的儿子,\(\phi_{i,j-1}(u)\leq\phi_{_{i,j-1}}(fa)\)。可得
\(A_{i,j}\leq2-2\phi_{i,j-1}(u)+\phi_{i,j}(fa)+\phi_{i,j}(p)\)。
考虑像刚才一样用两个不想交子树的势函数和放缩把 \(2\) 去掉,在不等式左右同时加上 \(\phi_{i,j-1}(u)\)。有式子
所以可化为 \(A_{i,j}+\phi_{i,j-1}(u)\leq-2\phi_{i,j-1}(u)+\phi_{i,j}(fa)+\phi_{i,j}(u)\)。
然后 \(\phi_{i,j}(fa)\leq\phi_{i,j}(u)\)
所以有 \(A_{i,j}\leq 3(\phi_{i,j}(u)-\phi_{i,j-1}(u))\),也化成了只有 \(u\) 的形式。
这样每次要么 \(A_{i,j}\leq2(\phi_{i,j}(u)-\phi_{i,j-1}(u))\),要么 \(A_{i,j}\leq3(\phi_{i,j}(u)-\phi_{i,j-1}(u))\)。由于随着 \(j\) 的增大子树大小一直增大,不等号的右边为正,可以都放缩成 \(3(\phi_{i,j}(u)-\phi_{i,j-1}(u))\) 的形式。
然后 \(A_i\) 为所有 \(A_{i,j}\) 的和,正负抵消后为 \(\phi_{i,k}(u)-\phi_{i,0}(u)\),最多为 \(O(\log n)\) 级别。所以 \(\sum_A\) 为 \(m\log n\) 级别,可得只进行 splay 操作复杂度为 \(O(n\log n+m\log n)\)。
至于普通平衡树其它的操作,复杂度为访问节点的深度,这个值等于它旋转到根需要旋转的次数,所以访问后 Splay 其,即可保证复杂度。
Segment Beats
就是区间取 \(\min\),区间加,求区间和的操作,记录最大值、次大值,只有一次对 \(v\) 取 \(\min\) 满足 \(v\leq se\) 才递归求解。
这个感觉网上的分析也有挺多错解的,斗胆写一个。
如果设势能函数为 \(\phi(i)\) 表示 \(i\) 节点的颜色数,总势能 \(\phi=\sum \phi(i)\) 的话,每次暴力向左右递归都会至少使当前节点的势能减少 \(1\),但这个遇到区间加法操作可以直接让一个点的势能增加 \(O(n)\),直接错误。
一种可以正确分析的方式是设每个点的势能 \(\phi(i)\) 表示 \(i\) 节点的最大值是否与其父亲相同,是为 \(0\) 不是为 \(1\)。然后设总势能 \(\phi=\sum phi(i)dep(i)\),也就是线段树上所有满足条件节点的深度和。
这样每次暴力向左右递归的时候,子树里所有 \(\phi(i)=1\) 且 \(\max(i)=se\) 的点 \(i\) 的势能都会减小为 \(0\)。但是这样分析,可能一次递归中很多点指定的势能减小的点相同,用很多时间代价减少了较小的势能。考虑一个点只能被它到根的链上的点指定,而遍历它们的 \(T_i\) 为 \(O(\log dep(i))\) 级别,正好可以消除当前点的势能。
而非暴力递归涉及一次 \(pushup\) 操作,可能会使 \(\phi(i)\) 变为 \(1\),最多增加 \(O(\log^2 n)\) 的势能,区间加操作同理,打懒标记的点势能不变。所以每次操作首先 \(T=O(\log n),\Delta\phi=O(\log^2 n)\),之后每增加一个 \(T\) 就会减小 \(\phi\),并且每次减小 \(\phi\) 消耗的 \(T\leq -\Delta\phi\),所以每次 \(A_i\) 在 \(O(\log^2 n)\) 级别。
那如此分析,为什么区间取 \(\max\) 也是对的?
可以再设置表示最小值和次小值是否相同的 \(\phi'\),这样一次取 \(\min\) 操作在非暴力递归的时候最多增加 \(O(\log^2 n)\) 的 \(\phi'\),暴力递归只会减少 \(\phi'\),故正确。
其它均摊数据结构
线段树合并也可以势能分析证明均摊复杂度。设势能函数为 \(\phi\) 等于所有线段树上的节点总数,这样每次运行 merge(x,y) 函数的时候两个位置都有点,而只会返回一个。所以每次运行使 \(T\) 加一,就会使 \(\phi\) 减一,\(A\) 为 \(0\)。复杂度为 \(\phi_0-\phi_m=O(n\log n)\)。
一个启示是不能把一棵动态开点线段树多次合并到别的地方,即使可持久化也不行。原因就是付出了时间代价而势能没有减小。
LCT也是势能来的。设势能函数 \(\phi\) 为满足一个点 \(u\) 到其重儿子 \(v\) 的边为虚边的点数。这样 \(\phi_0-\phi_m\) 为 \(O(n)\) 级别。
每次 access 的时候的 \(A_i\)。每次会跳一个点到根的所有虚边,其中不是刚刚所说的连向重儿子的虚边最多为 \(O(\log n)\) 级别,会使 \(T\) 加一,并且可能断掉连向重儿子的实边,使 \(\phi\) 加一。而跳连向重儿子的虚边,会使虚边变为实边,并且不会断掉连向重儿子的实边,会使 \(\phi\) 减一,所以 \(A_i\leq O(\log n)+O(\log n)\)。所以总复杂度为 \(O(m\log n)\)。
但是你每次 access 的复杂度不是 \(O(1)\) 啊!然后我就想是不是所有 Splay 中某个势能函数能保证复杂度,但是尝试了几个都不对。
可见我还是不会势能分析,但是至少不能犯用线段树和并求区间数颜色的错误了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号