题解-2025暑假集训模拟赛3-体测

【题目描述】

一学期一度的体测开始了。

小明所在年级有若干名学生，他们希望在某个时间段内进行某个项目的体验。

一共有 $n$ 个需求，第 $i$ 个需求是在第 $l_i$ 天到第 $r_i$ 天进行第 $a_i$ 个项目的体测。

为了公平，一个项目一天只有有一名学生参加，但一天可以有举办多个项目。

校方很重视学生的要求，他们希望满足所有学生的要求，但他们也希望尽量减少需要体测的天数。

现在请小明求出最少需要体测的天数；如果无法满足，则输出“Sorry”。

【输入格式】

第一行一个整数$n$，表示需求数

接下来 $n$ 行，每行三个整数 $ l_i,r_i,a_i$

【输出格式】

一个整数或者“Sorry”

【样例 $1$ 输入】

【样例 $1$ 输出】

样例解释：选择天数为2,3,4,第一位同学在第2天测试项目2，第二位同学在第2天测试项目1，第三位同学在第4天测试项目2，第四位同学在第3天测试项目1，第五位同学在第4天测试项目1.

【样例 $2$ 输入】

【样例 $2$ 输出】

Sorry

【数据范围】

对于$30\%$的数据，$1\le n\le 6,l_i\le r_i\le 10$

另外对于$20\%$的数据，$a_i=1$

对于$100\%$的数据，$1\le n\le 10^5,a_i\le 10^9,l_i\le r_i\le 10^9$

部分分解法

其实我觉得这个题只给 $a_i=1$ 还是挺狡猾的，正解应该算是 $a_i=1$ 和 $a_i$ 全不同两个贪心拼起来。

$a_i=1$ 的情况，可以扫描天数，发现右端点就表示这个区间需要覆盖；每天选目前左端点最大，最迫在眉睫的区间覆盖；如果遇到没覆盖的区间左端点就表示没法覆盖。

以上直观说法，理性证明只需要知道“如果按这个做法没填上，一定填不上”。

考虑我们没填上的区间可以被天 $i$ 覆盖，那一定是先把这一天选 $i$，再调整选 $i$ 天的区间，直到调整直到调到空余的天，由于每个点可能调整到的位置一定在它的范围内，并且一个需要调整的 $i\in(l_i,r_i)$，新的 $i\in(l_j,r_j)$ 由于优先于 $i$ 选这个点，肯定有 $l_j\ge l_i$，也就是说每一次调整并不会使 $l_i$ 变大。所以调整到的位置一定在最开始的 $l_i$ 右侧。考虑右侧第一个空余位置，假设由 $(l_j,r_j)$ 调整到，那么它怎么可能在有空余的时候在没空余的部分，也就是左侧选呢？故矛盾。故不存在能调整到的右侧空余位置，也就是说一定填不上。

然后是 $a_i$ 全不同的情况，这个是最经典的贪心，按右端点排序后，从前到后每个尚未被覆盖的覆盖在右端点即可。考虑后面的区间 $r_j\ge r_i\ge pos$ 也就是说只需要比较 $l_j\le pos$，这样 $pos=r_i$ 时最大比较好。

理性证明可以通过问题转化：首先，如果一个区间完全包含另一个区间，则它没有用处。排除这样的区间，其实按右端点排序后左端点也不降。所以每一天产生作用的区间其实是排序后的一段区间，并且 $r_i$ 覆盖的区间的区间从 $i$ 开始。如此，就是每一个右端点可以覆盖从它开始的一部分点，问怎么覆盖，就一定遇到没覆盖的右端点就选即可。那么，加上没有用的点的话，它们放在那些被它们包含的区间后肯定被覆盖过了嘛，所以没有影响。

正解解法

首先按照 $a_i=1$ 的情况把右端点缩紧。因为我们后面的调整无非是想让各个颜色所选的点重合嘛，而右边被锁住的点应该已经有别的区间选了，我去选也没有意义。

然后应用 $a_i$ 全不同的方法贪心。具体来说就是按右端点排序，从前到后选右端点。选了之后能覆盖什么？事实上只要有重合区间的都能覆盖，因为刚才是从右向左限制了所有右端点都是可选的，或者说所有右端点两两不同，也就是说不管右端点小的区间怎么选，都不影响后面的区间仍有右端点可以选。也就是说随便取一个别的颜色的区间来，调整到在这一天体测都没问题。

那我们就面临抉择，选哪一个。首先随着所选的 $pos$ 增加，不再能被覆盖的区间肯定是右端点最小的；其次在后面我们选点时，也是右端点越小的越不具有覆盖能力。也就是说，留下右端点小的肯定不优。

但是要理性证明的话，就要面临“如果我匹配了一个区间，那它就不能匹配后面的了”这个问题，其实就是贪心后效性太强。这个在文章最后说。

诶这个时候我们发现，比如说这种情况

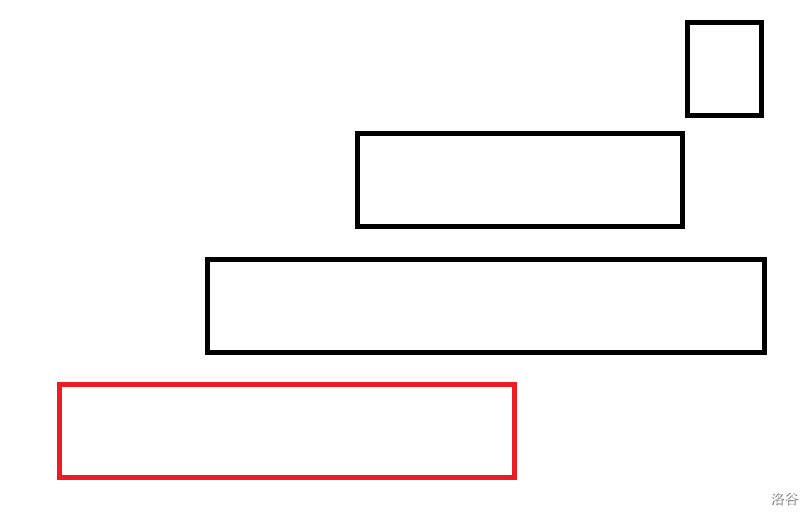
难道不会由于第二个区间被覆盖，而使第三个区间的右端点可以右移吗？但是事实上我们选取的右端点是从小到大的，也就是说上面这个例子，我们其实会先选第三个区间。既然从小开始选又怎么可能会出现需要右移的情况呢？

所以我们说明了“覆盖一个区间不会对后面的同颜色区间产生影响”。

代码

// ubsan: undefined
// accoders
#include<bits/stdc++.h>
using namespace std;
struct jgt{int l,r,typ,id;}a[100005],b[100005];
bool cmp(jgt x,jgt y){return x.r>y.r;}
bool cmp1(jgt x,jgt y){return x.r<y.r;}
bool cmp2(jgt x,jgt y){return x.l<y.l;}
priority_queue<pair<int,int> >st[100005];
vector<jgt>vec[100005];
set<int>col;
map<int,int>mp;
int tag[100005];
int main()
{
	freopen("sport.in","r",stdin);
	freopen("sport.out","w",stdout);
	int n,num=0;cin>>n;
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",&a[i].l,&a[i].r);
		scanf("%d",&a[i].typ);
		if(!mp[a[i].typ]) mp[a[i].typ]=++num;
		a[i].typ=mp[a[i].typ];
		a[i].id=i;
		vec[a[i].typ].push_back(a[i]);
	}
	for(int i=1;i<=num;i++)
	{
		sort(vec[i].begin(),vec[i].end(),cmp);
		priority_queue<pair<int,int> >q;
		vec[i].push_back((jgt){0,0,0,0});
		for(int j=0;j<vec[i].size()-1;j++)
		{
			q.push(make_pair(vec[i][j].l,vec[i][j].id));
			for(int k=vec[i][j].r;k>vec[i][j+1].r;k--)
			{
				if(q.empty()) break;
				//cout<<i<<" "<<j<<"has"<<k<<endl;
				int val=q.top().first;
				if(k<val) {puts("Sorry");exit(0);}
				int id=q.top().second;q.pop();
				a[id].r=k;
			}
		}
		if(!q.empty())
		{puts("Sorry");exit(0);}
	}
	for(int i=1;i<=n;i++) b[i]=a[i];
	//cout<<a[i].l<<" "<<a[i].r<<endl;
	sort(a+1,a+n+1,cmp1);sort(b+1,b+n+1,cmp2);
	int ans=0,pos=1;
	for(int i=1;i<=n;i++)
	{
		if(tag[a[i].id]) continue;
		ans++;tag[a[i].id]=1;
		//cout<<"build:"<<a[i].id<<endl;
		while(pos<=n&&b[pos].l<=a[i].r)
		{
			if(!tag[b[pos].id])
			st[b[pos].typ].push(make_pair(-b[pos].r,b[pos].id)),
			//cout<<i<<"ins"<<b[pos].typ<<" "<<b[pos].id<<endl,
			col.insert(b[pos].typ);
			pos++;
		}
		vector<int>tmp;
		set<int>::iterator it;
		for(it=col.begin();it!=col.end();it++)
		{
			int id=*it;
			if(id==a[i].typ) continue;
			//cout<<"OHHHHHH"<<a[i].id<<endl;
			while(!st[id].empty()&&-st[id].top().first<a[i].r) st[id].pop();
			if(!st[id].empty()) tag[st[id].top().second]=1,st[id].pop();
			if(st[id].empty()) tmp.push_back(id);
		}
		for(int k=0;k<tmp.size();k++)
		col.erase(col.find(tmp[k]));
	}
	cout<<ans;
	return 0;
}

反思

后来一想，这个题可能和 $a_i$ 全不同关系不大。感觉更像是有 $n$ 个区间，两个有重合的区间可以匹配，问最多成多少对。

这个问题显然是按右端点排序，匹配相邻的。原因是设当前区间集合为 $S$，那么不进行匹配得到的 $S-i$ 最多匹配 $x$ 对的话，匹配一次得到的 $S-i-j$ 只少了一个元素，也至少最多匹配 $x-1$ 对，所以肯定要匹配。

而匹配右端点最小的是因为剩下的右端点更大的区间 $k$ 需要比较 $l_j\le r_i$，所以剩下的 $r_i$ 越大越好。注意这里的证明是没有后效性的，因为它说明了剩下的集合最优。

然后如果有颜色的话是差不多的情况嘛，毕竟原本一些区间在一个点重合，去掉一个区间剩下的仍能重合。

所以如果按“选那个在剩下的里面不容易匹配的”而不是“选那个很快就没法匹配”思考的话，这个解法还是相当合理的（迫真

posted @ 2025-07-24 21:01 cinccout 阅读(42) 评论(0) 收藏举报

刷新页面返回顶部

cinccout的博客

题解-2025暑假集训模拟赛3-体测

【题目描述】

【输入格式】

【输出格式】

【样例 \(1\) 输入】

【样例 \(1\) 输出】

【样例 \(2\) 输入】

【样例 \(2\) 输出】

【数据范围】

部分分解法

正解解法

代码

反思

公告