MCM_算法篇

Cellular Automata
参考文章:
-
这篇文章将CA的实现给出,具体实现细节可以看:
Python 实现基于元胞自动机的生命游戏
澳洲变燠洲,考拉成烤拉!澳大利亚山火为什么难以控制?
贝叶斯定理/推断的运用
决策树/随机森林
YouTube: StatQuest with Josh Starmer
简单来说就是根据已有数据的feature和label,预测分类未知feature的label
我都用神经网络了,我学这个干啥
ROC And AUC
Sensitivity and Specificity
参考视频:Machine Learning Fundamentals: Sensitivity and Specificity
Sensitivity 和 Specificity 的作用是判别分类好坏的指标,能够帮助我们分辨使用那种模型来进行预测更好
当我们更看重正面时,用Sensitivity值更高的
当我们更看重负面时,用Specificity值更高的
其中Sensitivity表示成功预测正面的概率
Specificity表示成功预测负面的概率
他们都是通过混淆矩阵计算出来的,混淆矩阵,看下图:
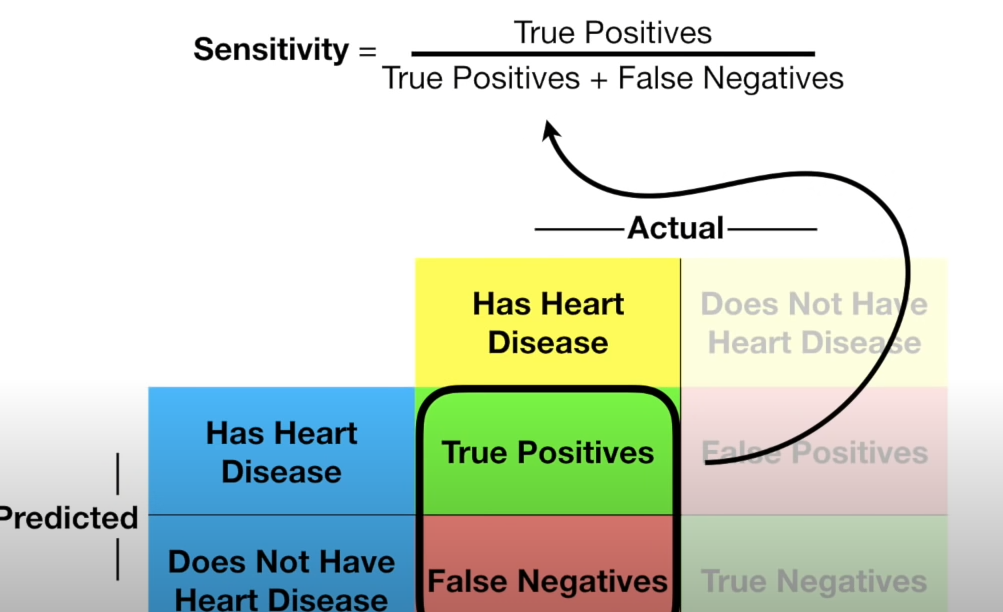
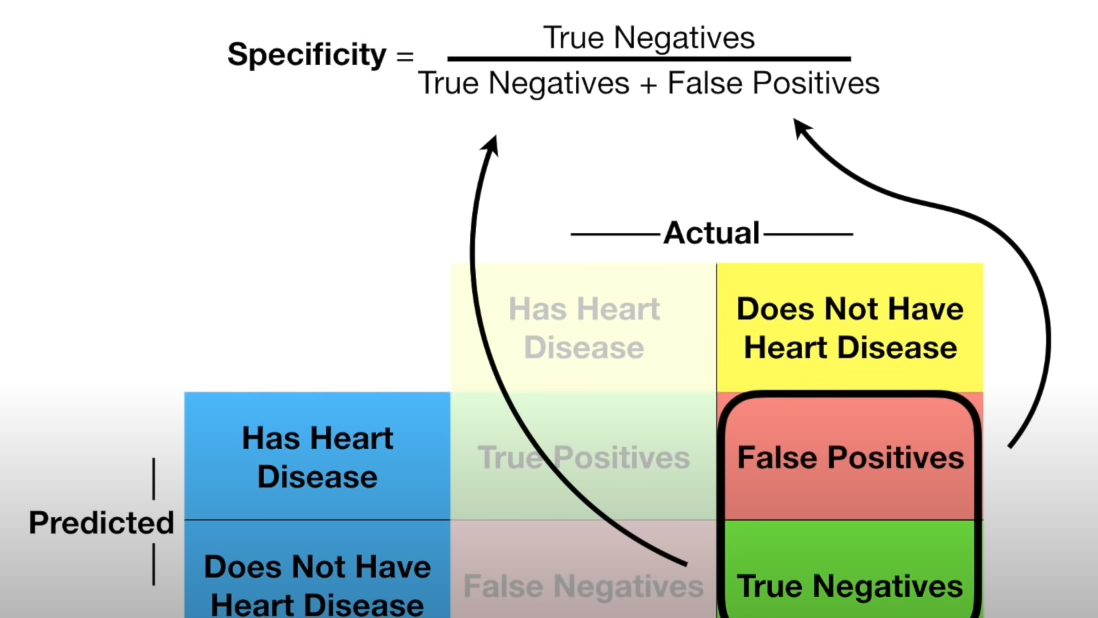
ROC (Receiver Operator Characteristic), AUC(Area Under Curve)/AUROC(Area Under ROC)
参考视频:ROC and AUC, Clearly Explained!
ROC 是根据不同分类阈值(如一个分类我将概率>0.5的记作正面,反之记作负面;当然我也可以>0.1的记作正面,反之记作负面; 0.5,0.1这些就是不同分类阈值)得到不同的混淆矩阵
从而计算出不同的Sensitivity和Specificity值,并在横纵轴都是0~1的二维图上绘制出来的曲线图
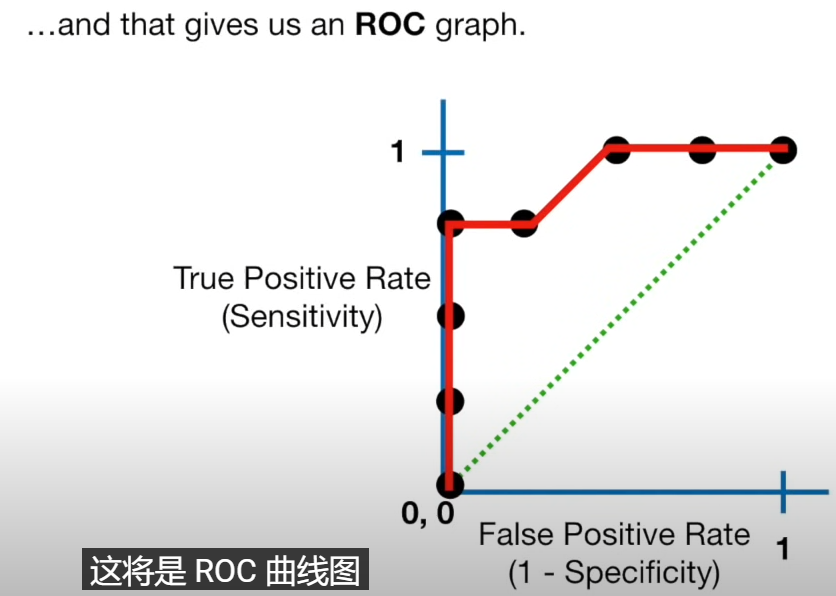
Sensivity越大,1-Specificity越小,表示这个分类阈值设置的越好,即分类效果越好
在穷举全部的分类阈值后,得到的ROC曲线,能够反应出这个模型分类效果的好坏
评价这个的标准是:AUC/AUROC
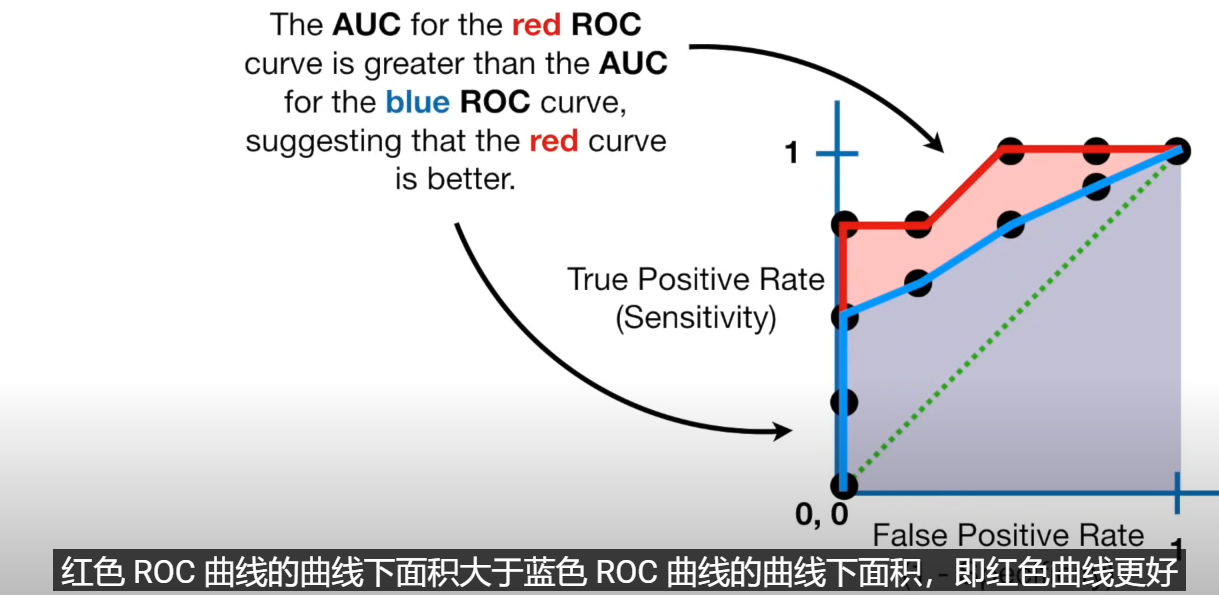
AUC score 就是这个面积的大小,其作用是评判模型分类的好坏,并可以为使用哪个模型做出选择
置信度和置信区间
参考视频:Confidence Intervals can be confusing, but with bootstrapping, they are a piece of cake. BAM!
对于许多样本数据,我们是不知道这些数据的真正的均值的(因为我们不可能搜集的到全部的数据,我们只有样本)
但是我们可以猜
对于每一批样本数据,我们取均值
当然,每一次得到的均值可能会不同
当我们取了许多批数据后,我们就可以得到均值的分布,如下:
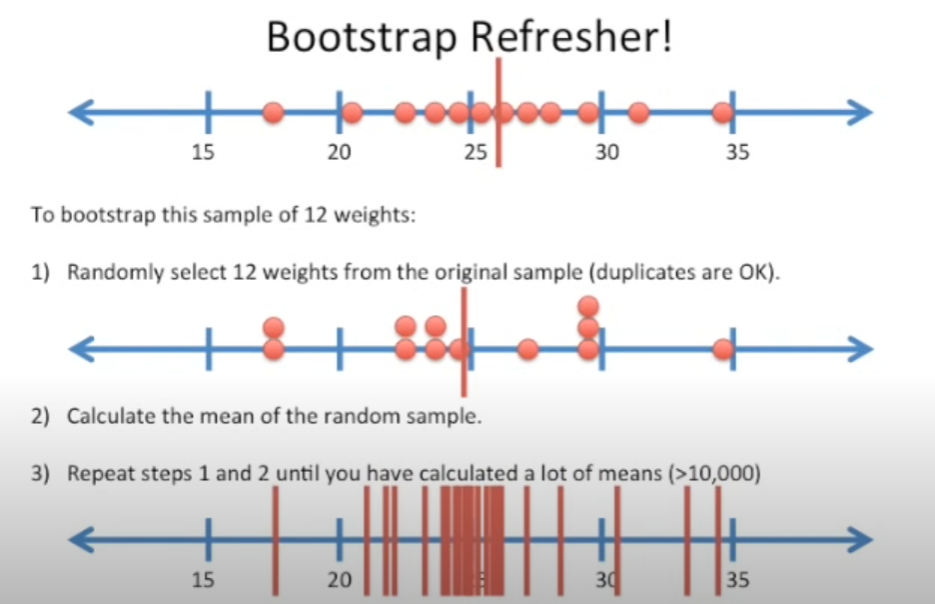
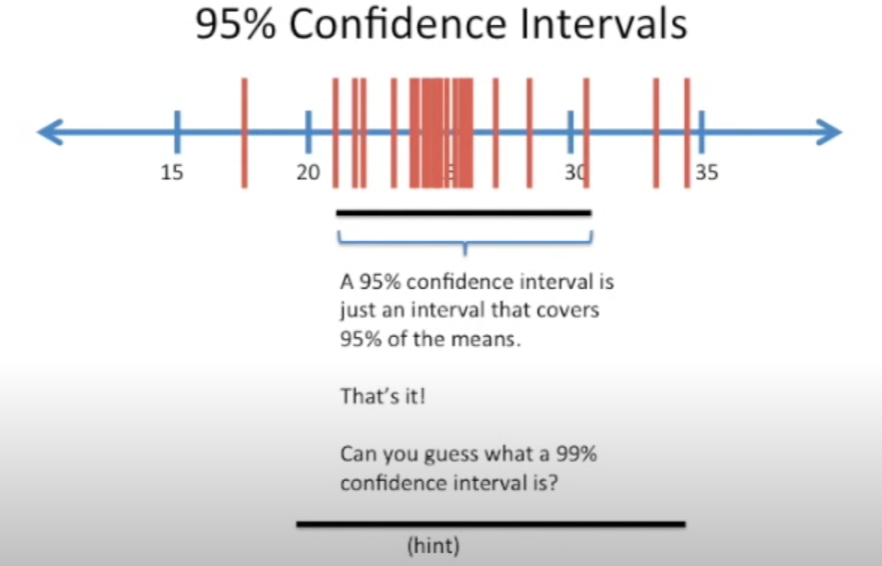
所谓的置信度和置信区间是捆绑在一起的,即置信度是对真正的均值在这个区间中的概率(也可以说有 置信度% 的均值都在这个区间中)
置信区间是 就是个区间而已
马尔科夫链
参考视频: Markov Chains Clearly Explained! Part - 1
马尔科夫链 即下一个状态只取决于当前的状态
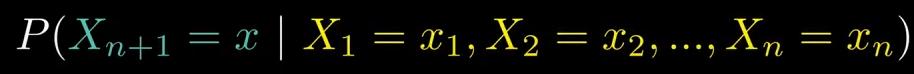
|
|
|
v
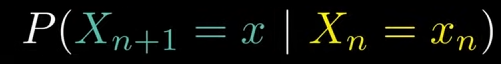
说起状态的转换我们就会想起:状态转换图
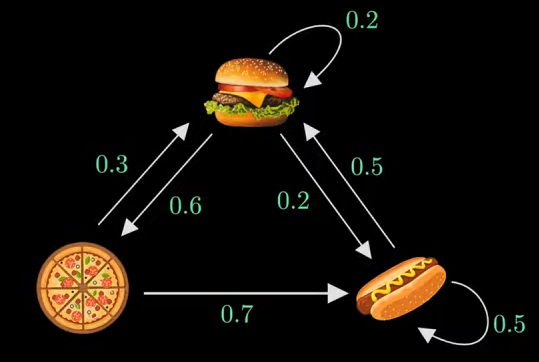
上述图表示如:假设今天我吃的是汉堡,那么明天我继续吃汉堡的概率是0.2,吃披萨的概率是0.6,吃热狗的概率是0.2
当然根据概率 P ( Tomorrow汉堡 | Today汉堡)+ P( Tomorrow披萨 | Today汉堡 )+ P( Tomorrow热狗 | Today汉堡 ) = 1
当我们将上述图转换成矩阵:

|
|
|
v
再给出当前状态π

相乘
|
|
|
v

就得到了下一个状态发生的概率
我们重复这个过程
|
|
|
v

进行许多次,最终π会收敛在一个不变的数值

pytorch编程结果:
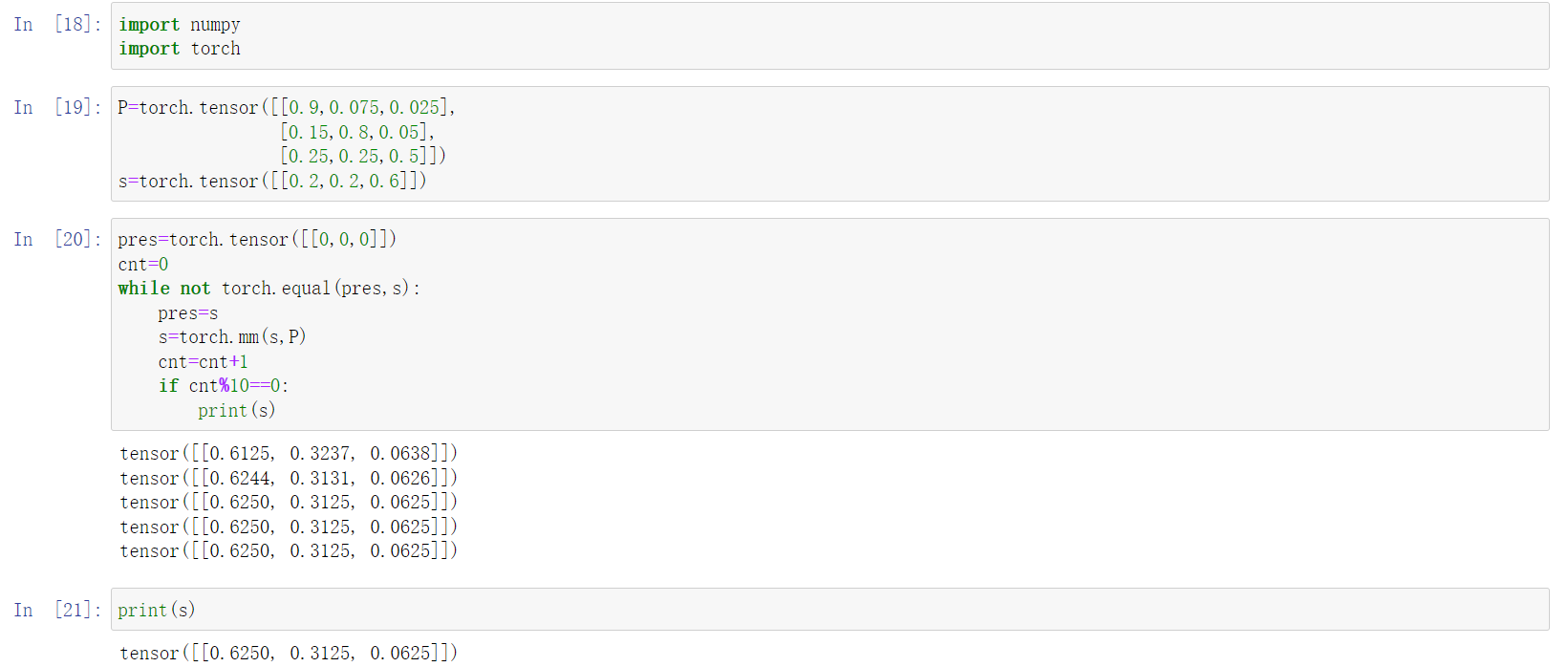
上述我们初始化矩阵为P,初始状态为s
然后最终收敛
概率统计基本知识
R^2
参考视频:R-squared, Clearly Explained!!!
R2的作用是用来评估两个变量之间的相关性大小,R2越大表示相关越强
R^2的值位于0~1之间
其计算方法如下:
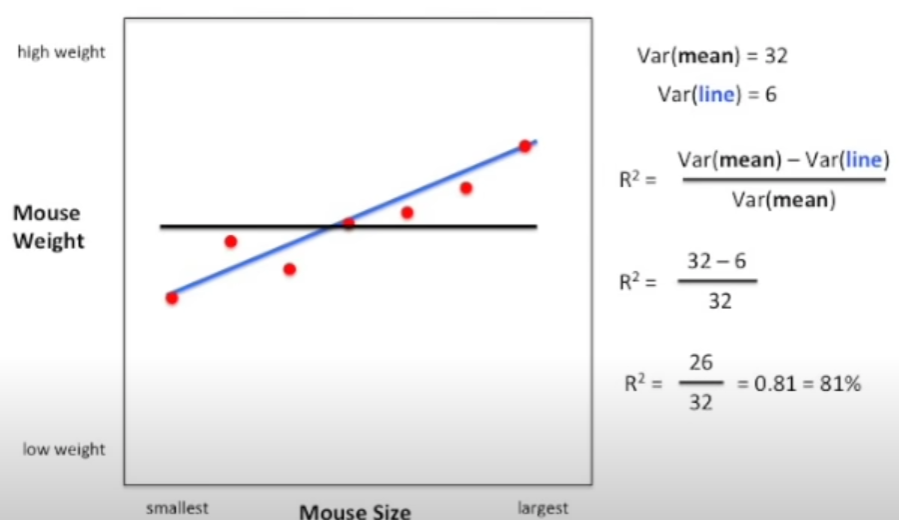
Var(mean)=∑(mean值-变量值)^2
Var(line)=∑(line上值-变量值)^2
这里计算的R^2=81% 表示 这两个变量的相关性 解释了 81% 的数据的变化
p值
参考视频:p-values: What they are and how to interpret them
p值是 量化 两种事务确实存在差异的 置信度
p值位于0~1之间
p值越小,表示越确信两者存在差异
那么问题来了,p值到底要多小,我们才能相信两者存在差异呢?
这里有一个阈值0.05,当p值<0.05时,表示我们有95%的置信度认为两者存在差异


 浙公网安备 33010602011771号
浙公网安备 33010602011771号