动手学深度学习_2预备知识

image

Memories in a Box-BigRicePiano

基础线性代数

image

声明：资料来自3Blue1Brown

什么是张成空间？

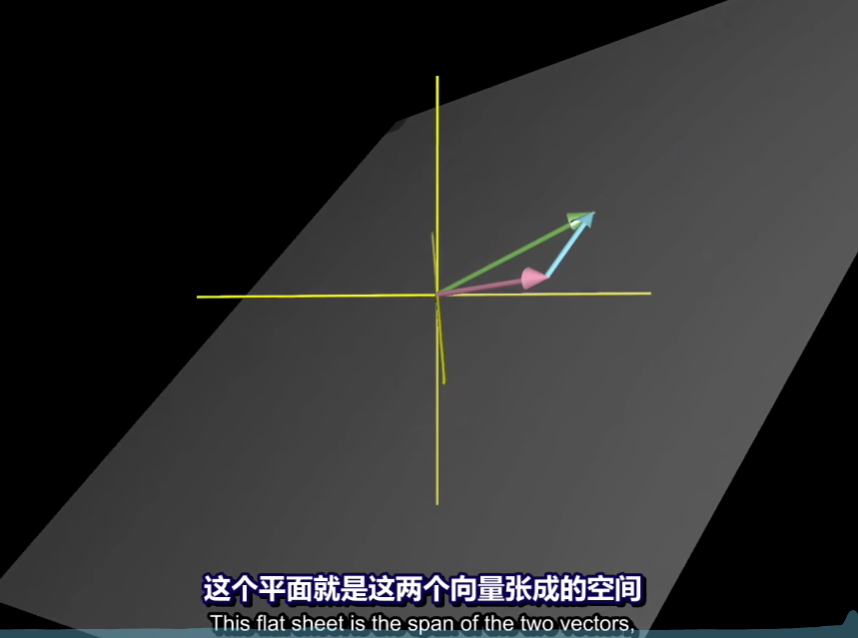
image

标量是用来伸缩向量的
向量可以看做一个空间上从“原点”到目的点的箭头，当我们不考虑箭头时，我们就可以将向量看成点
由于标量的不断变化，由基向量组成的新向量的集合就是张成空间

image
image
image

那么我们说这些向量是线性相关的，否则我们称其为线性无关

image

如何理解矩阵与线性变换？

我们首先需要了解一下空间变换
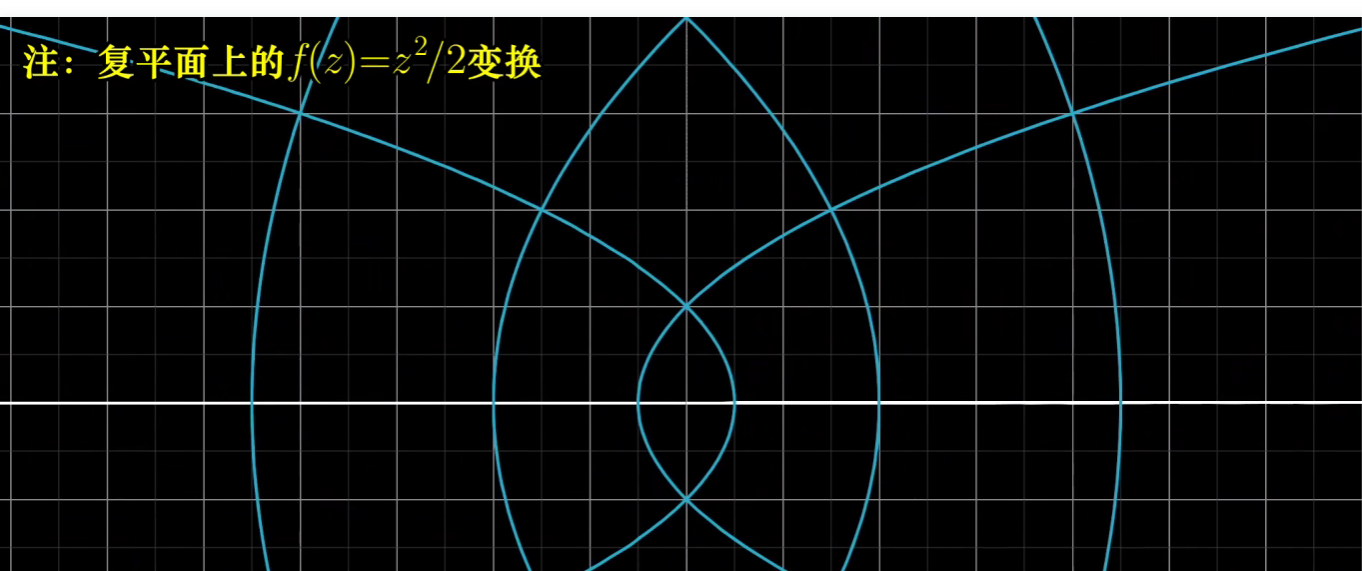
image

原始空间坐标图

image

变化后的空间坐标图
  • 那什么是线性变换呢？

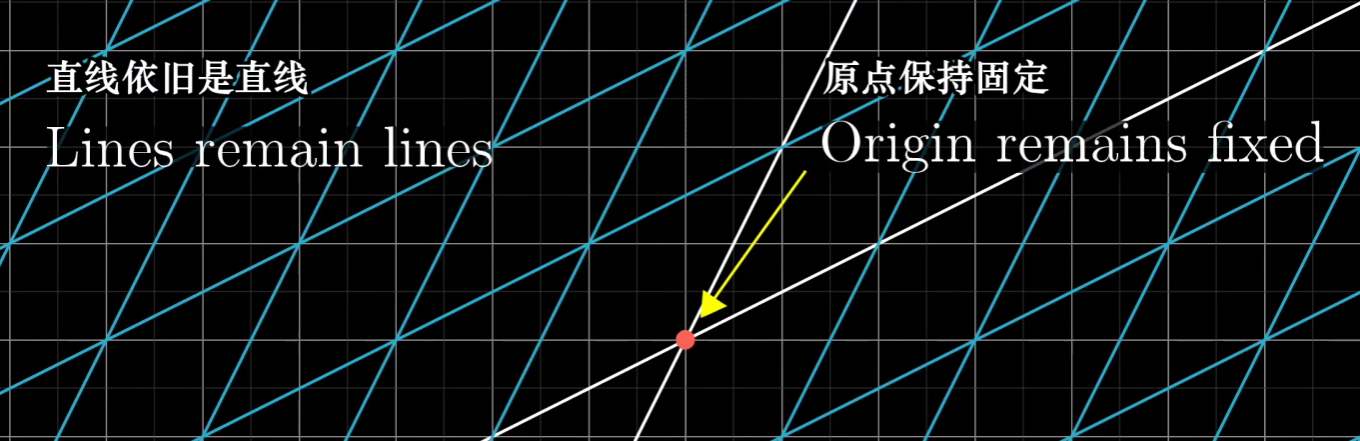
线性变化是要求“保持网格线平行且等距分布，而且原点不变”的变换
image

我们很熟悉地将坐标写成列向量的形式
  • 如何用数值表示线性变换呢？
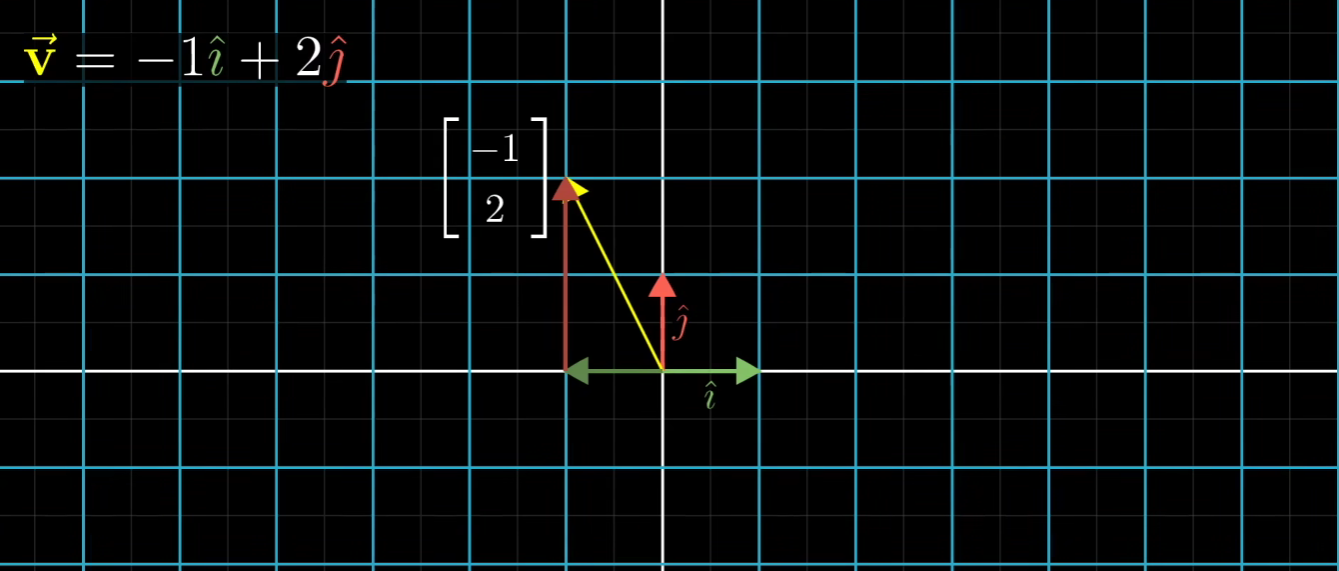
    image
    如上图可以知道，如果上图空间发生变化，那么其原始的基向量也会发生变化
    我们保留原来的网格，画出变化后的网格
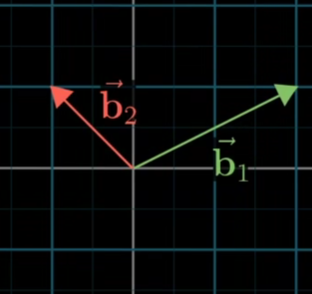
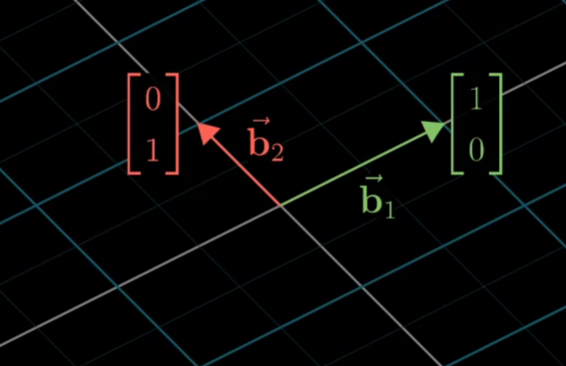
    image
    可以发现原始基向量从i=[1,0],j=[0,1]
    变成了i=[-1,2],j=[3,0]
    然后原始的，相当于伸缩用的标量是不变的

进一步地，一个让人眼熟的东西应该出现了
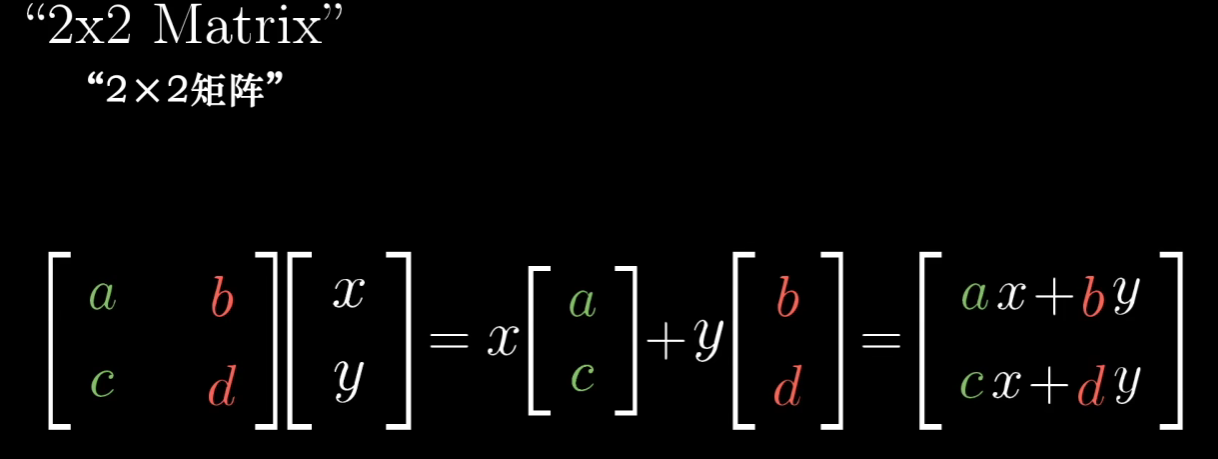
image

所谓的矩阵是原空间中基向量变化后的坐标的列集合，即矩阵代表一个特定的线性变换
所谓[x,y]这样的是原空间中的各个基向量的标量，被称为初始向量，其是不变的
矩阵与向量相乘，就是将线性变换作用于那个向量，可以想象成空间进行了变化

如何理解矩阵相乘和线性复合变换？

通过上面我们可以知道，所谓矩阵是一个空间变换的数值表示，矩阵与向量的相乘是变换作用于向量
那么当空间有多次变换，我们的向量是不是需要乘以多个矩阵？
image

对空间先进行旋转，再进行剪切

初始向量是不变的，我们可以将初始向量抽离出来，进行纯粹的数值计算
image

  • 那么矩阵乘法是如何进行的？又有什么含义？
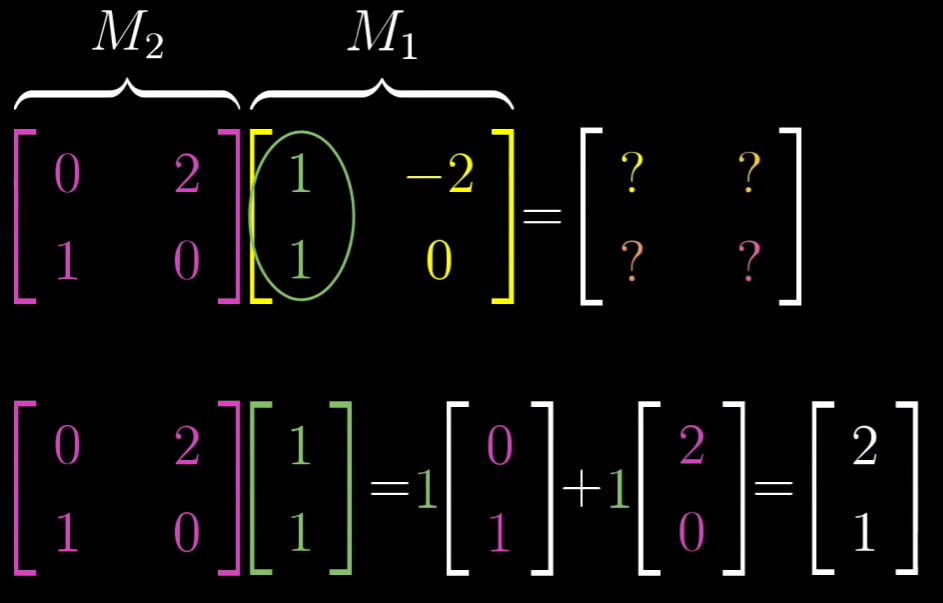
    image

我们知道矩阵的一列其实就是一个基向量变换后的位置，其再经过一次空间变化，然后变成新的位置，上图描述的就是这个过程
更加复杂的矩阵相乘其实表达的含义也就是这样了

如何理解行列式？

在二维坐标下，行列式代表线性变换后，相比于原基向量形成的面积，变化后基向量形成的面积的倍数
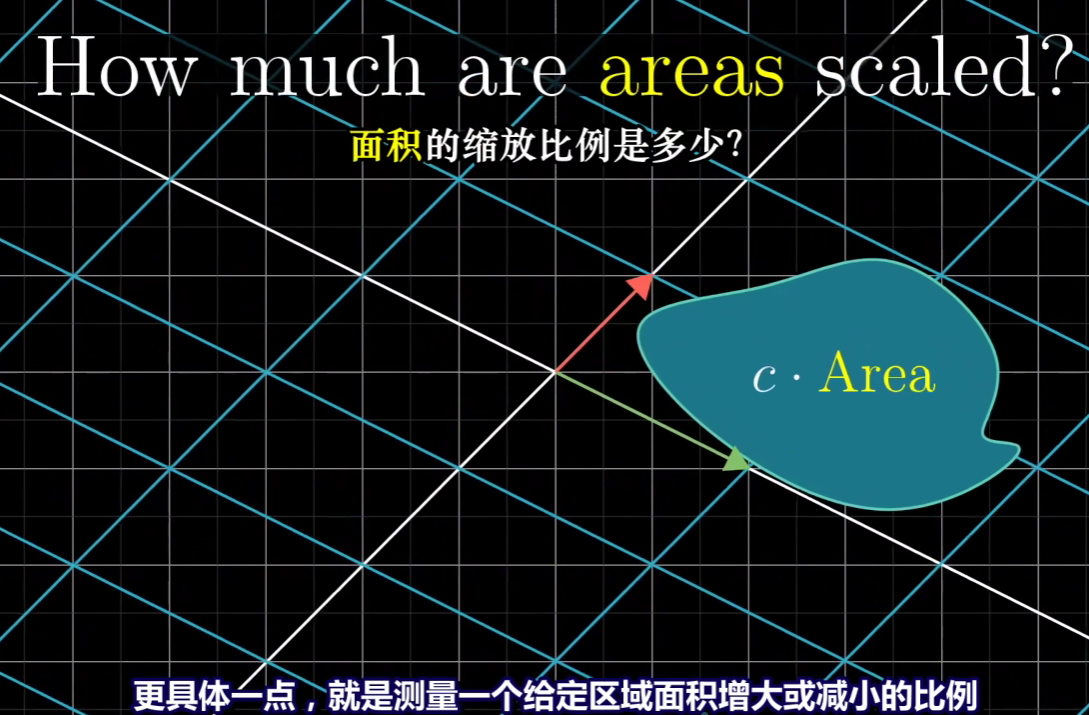
image

such as:

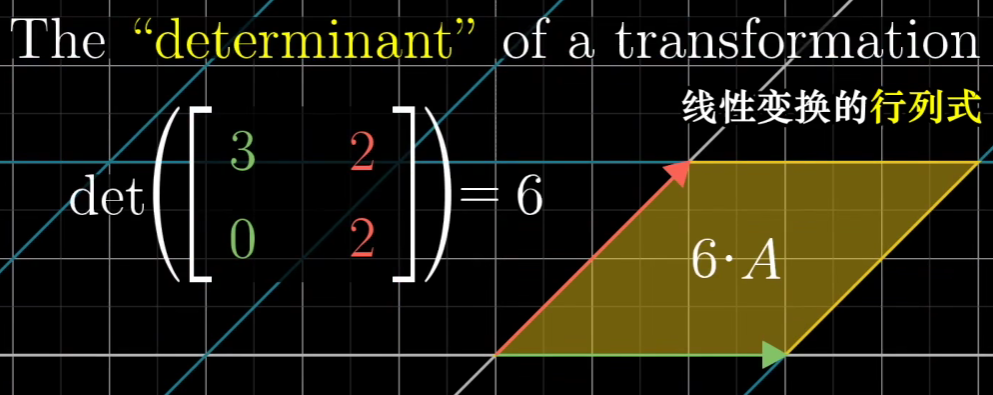
image
image

  • 如何解释行列式是个负数？
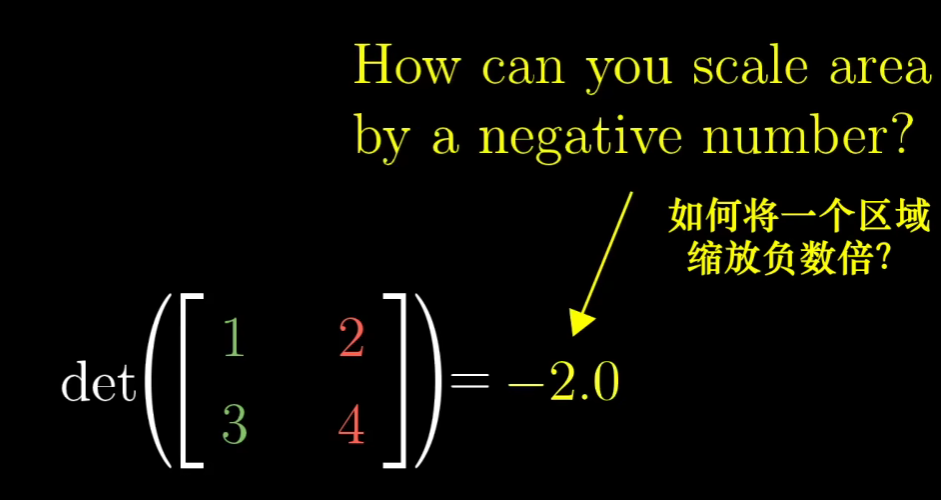
    image

可以想象一下，行列式是正数的时候（二维下），其实相当于将空间进行整体的伸缩
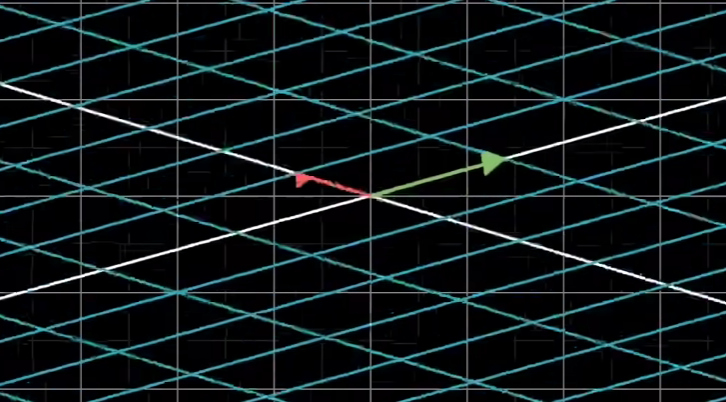
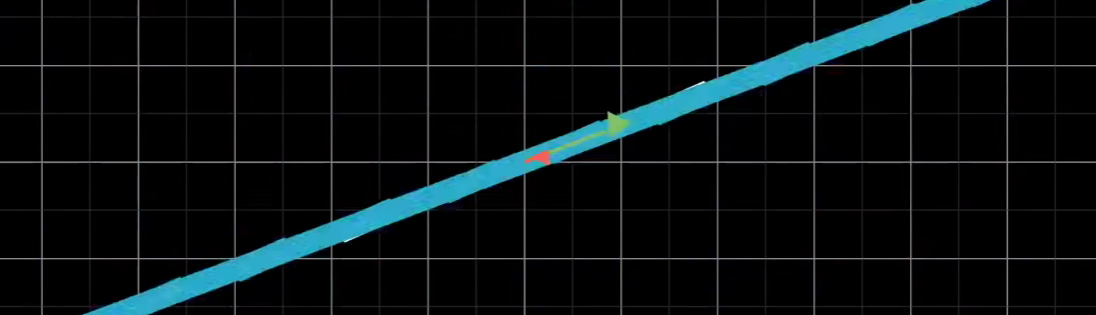
当我们将这个空间拉扯的很紧，变成一条直线的时候
image
行列式就是0了
在负数的时候，其实是进一步像是将空间翻转过来了，在几何含义上就是这个比例加上绝对值了

image

翻转之前

image

翻转之后

三维情况下是如何的？

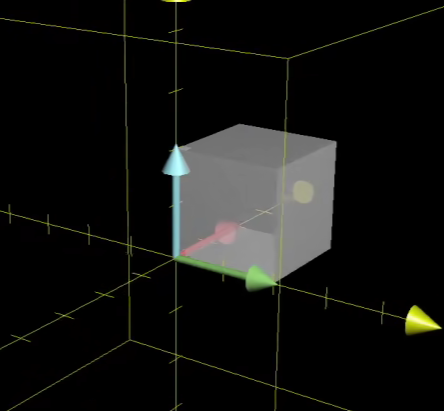
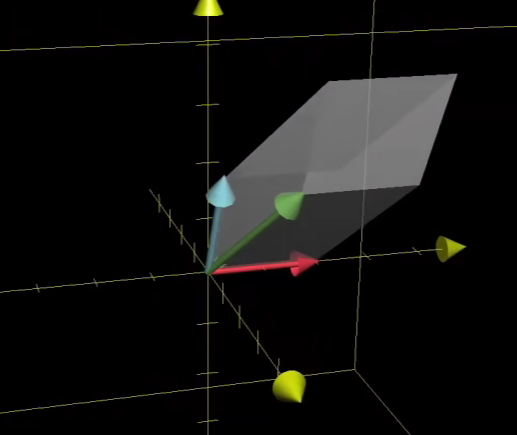
image
image
其实可以推广出行列式是体积的比例伸缩

线性方程组如何理解？

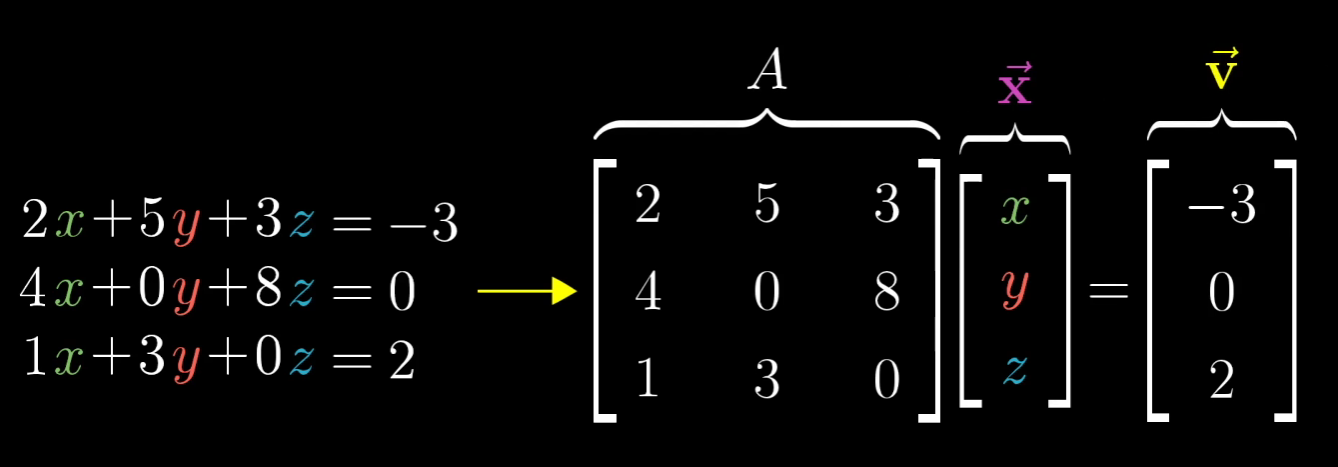
image
X是未知解
更加我们上面的知识我们可以这么理解

所谓的线性方程组是找到原向量X，使得经过线性变换A后得到V
我们知道A是基向量经过空间变化后新的基向量的集合，乘以A相当于对空间进行了一次变化
乘以X相当于对对应的基向量进行伸缩变化
AX这个整个过程可以想象成，从原来的:
image
经过空间线性变换，到现在的：
image

如果我们能够知道空间的逆变换过程，那么我们是不是可以从已有的V变到未知的X
因为矩阵就是用数值表述空间线性变换的东西
那么我们是不是只要知道逆矩阵就可知道逆变换了？
image

解

一般情况下A是有逆矩阵的，这个时候，X是有唯一值的

可以想象一下在A与V都是确定的情况下，变换的情况是唯一的，X也是唯一的


* 那么什么时候A是没有逆矩阵的呢？

image
想象一下当det(A)=0的时候，是不是说明我们的基向量形成的形体没有大小了，即形成平面/线/点....了，即发生降维了

想象一下，在三维中的一个有体积的形体可以通过空间变换使得这个有体积的形体变成平面，变得无体积了

或者想象一下再二维中，一个有面积的形体通过空间变换使得这个有面积的形体变成线，变得无面积了

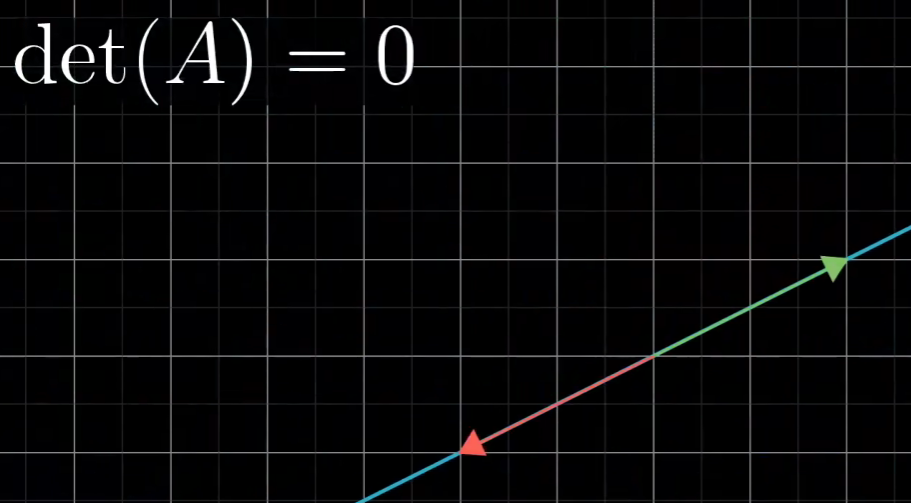
image

↓

image

  • 为何说当det(A)=0时，A没有逆矩阵？

想象一下，假如就是在二维上，是否存在一个空间变换使得一条线变成一个平面？
有，但是这并不是函数能够做到的，因为这个要求 输入（一条直线）要映射到多条直线上（全部直线合在一起就是平面），即一对多，这个并不是函数能够做到的
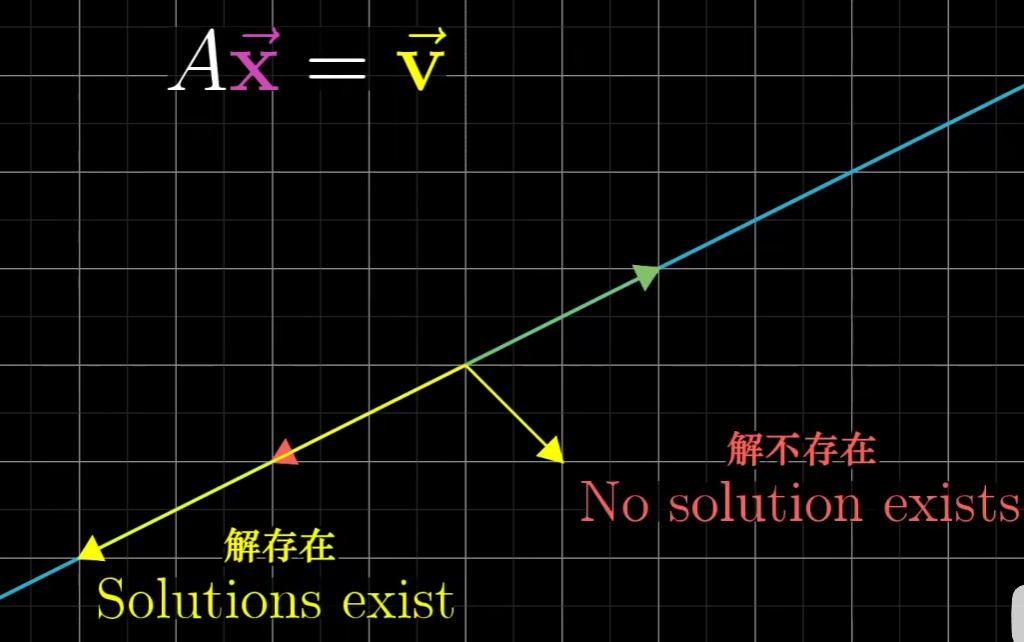
image

  • 解不存在
    image

当det(A)=0时，解是可能存在的
这个就要求v正好在经过AX后形成的平面/线/点...的上面，

秩

image
比如在原先的三维空间中的体积形体，经过空间变换后形成了平面形体

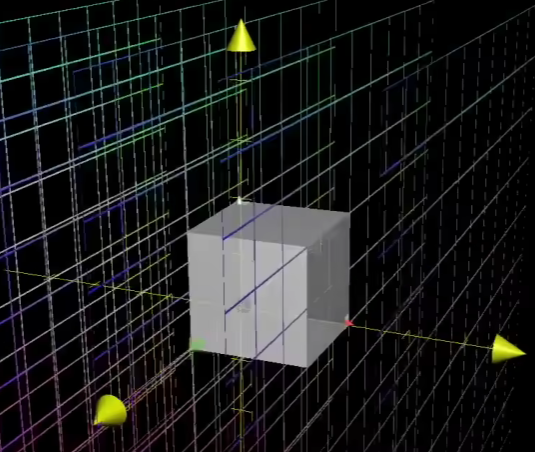
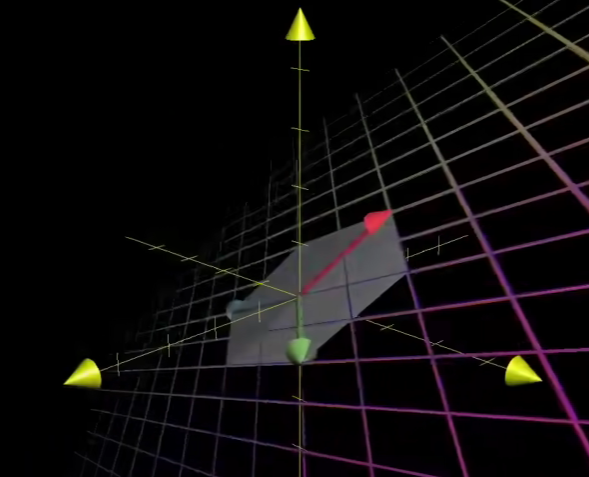
image

↓

image
那么这个时候秩就为2

矩阵的列代表基向量在空间中的位置，有多少列就代表有多少基向量，就代表这个空间中真正的维度是多少
image
当输入矩阵X经过A线性变换后得到的维度与初始维度相同，我们称这个时候的秩为满秩
经过一些推导：满秩->形体没有被降维->A可逆
所以不是满秩那么就A不可逆

矩阵的行个数代表当前观测的空间的维度

零空间/核

image

  • 对于线性变换后是满秩来说
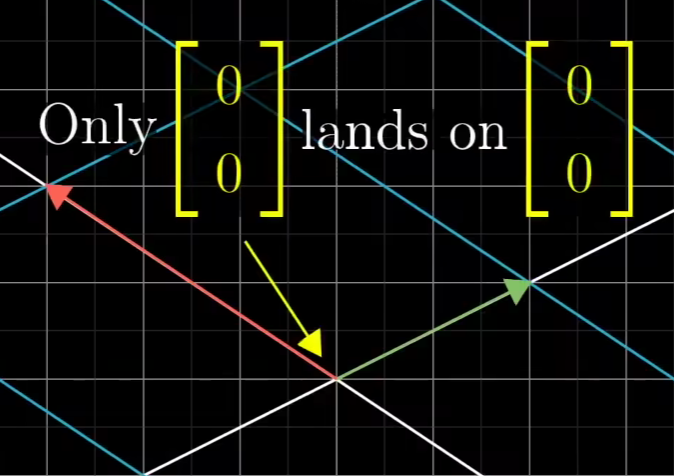
    image
    有且仅有零向量，在经过变化之后还是落在原来的零向量位置处

  • 对于非满秩来说
    因为非满秩会将某一维度压缩，所以会有一系列向量都变成了零向量
    如下是三维空间中：
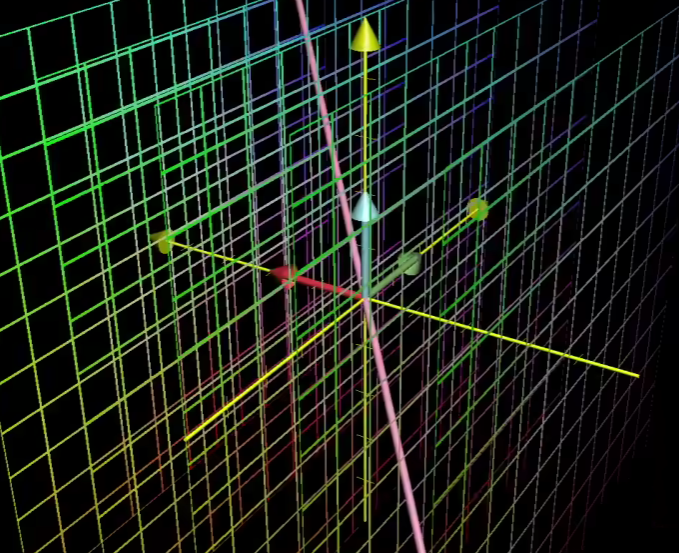
    image
    经过线性变化后空间成为了平面：
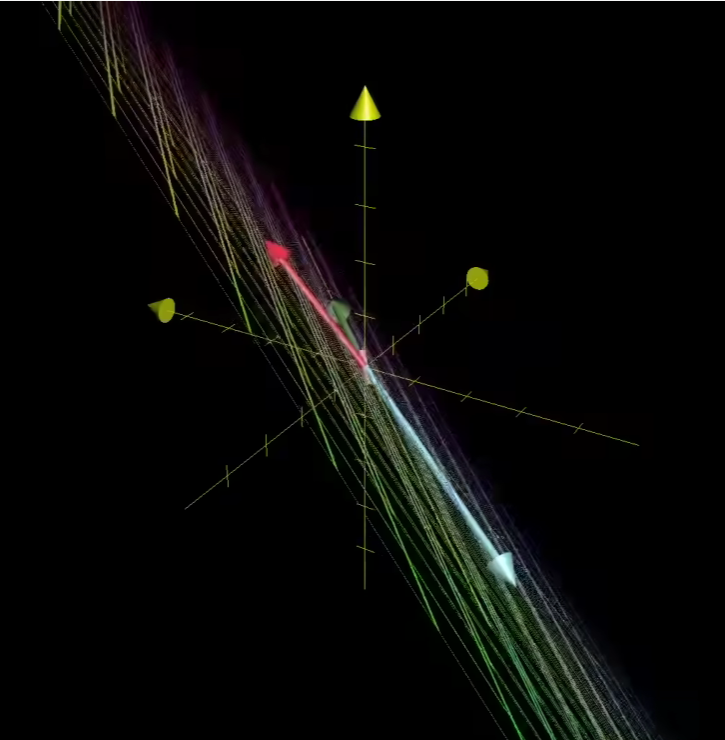
    image
    这个时候就有原来三维空间中一条线变成了零向量（可以理解为一条线被压缩成了一个点）

点积

所谓点积就是形如：V·W，W在以V为轴上投影的长度*V的长度
当W与V同方向，长度>0；W与V垂直，长度=0；W与V反方向，长度<0


对于要理解这一点我们可以从线性变换的角度来思考
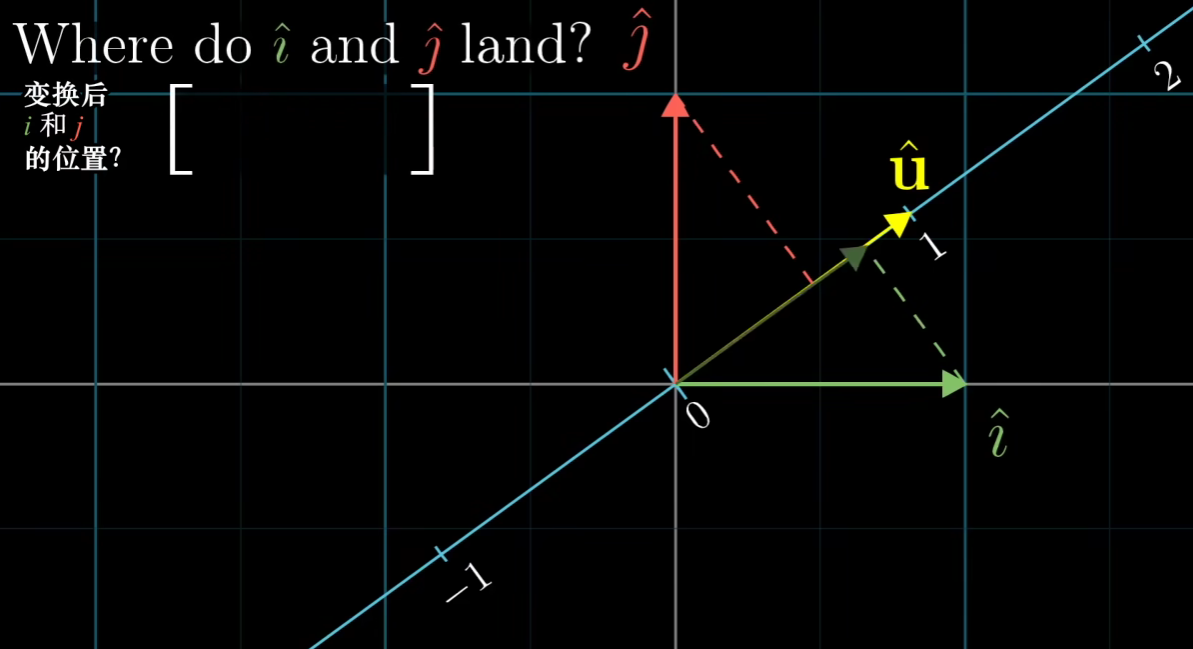
image
现在我们以u为轴，进行空间线性变换的时候基向量变换到u所在的线上（即发生了降维）。变化后的基向量，也就是矩阵为[ux,uy] (更加对称性获得)、


然后对于原来的初始向量，映射到新的空间中就为：
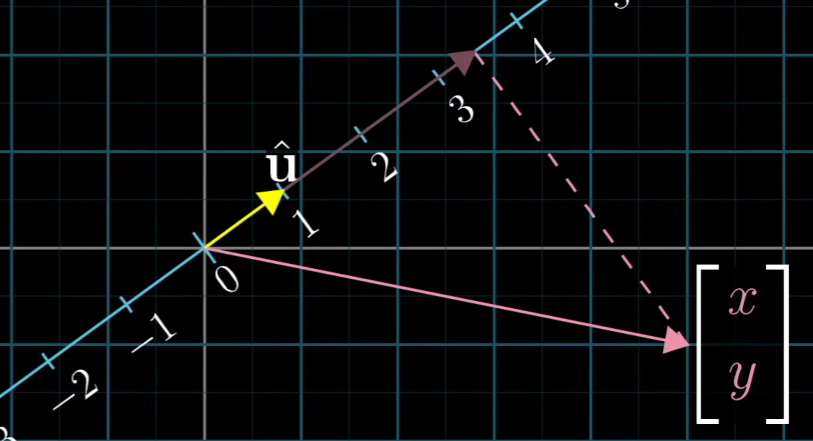
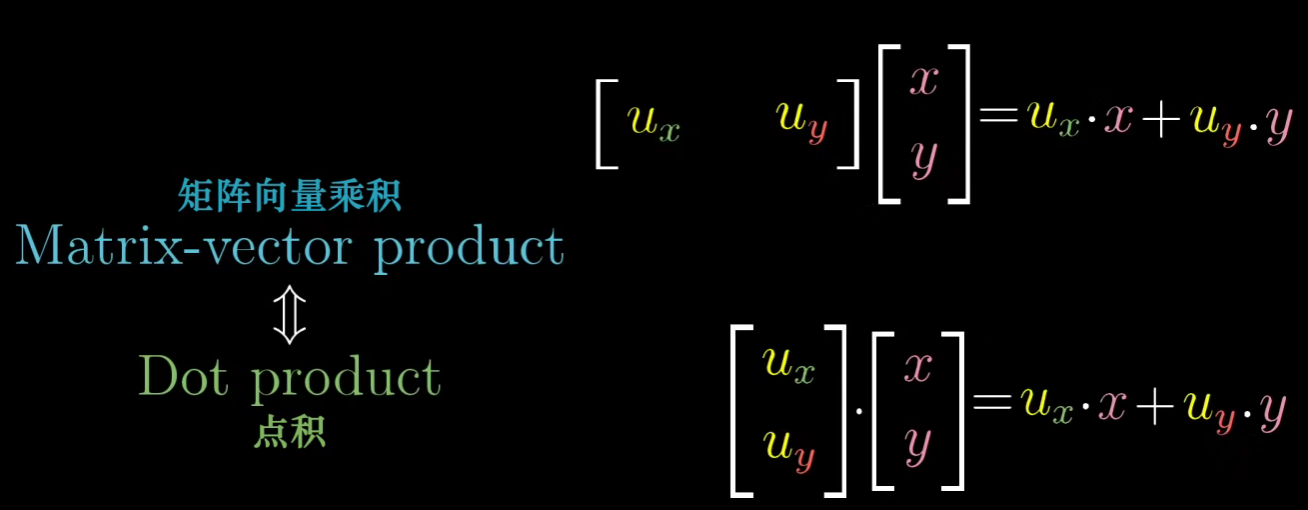
image

image
因为u是单位向量，所以其长度为1，所以U·W为W在以U为轴上投影的长度U的长度=1W的长度

叉乘（叉积）

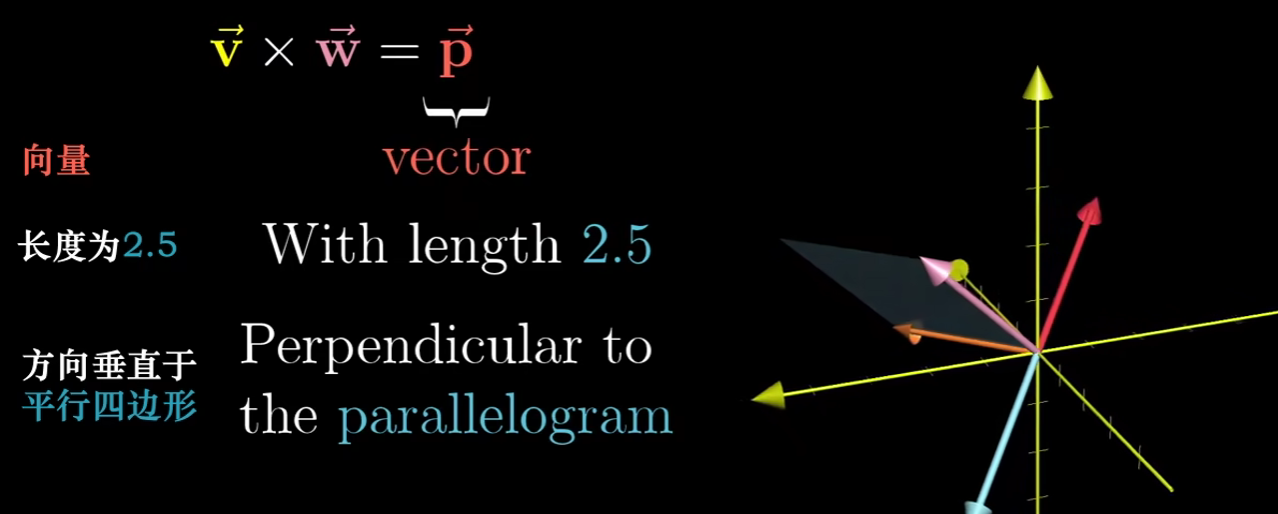
image
image
image
image

基变换

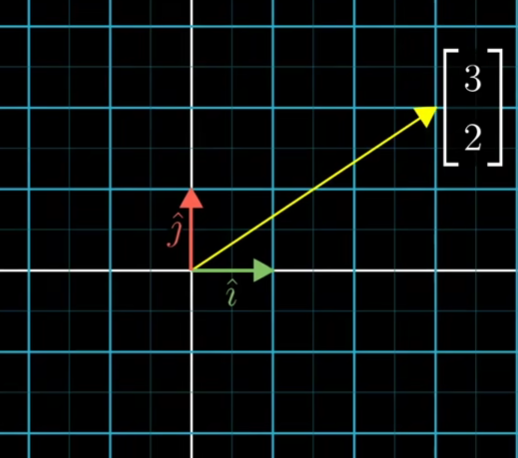
image
当我们以一种常见的基向量去描述一个向量[3,2]时，很好描述，我们只要看着坐标网格线数一下就行了，就是[3,2]
因为其实向量是对基向量的伸缩变换


但是当用其他基向量来描述一个向量时，又是如何？
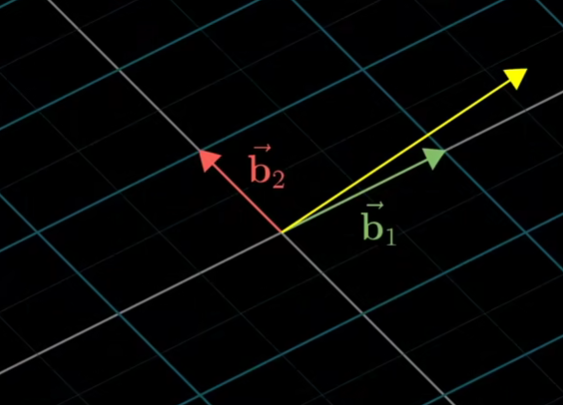
image
这是用另一组基向量描述向量[3,2]，在这组基向量下，会用如下来描述：
image

  • 可以看出不同的基向量下对相同的一个向量描述是不同的，那么有没有什么办法可以让不同基向量下对向量的描述可以相互转换？即如果我知道在基向量A下一个向量描述为[3,2],我想知道在基向量B下向量[3,2]应如何描述
    下面我用“我们的视角”表示一般基向量下的情况，用“她的视角”表示其他基向量下的情况

image
如上是在我们的视角下，看到的她的视角下的基向量
但是对于她来说，她的基向量就是[[1,0],[0,1]]
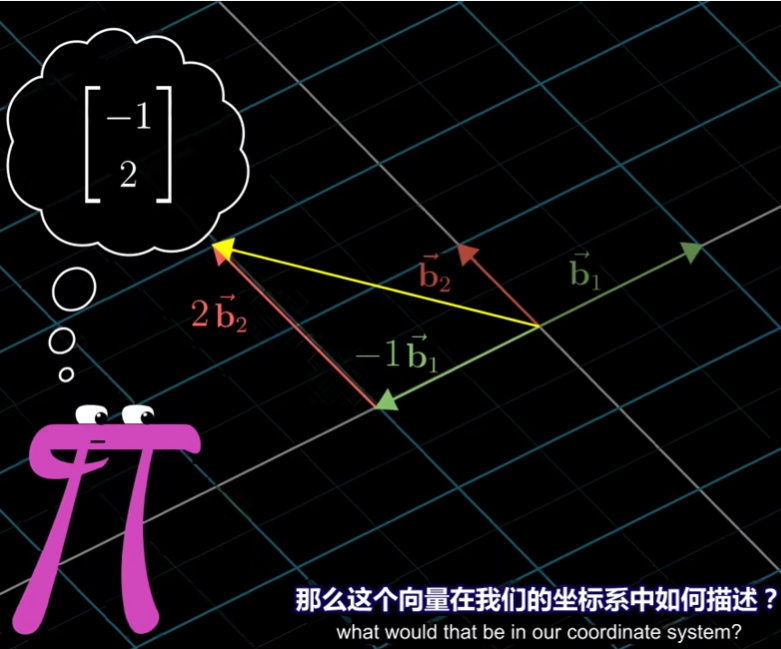
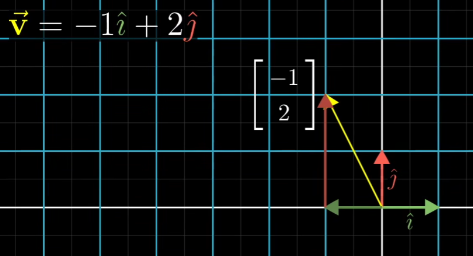
image


image
如上，她在她的基向量下表示了[-1,2]这样一个向量
对于这个向量，在我们的视角下如何表示？
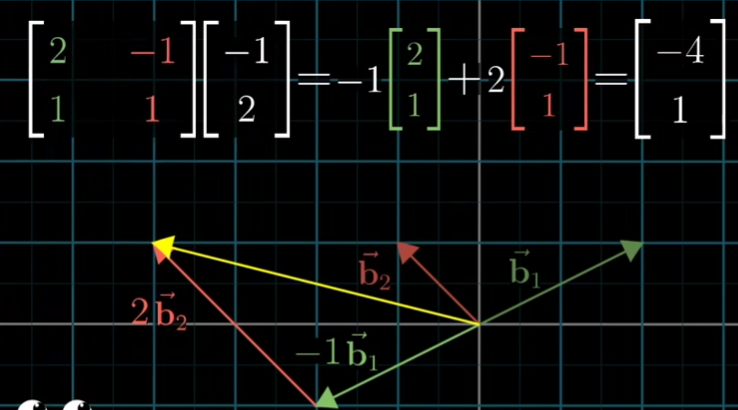
image

解决方法是：我们用在我们视角下表示她的基向量，然后与她描述的向量进行矩阵乘法，得到的就是我们的角度下描述这个向量
AX=V
A表示成在我们的视角下她的基向量，X是她描述的向量，V是我们视角下描述的向量
如果反过来，我们视角描述了一个向量V，在她的视角下如何描述？
答案已经明显了：即X=A^-1V


  • 上面我们解决了不同基向量下对于同一个向量如何转换描述的方法，接下来我们来讨论一下：在不同基向量下，如果空间发生了线性变换，即已知A基向量下空间发生了逆旋转90度后得到的新基向量，那么在B基向量下空间也发生了逆旋转90度，她的新基向量是什么？

因为我们视角下发生空间线性变换后是好进行知道的，我们可以先用我们视角下描述她视角下的基向量A，然后发生空间线性变换M，变换后在我们的视角下她视角下的基向量为MA，然后再通过A^-1 WA 变成她视角下的新的基向量
image
A^-1MA就是在她视角下进行空间线性变换
image
image
image

特征向量与特征值

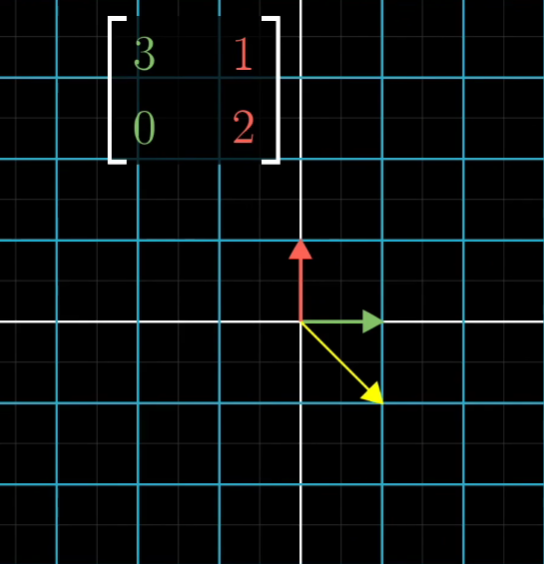
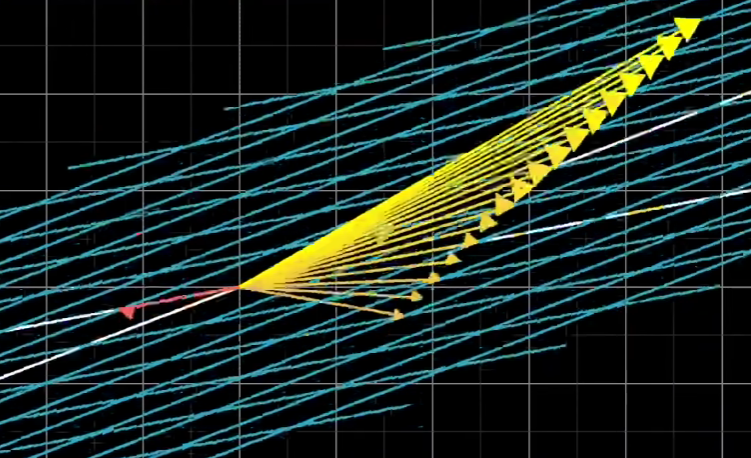
image
在进行空间线性变换时，绝大多数向量都离开了他们原先的位置，但是确实存在一些向量没有
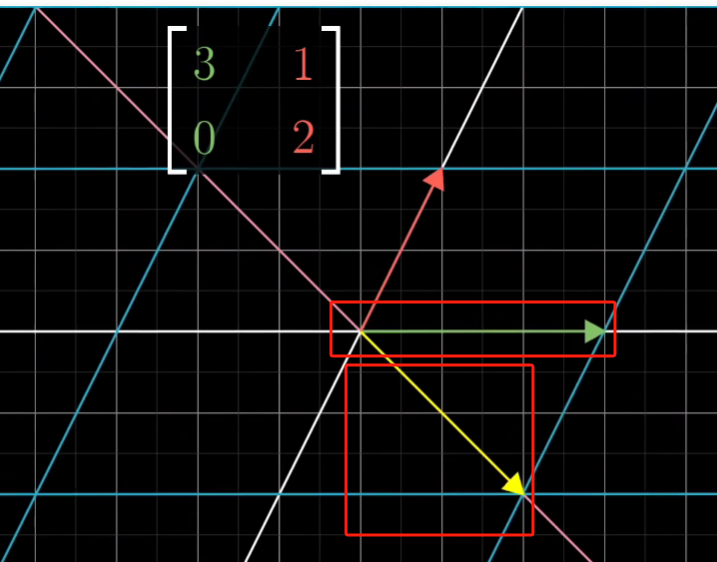
image
对于这些向量，他们在进行空间线性变换的时候只是受到了伸缩而已，并没有离开他们的位置，这些向量我们称之为特征向量。
而对于伸缩的尺度，我们称之为特征值
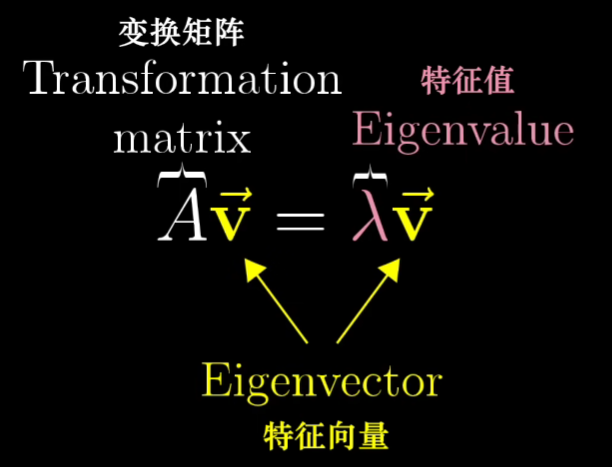
image
所以我们在学线性代数的时候经常能看见上述公式，其表达的含义就是向量V在经过线性变换A后，只是受到了伸缩入而已


我们常常也能将公式转换为如下：
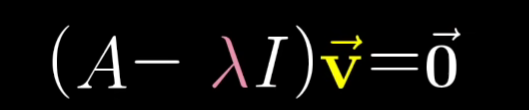
image
其中的A-入I就是一个新的矩阵，它代表了一个空间线性变换
还记得我们上面的内容吗？在V不是零向量的情况下，一个空间线性变换将向量变成了零向量，那么就是降维了（对空间进行了压缩）
即det(A-入I)=0
然后通过最终得到的det(A-入I)=0，我们就能在知道A的情况下很愉快地求解入了！

特征基

如果基向量是特征向量会发生什么？
image
会发生矩阵是一个对角矩阵
解读它的方式是：每一个基向量都只是在最初始的单位向量上进行了伸缩变换，即对角线上的值就是他们的特征值入

环境配置

安装环境

血的教训：不要到网上随便找教程，最好按照官网的来按照
官方文档
视频教程


然鹅我已经走了错误的道路，已经回不去了
网上安装教程

以后我启动Jupyter记事本需要：

  1. image在这里输入cmd
  2. conda activate gluon
  3. jupyter notebook
  4. 然后就是我的笔记本没有显卡，跑不出图来，那就用百度飞桨吧

一些库

在数组算术计算方面， NumPy 提供了大量的数学函数。NumPy 的底层主要用 C语言编写，因此它能够高速地执行数值计算。NumPy 还提供了多种数据结构，这些数据结构能够非常契合的应用在数组和矩阵的运算上。

  • Matplotlib
    image

Matplotlib 是一款用于数据可视化的 Python 软件包，支持跨平台运行，它能够根据 NumPy ndarray 数组来绘制 2D 图像

类型转换

首先利用pandas进行读取数据，将数据转化为numpy的矩阵，再利用pytorch的tensor，将其转换为张量进行计算

pandas 基本用法

pandas 中读出来一般是将数据转换为DataFrame的数据结构
其默认是列操作：
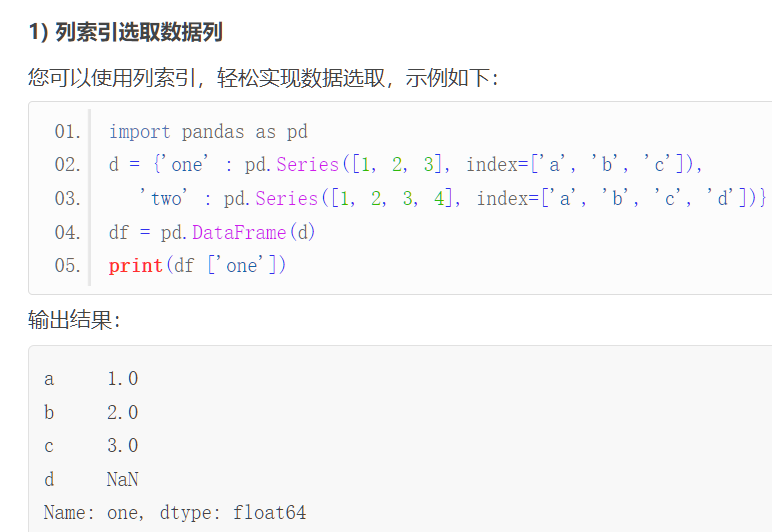
image
image

也可以按照行操作：
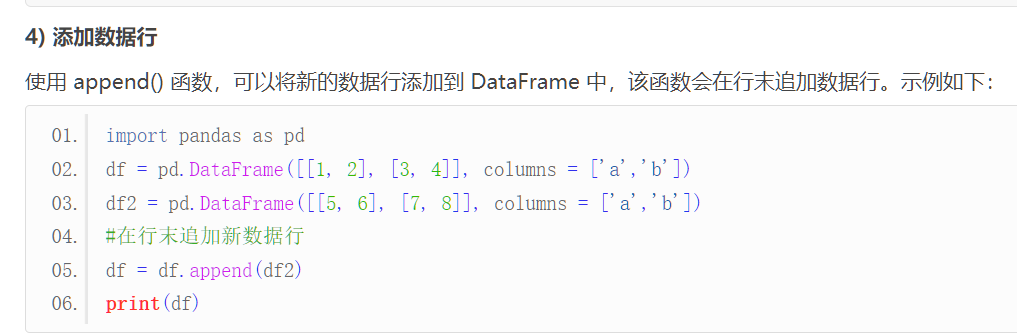
image
image
image
按照行操作时基本上根据行的index进行操作

张量机制

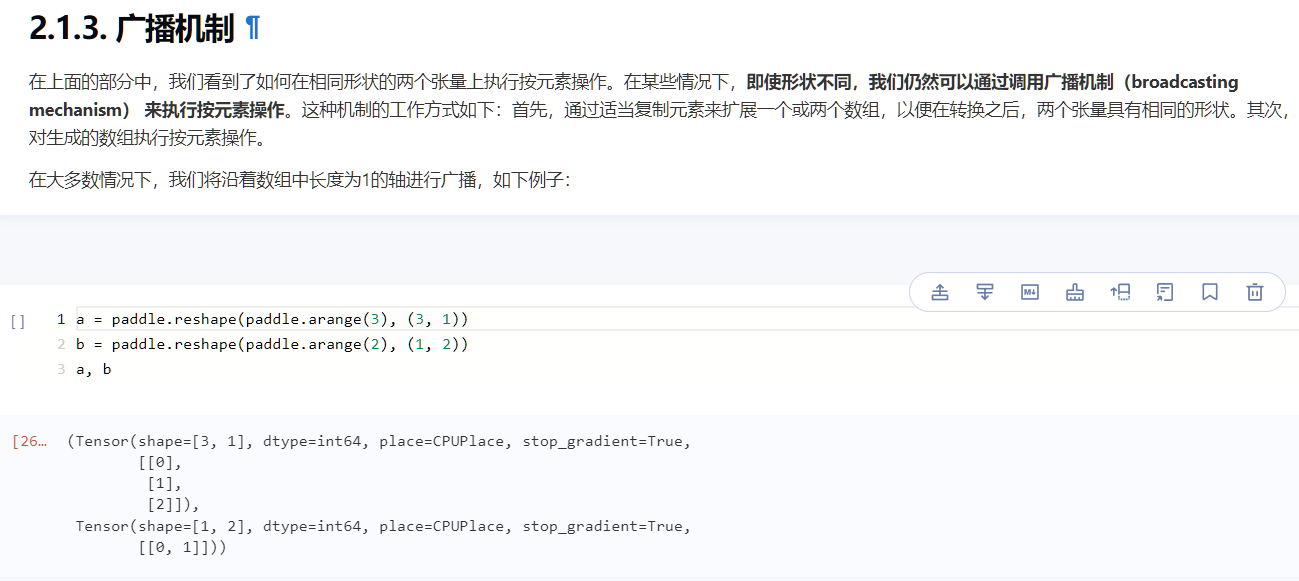
image
可以看到，a,b两个张量形状不一样，但是却能够直接相加 a+b
这里的直接相加是pytorch进行了操作，他将a与b变得形状相同了
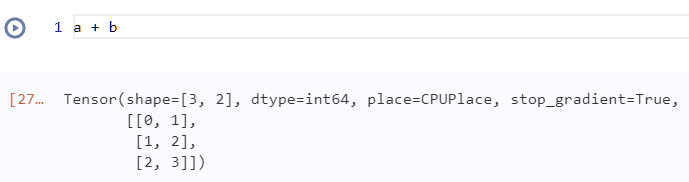
image
这里的操作是将a行列复制，变成了2列，即为3x2的矩阵
将b进行行复制，变成了3行，即为3x2的矩阵

索引和切片

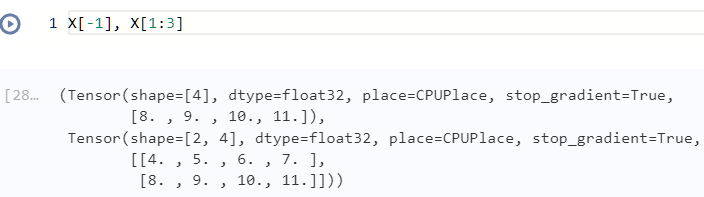
X：image
image
当[]中只有一个数时，则是按照0轴取，0轴是列，即可以将X看作：
X=[a1,a2,a3]
a1=[0,1,2,3],a2=[4,5,6,7],a3=[8,9,10,11]
那么每取一个就是取出一个ai出来

pytorch中对轴的理解

如果有A为一个张量：torch.size([n1,n2,n3....]),那么在0轴的长度为n1,1轴的长度为n2，...以此类推

比如A_sum_axis0=A.sum(axis=0) 当A原来是torch.Size([5,4]),那么就相当于将对应轴的那个长度去掉
即操作完后A形状变成了torch.Size([4])


比如A_sum_axis0=A.sum(axis=0,keepdims=True),当A原来是torch.Size([5,4]),那么就相当于将对应轴的那个长度变成1
即操作完后A形状变成了torch.Size([1,4])

矩阵计算

矩阵求导

image
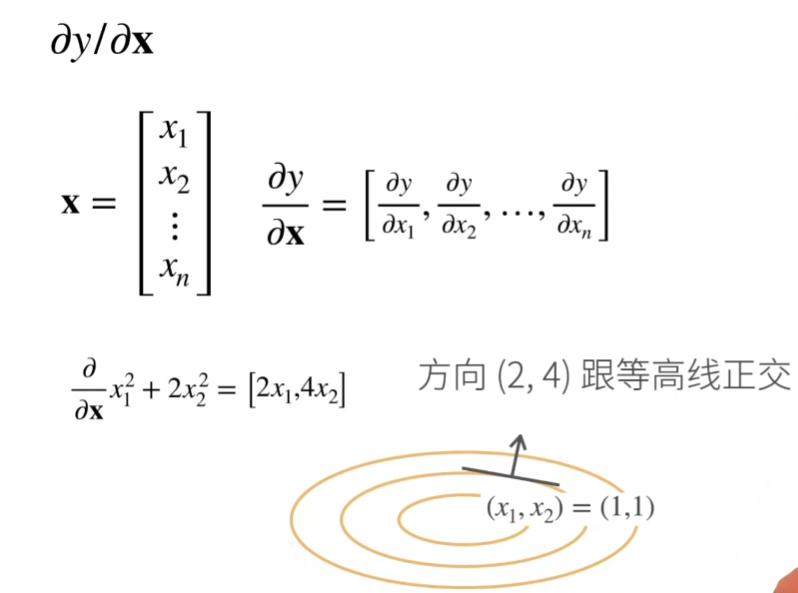
我们通过上图来理解一下矩阵求导；
当x为向量，y为标量，即有y=a1x1+a2x2+...这样的形式，对x求导后，即是一个行向量。
这样的一个行向量即为梯度。

如何理解梯度？梯度指向的是值变化最大的方向。
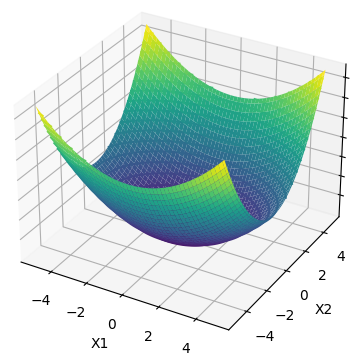
如图上的圆环是方程z=x12+2*x22的等高线，下图是方程的3d图
image

更多详细内容

sum求和

image

积

Hadamard积

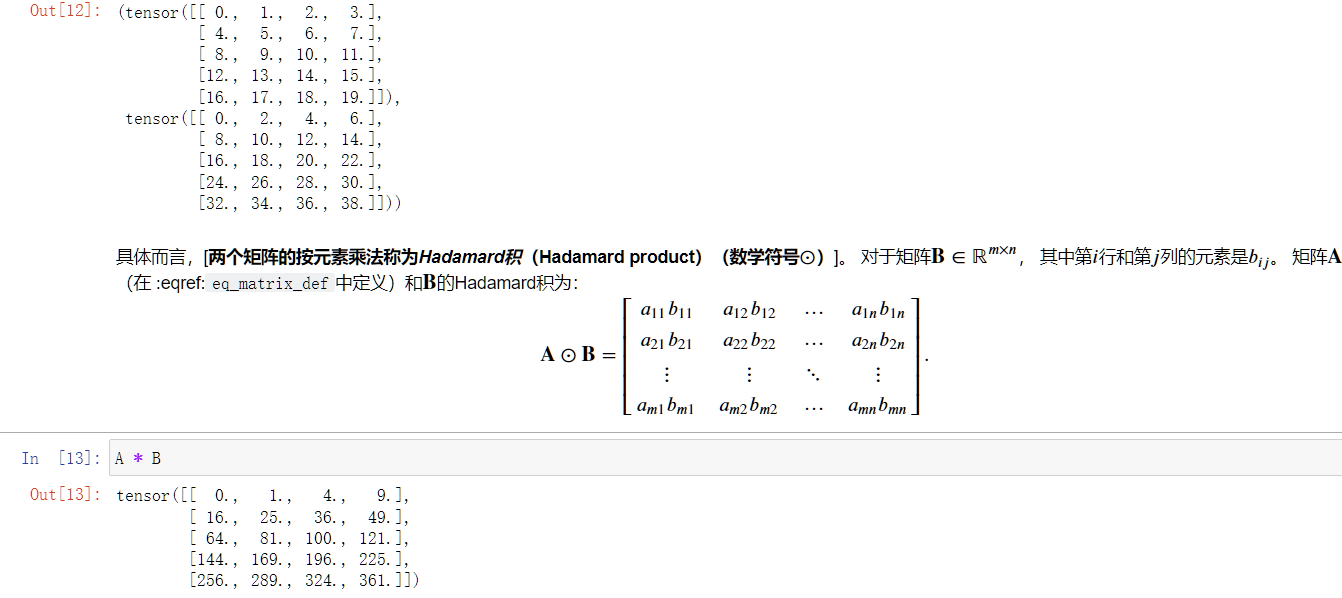
image
注意这里Hadamard积可以直接使用A*B

点积

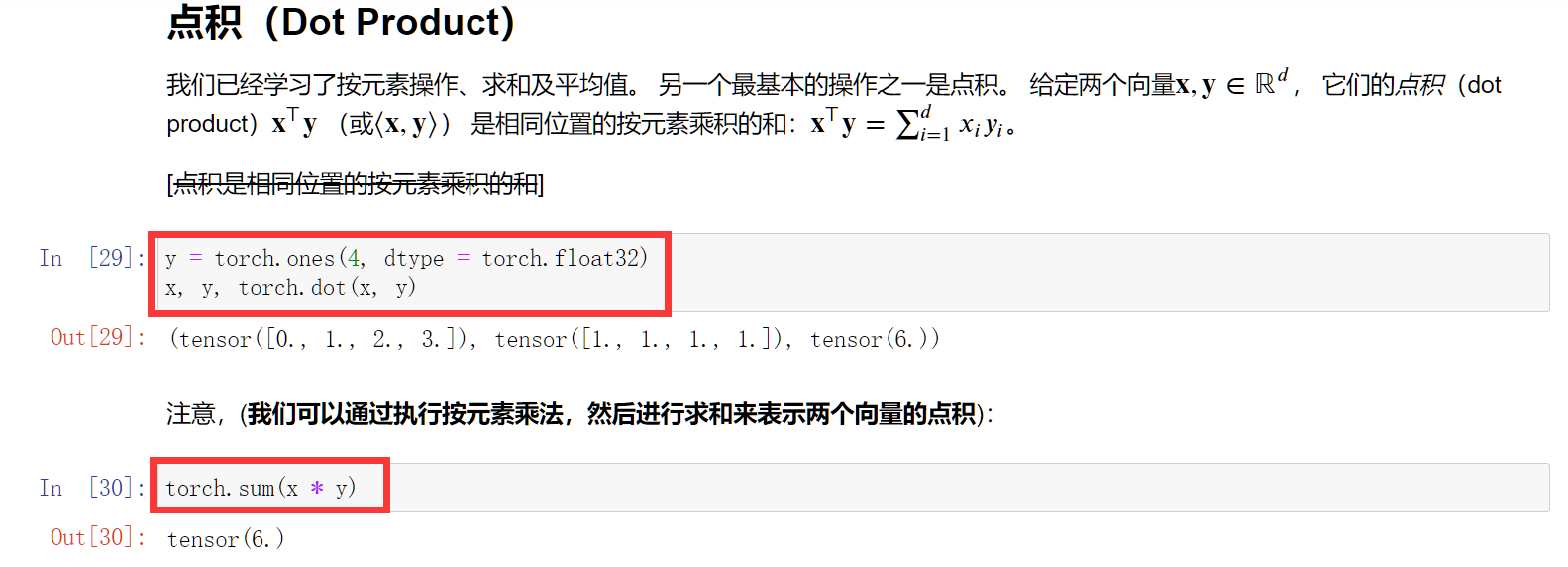
image

矩阵向量积

torch.mv(A, x)

矩阵乘法

torch.mm(A, B)

范数

torch.norm(torch.ones((4, 9)))

画图

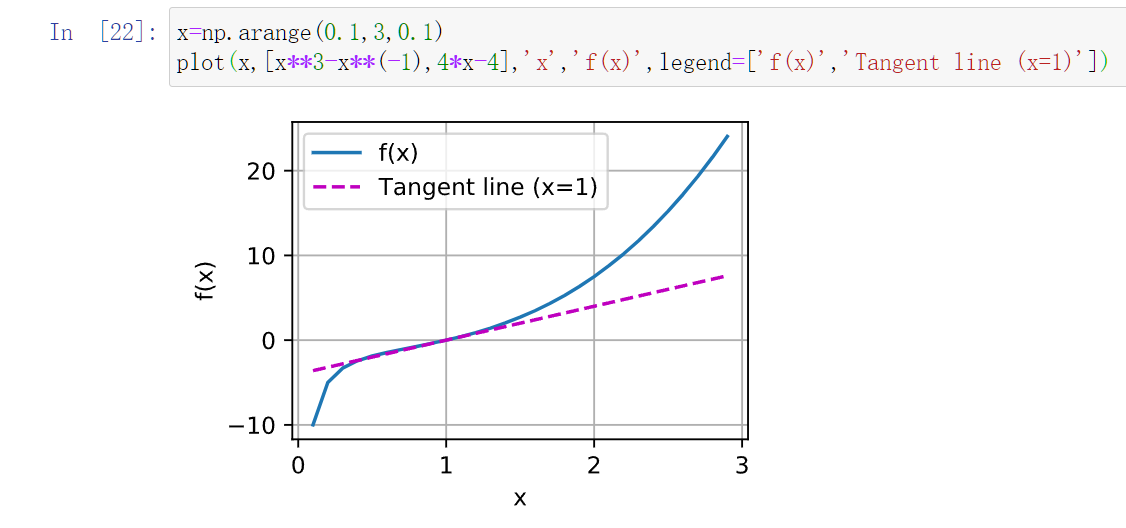
image
利用np.arange生成出范围数

%matplotlib inline
import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2l
def use_svg_display():  #@save
    """使用svg格式在Jupyter中显示绘图"""
    backend_inline.set_matplotlib_formats('svg')
    
def set_figsize(figsize=(3.5, 2.5)):  #@save
    """设置matplotlib的图表大小"""
    use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize

#@save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    """设置matplotlib的轴"""
    axes.set_xlabel(xlabel)
    axes.set_ylabel(ylabel)
    axes.set_xscale(xscale)
    axes.set_yscale(yscale)
    axes.set_xlim(xlim)
    axes.set_ylim(ylim)
    if legend:
        axes.legend(legend)
    axes.grid()

#@save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,
         ylim=None, xscale='linear', yscale='linear',
         fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    """绘制数据点"""
    if legend is None:
        legend = []

    set_figsize(figsize)
    axes = axes if axes else d2l.plt.gca()

    # 如果X有一个轴，输出True
    def has_one_axis(X):
        return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
                and not hasattr(X[0], "__len__"))

    if has_one_axis(X):
        X = [X]
    if Y is None:
        X, Y = [[]] * len(X), X
    elif has_one_axis(Y):
        Y = [Y]
    if len(X) != len(Y):
        X = X * len(Y)
    axes.cla()
    for x, y, fmt in zip(X, Y, fmts):
        if len(x):
            axes.plot(x, y, fmt)
        else:
            axes.plot(y, fmt)
    set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
    
    
Y1=[]
Y2=[]
X=torch.arange(-10,10,0.1)
for x in X:
    x.requires_grad_(True)
    y=torch.sin(x)
    Y1.append(y)
    y.backward()
    t=x.grad
    Y2.append(t)
Y1=torch.tensor(Y1)
Y2=torch.tensor(Y2)
plot(X,[Y1,Y2],'x','sin(x)')

'''绘图样例
x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])
'''

自动微分

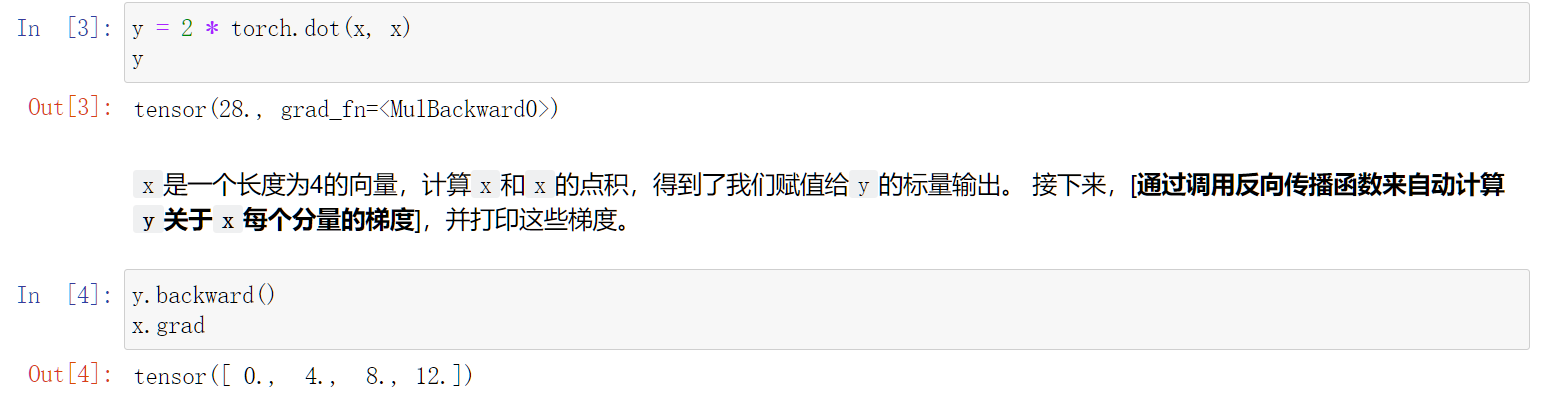
image
image
y.backward()会计算梯度
x.grad查看梯度
x.grad.zero_()因为累积梯度的原因，当需要清空梯度时，利用这个函数
自动微分只能针对于标量 （为啥？）

配置时遇到的bug

  • ValueError: check_hostname requires server_hostname
    原来是我没有关VPN梯子。。。。
posted @ 2023-09-16 16:56  次林梦叶  阅读(46)  评论(0)    收藏  举报