数学建模----预测（评价关系的模型） 线性回归（回归分析）

回归分析的目的：

 

 

 

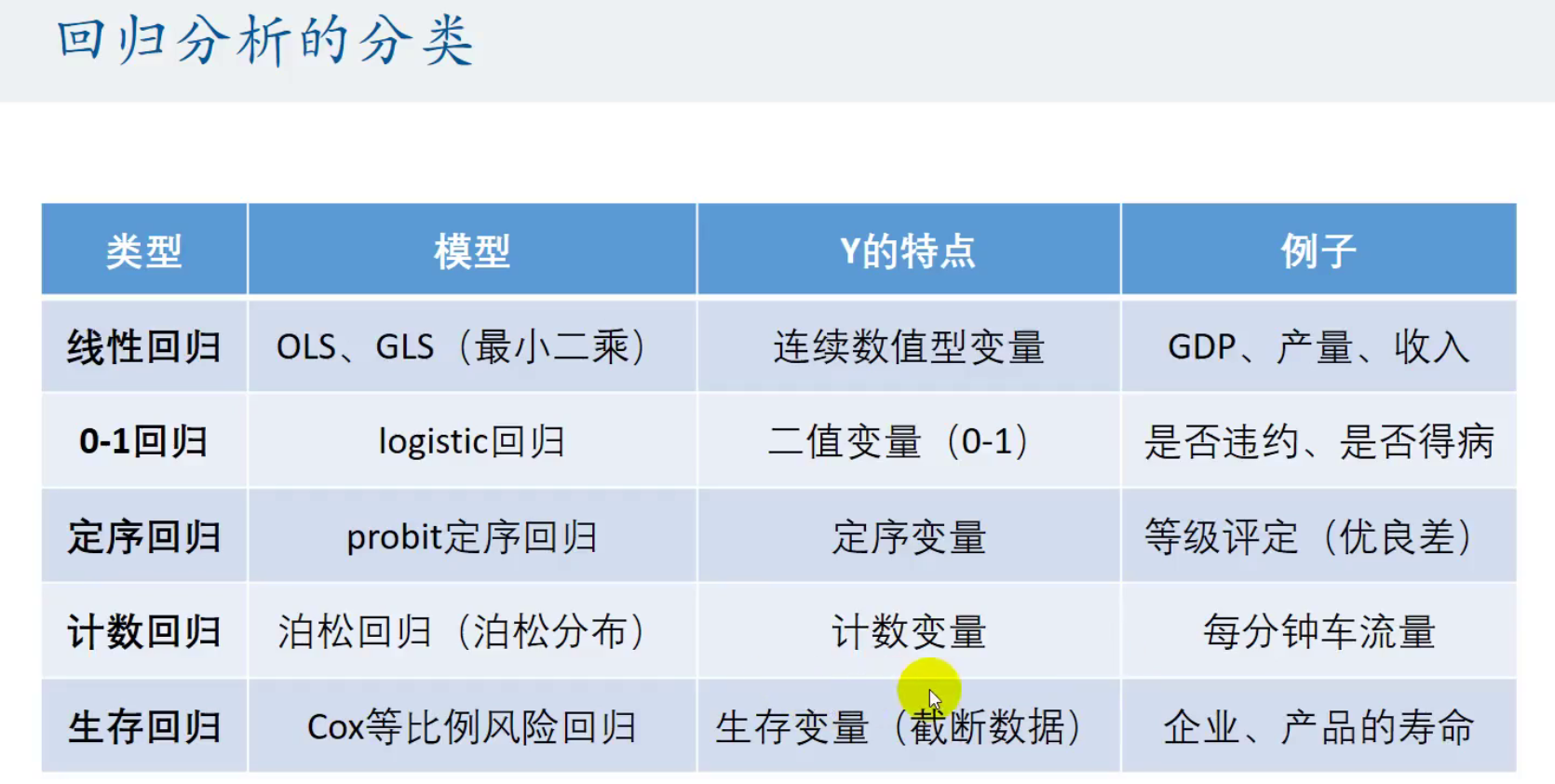
回归分析 数据的分类以及数据从哪里来？

 

 

 

 

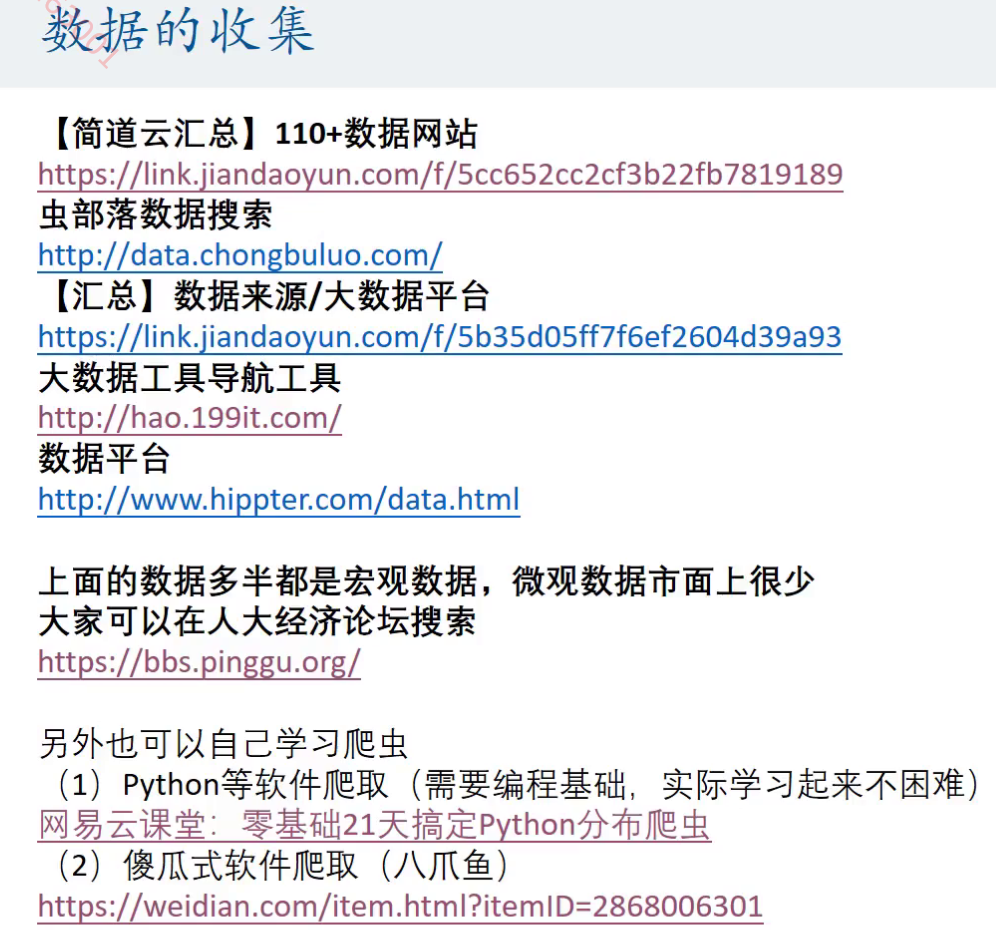
线性回归原理部分：

　　如果想要做回归，那么最好样本数量>=自变量个数+1

　　

 　　

 　　所谓一元线性回归就是只要一个自变量，多元线性回归有多个自变量

　   这里一元线性回归与拟合有点相似 是因为回归的目的之一就是通过x来预测y

 

　　总之：在一元线性回归中，为了使更接近y，我们需要让残差尽量小

 

　　对于线性的理解：

 　　　　

 　　　　比如第一个函数，我们可以将Inx 变成 z，这个时候这个函数看起来还是线性的

　　　对于数据进行预处理是因为，如：

　　　　既然我们将Inx当成了一个整体来看，那么原先是x的数据要变成lnx 的数据

 

　　对于内生性的讨论：

 　　　　

　　　　　不满足一致性的含义是：

　　　　　　即使样本容量再大，最后的结果也是与真实的结果不同

　　　　　　即不能收敛

 

　　　　

 　　

 

　　　　内生性的蒙特卡罗模拟：

　　　　　　即我们随机出来数据，来看看内生性对回归系数的影响

 　　　　　　　　

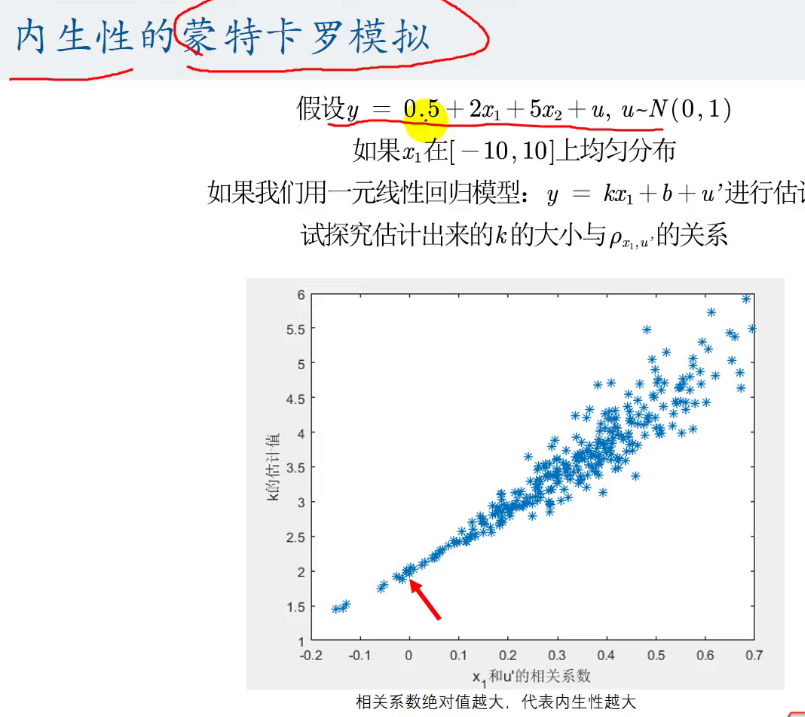
　　　　　　　　这里正确的函数是：y=0.5+2x1+5x2+u

　　　　　　但是我们这里故意让没有添加上自变量x2

　　　　　　 那么这个时候其实这个u'是包含了我们的u和x2的

　　　　　　观察u'与x1的相关系数 其与回归系数k的关系是什么？

　　

%设置图的点数，即进行多少次实验
ts=300;
K=zeros(ts,1);
R=zeros(ts,1);
for i=1:ts
    %每一次实验的样本点数
    n=30;
    %随机出x1,-10<=x1<=10
    x1=-10+rand(n,1)*20;
    %随机出x2
    tu=normrnd(0,5,n,1)-rand(n,1);
    %因为我们模拟出来的是内生性，所以x2与x1有点相关性
    %但是我们并不清楚x2与x1的相关性到底是什么所以要加上一个随机数tu
    x2=0.3*x1+tu;
    %模拟出u
    u=normrnd(0,1,n,1);
    y=0.5+2*x1+5*x2+u;
    %用得到的点（y,x1)来拟合，得到k来
    k=(n*sum(y.*x1)-sum(y)*sum(x1))/(n*sum(x1.*x1)-sum(x1)*sum(x1));
    K(i,1)=k;
    %求出x1与u'(u1)之间的相关性
    %先求出u1来，u1因为包含了y=0.5+2x1+5x2+u中的x2和u，所以按下面计算
    u1=u+x2;
    tr=corrcoef(x1,u1);
    r=tr(2,1);
    R(i,1)=r;
end
plot(R,K);
ylabel("K");
xlabel("R");

 

　　　　　弱化内生性条件：

 　　　　　　

 

 

对于回归系数的解释：

　　

 　　

 　　　　如下面的例子：

　　

 　　

 

　　

　　对特殊方程的解释：

 　　

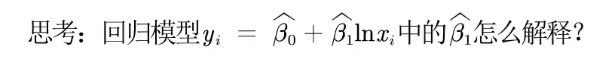
　　　我们什么时候对自变量取对数？

 　　

 

　　

 

　　

 　　

 

 当自变量为定性变量，我们该如何处理？

　　

 　　

　　   通常处理方法是：

　　　　将这个定性变量变成定量变量 （比如根据这个定性值是否出现定量成0/1）

　　　　然后再在这个定量变量前*一个系数

　　　　

 

 

　　　　

 使用stata工具完成回归：

　　

 　　

 　　部分数据：

 　　

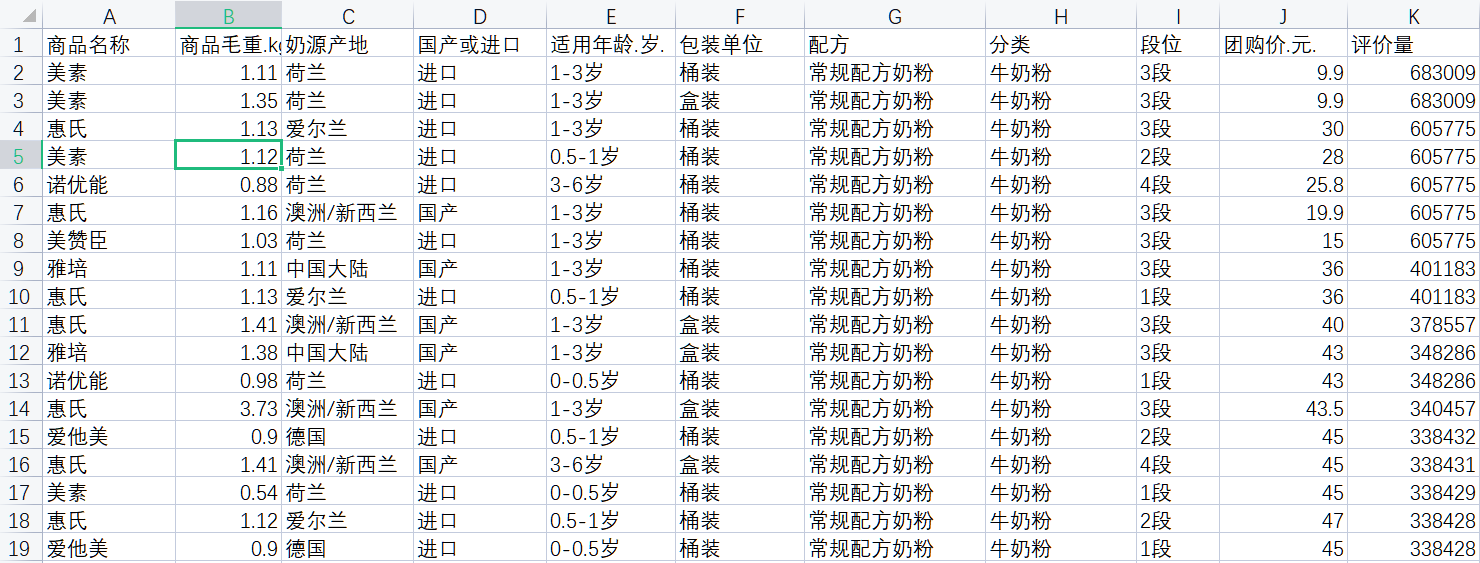
 　　1）

　　　　分析其他变量和评价量之间的关系

 　　　　　 那么首先就是要分析一下，其他变量与评价量是否有关系？（即相关性，具体看如何求解回归系数和回归系数的显著性）

　　　　 如果有关系，那么其他变量是如何影响评价量的？（具体看对于回归系数的解释）

　　　　 如果我们要在matlab中求解那么太复杂了，stata神器一键完成！<----

　　　　

　　　    首先，对于数据我们要分清楚什么是定量数据，什么是定性数据

 　　　　

　　 

 

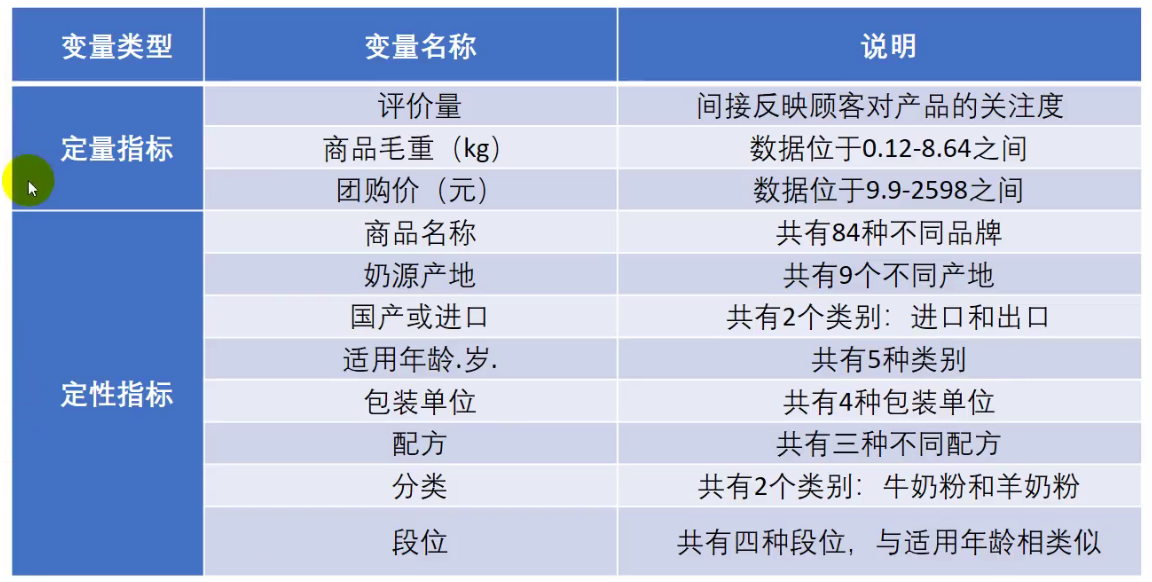
　　了解之后，我们要对数据进行处理：

　　　  处理定量数据：summarize 定量变量1 定量变量2 定量变量3....定量变量n

 　　　　  之后会返回一张描述性统计表,当然这张表可以加入到我们的论文中：

　　　　

 　　　　

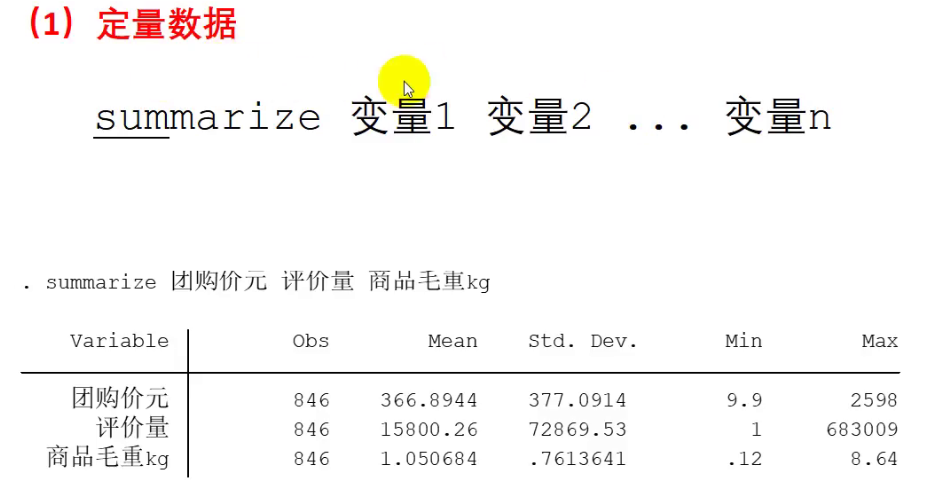
　　　　其中Obs为观测数（即样本容量），Mean均值，Std.Dev 标准差

　　　其实上述表格可以不用管，只要加到论文中即可

　　　　

　　　　在处理定性数据： tabulate 变量名，gen(A)

　　　这里gen(A)操作是给定性变量附上虚拟变量，然后返回一张频率分布表：

　　　　

 　　　　

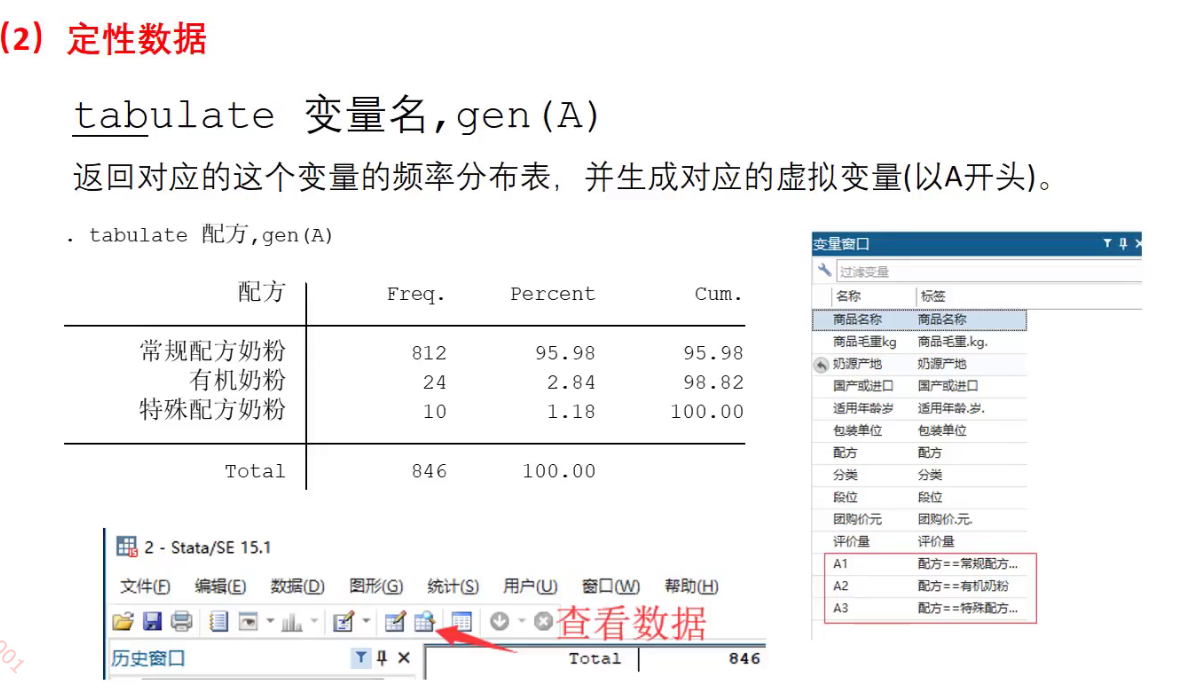
 　　　　Cum.是累加频率：即从上到下，频率的累加和

　　　

　　   然后开始回归：

 　　　　　　

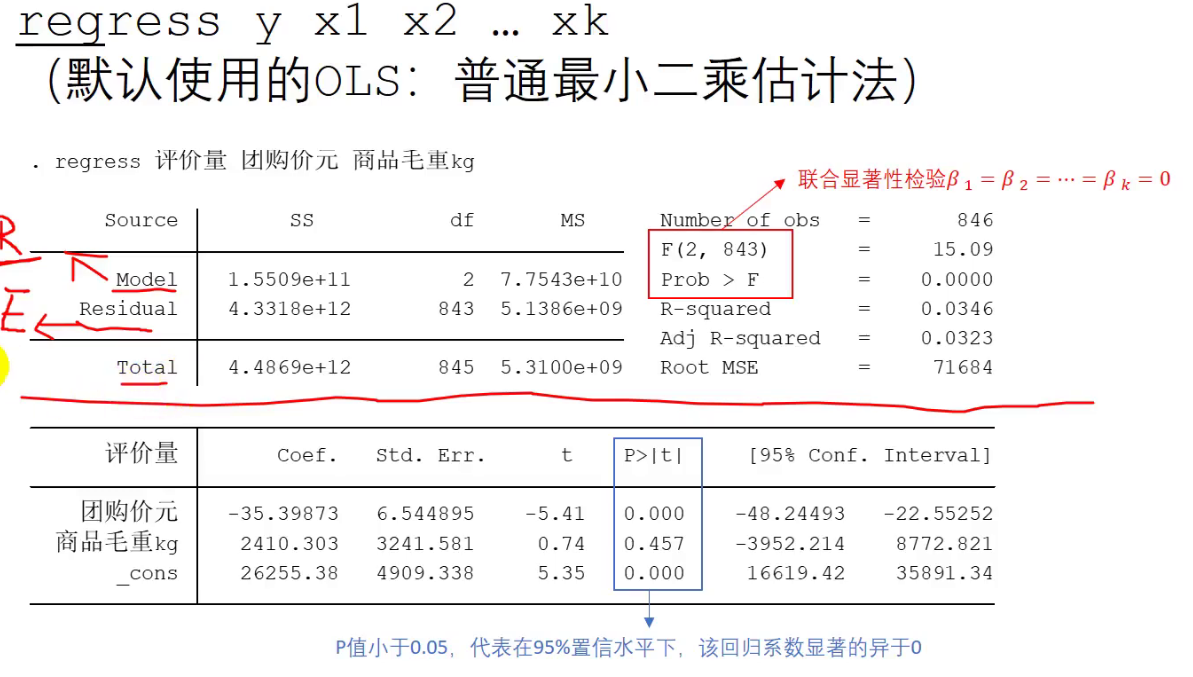
　　　　　　　　上述这张表中最重要的指标是：

　　　　　　Prob > F 其是P值，我们要看其是否<0.05,如果<0.05 说明我们这个对于评价量（y）构造出来的方程

　　　　　　通过了联合显著性检验在95%的置性区间下

　　　　　　否则没通过，这个方程都不能用

　　　　　　 R-squared是R^2，即拟合优度

　　　　　　 Adj R-squared是调整后的拟合优度

　　　　　　Coef是回归系数

　　　　　　P>|t|是P值，是对回归系数的显著性的P值，如果P值<0.05,则在95%的置性区间下，回归系数显著异于0，可以用

　　　　　　[95% Conf. Interval]是回归系数95%的置性区间

 

 

 

 　　　　　　使用的时候我们可以一口气将解释变量x全部写上：

 　　　　　　　　

 　　　　　　　　这里reg是regress的简写

　　　　 其中A1 B1等是虚拟变量

　　　　 需要注意的是当对虚拟变量进行回归时，会有一个虚拟变量如：

　　　　　　对A虚拟变量进行回归，其中有A1 A2 A3 A4 ，会有一个作为对照量，如A4,

　　　　　　这是为了完全多重共线性的影响

 　　　　　　　　

　　　　　　　　

 　　　　　　

 　　　　

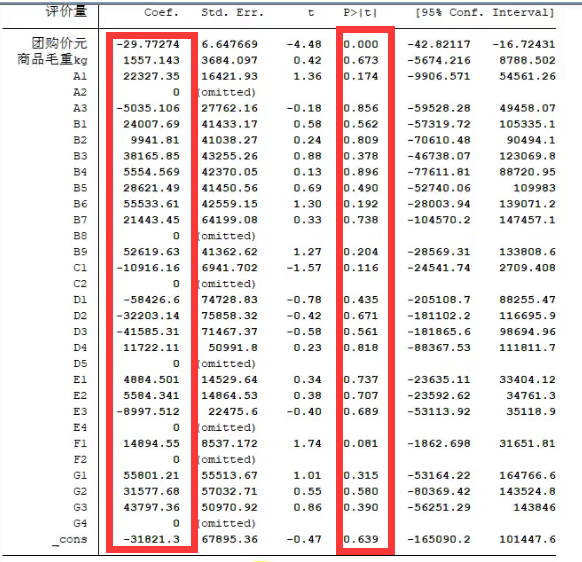
 　　　　然后就是找显著的，他就是对评价量有关系的

 　　　　

 

　　2）　　 

　　　　

 　　

 　　

 　　　　

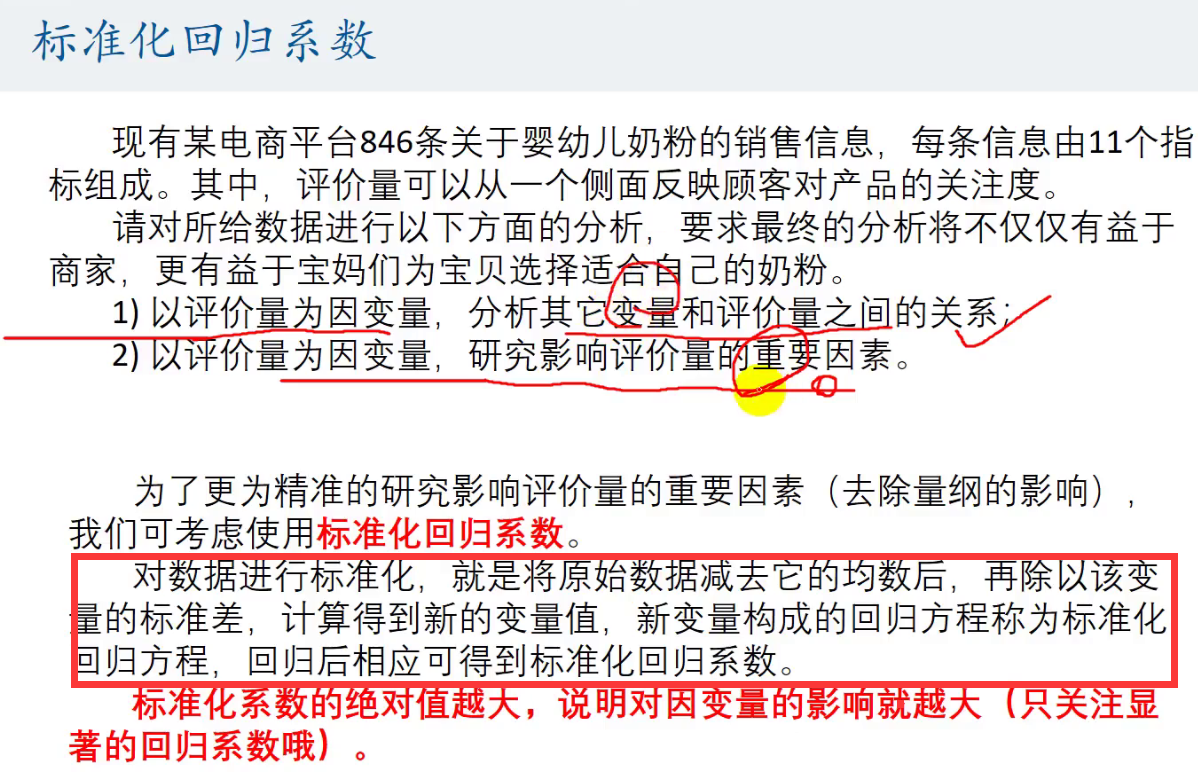
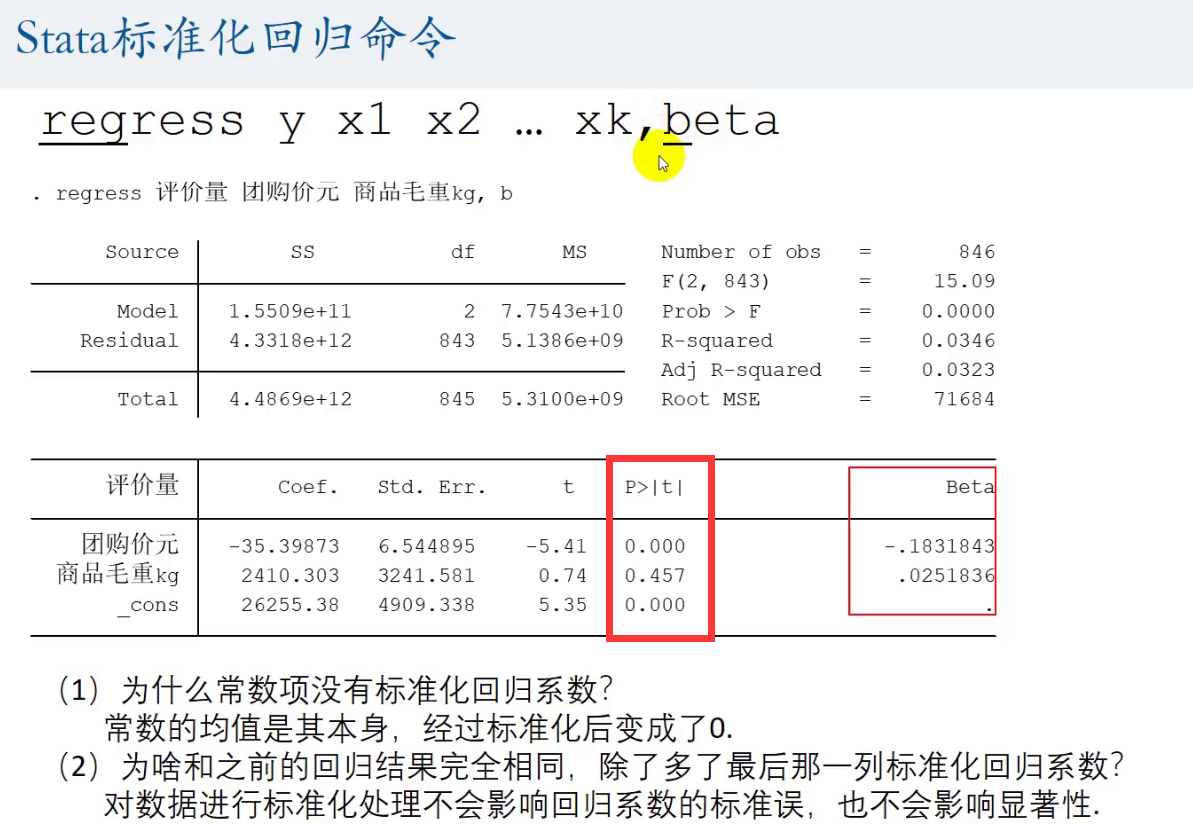
 　　　　还是首先看P值，看是否<0.05 ，即就是看回归系数是否显著

　　     然后再看Beta的绝对值，Beta就是标准化系数

 

 

 

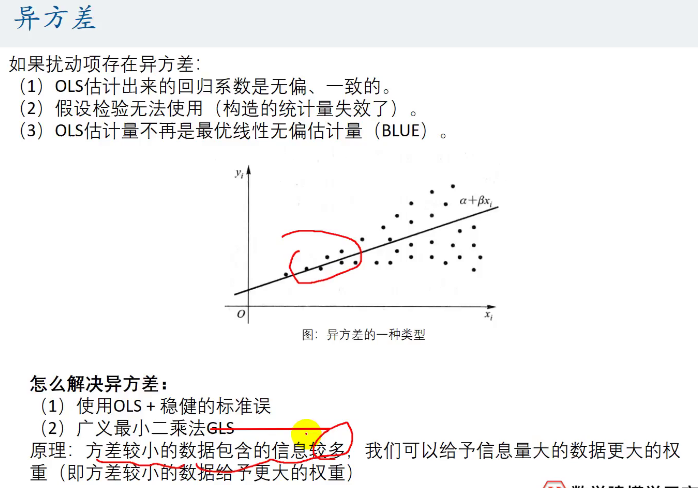
回归完后进行异方差检验：

 　　

 

　　　　

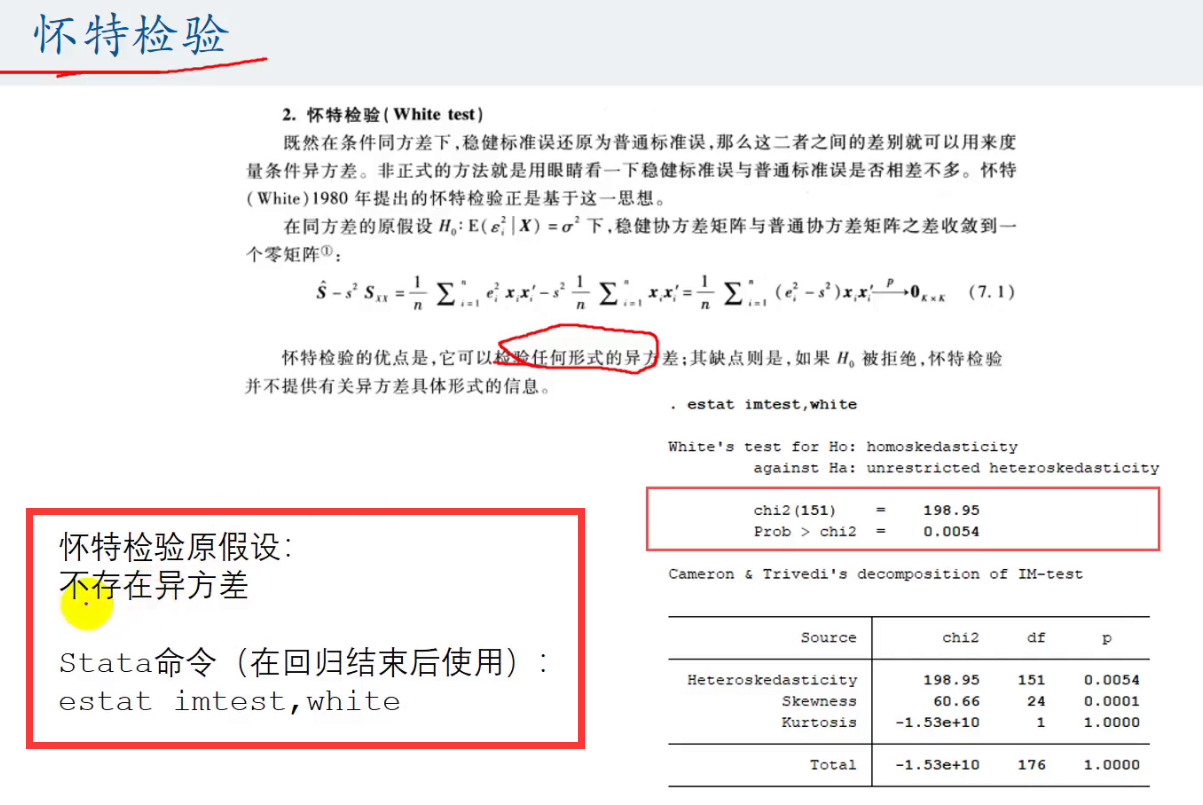
 　　即看我们的P值有没有<0.05 （这里的P值是 Prob>chi2）

　   如果小于则我们在95%的置信区间内无法拒绝原假设，

　　这里即是不存在异方差

　　

如果检测出来了异方差也不要害怕，使用下面的方法解决异方差：

　　

 

 

 

 

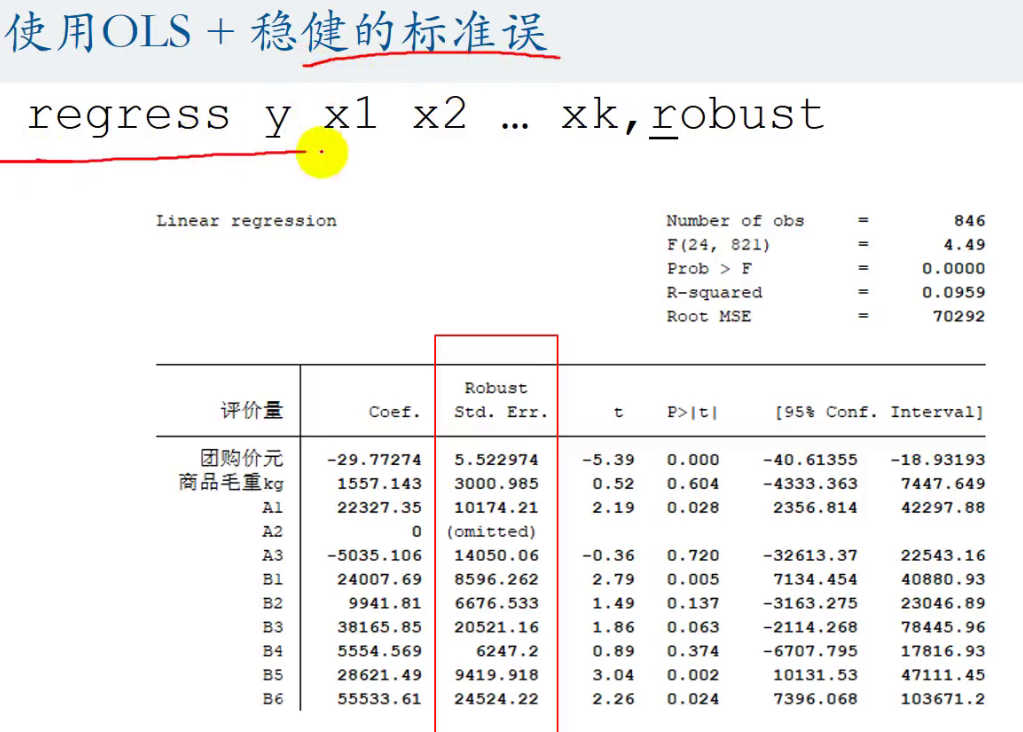
回归完后进行多重共线性的检验

 　　

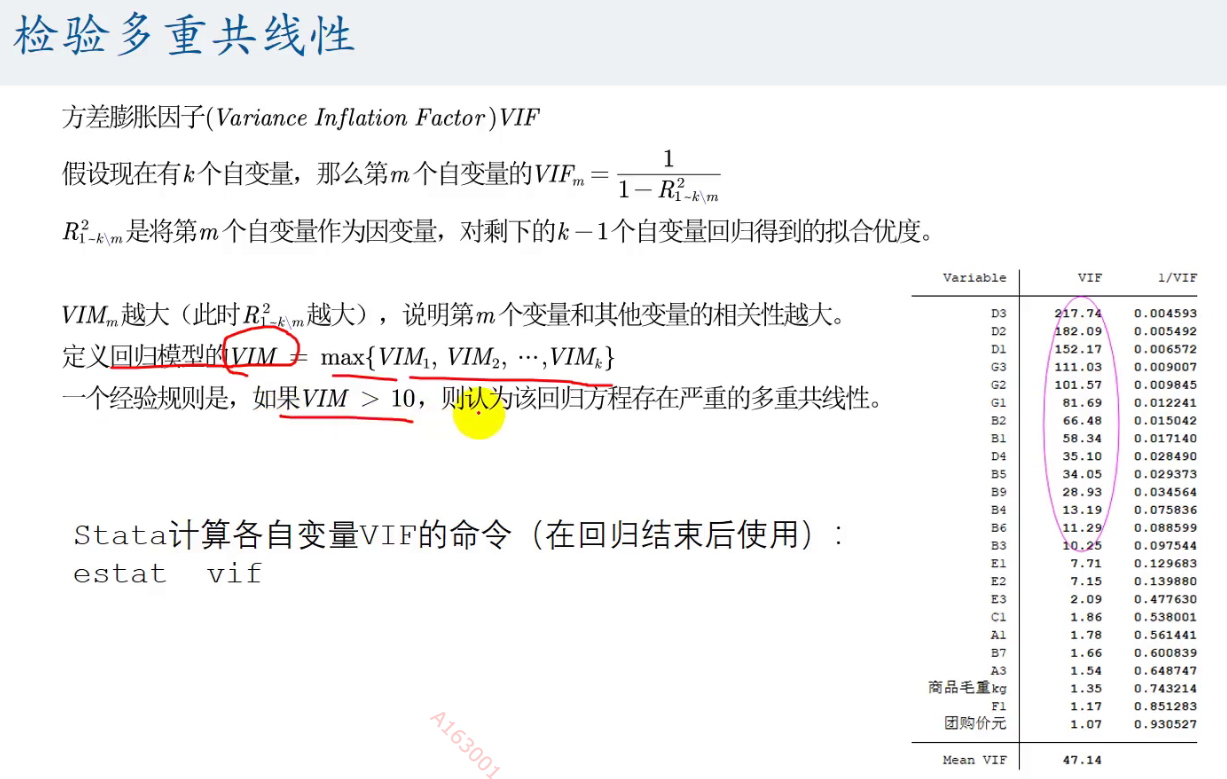
 　　可以看到我们上面的变量出现了多重共线性的问题

　   如何解决呢？

　　

 　　

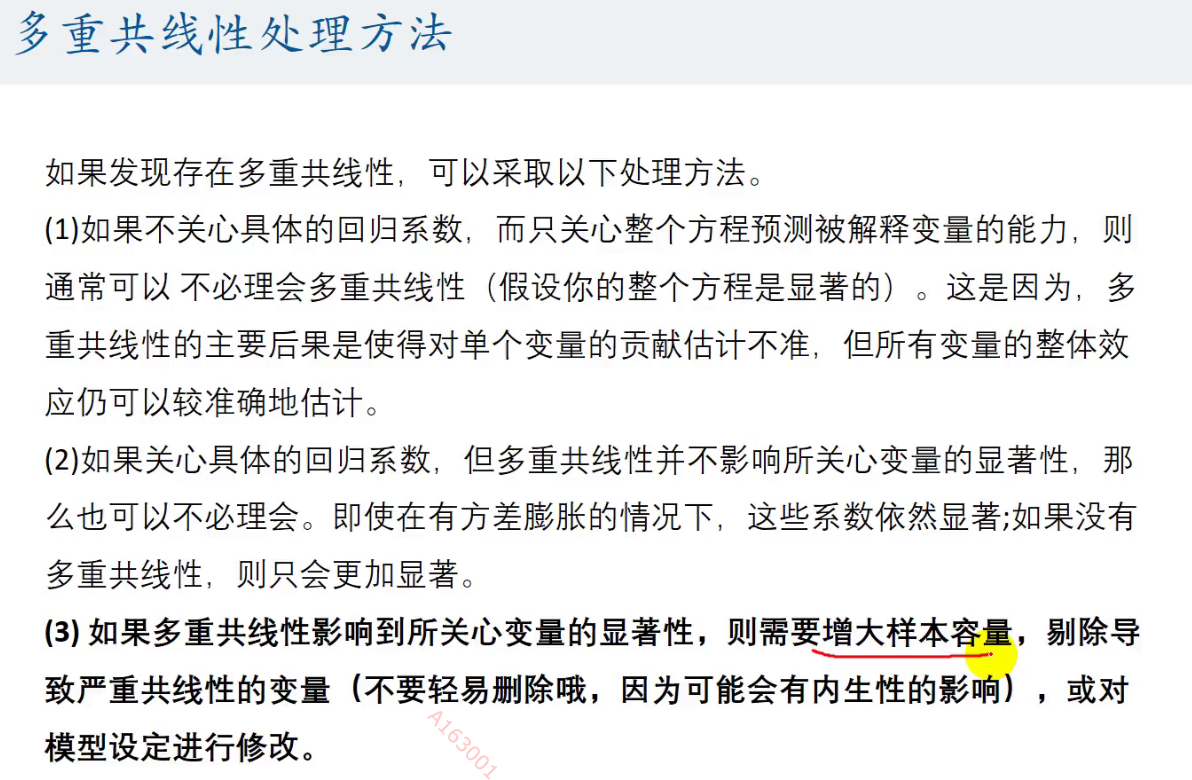
 　　上面只是说说的，在数学建模中出现了多重共线性的问题后

 

　　我们可以使用逐步回归分析的方法解决：推荐使用向后逐步回归

 　　

 

 　　

 

 　　　　

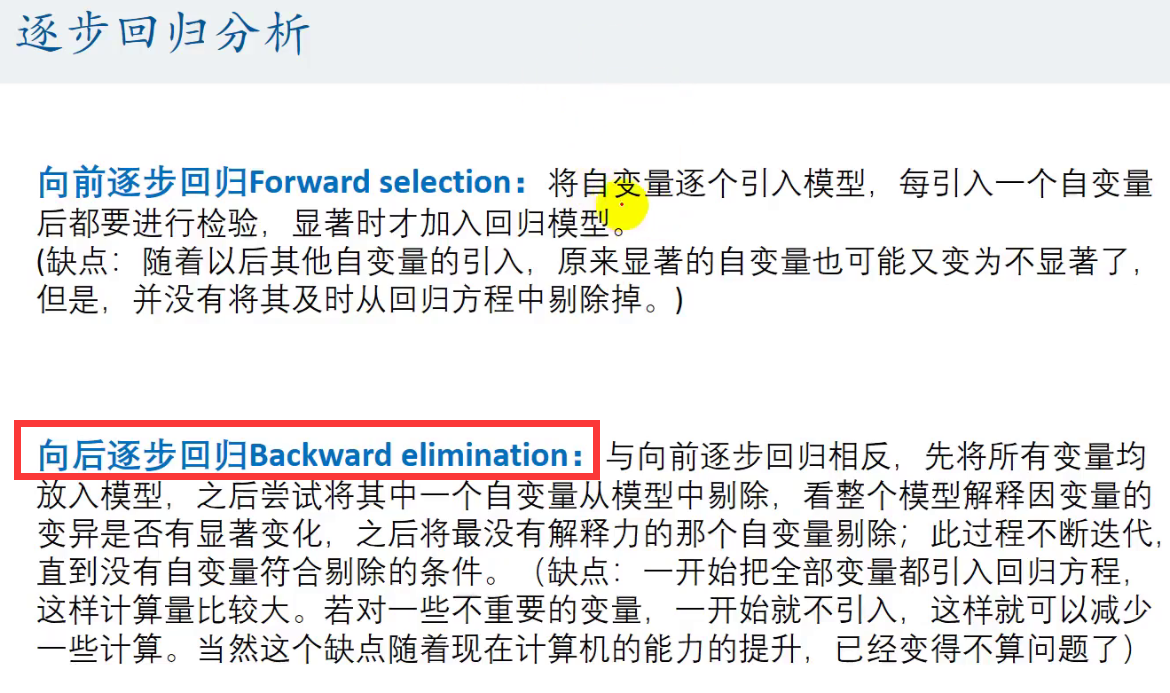
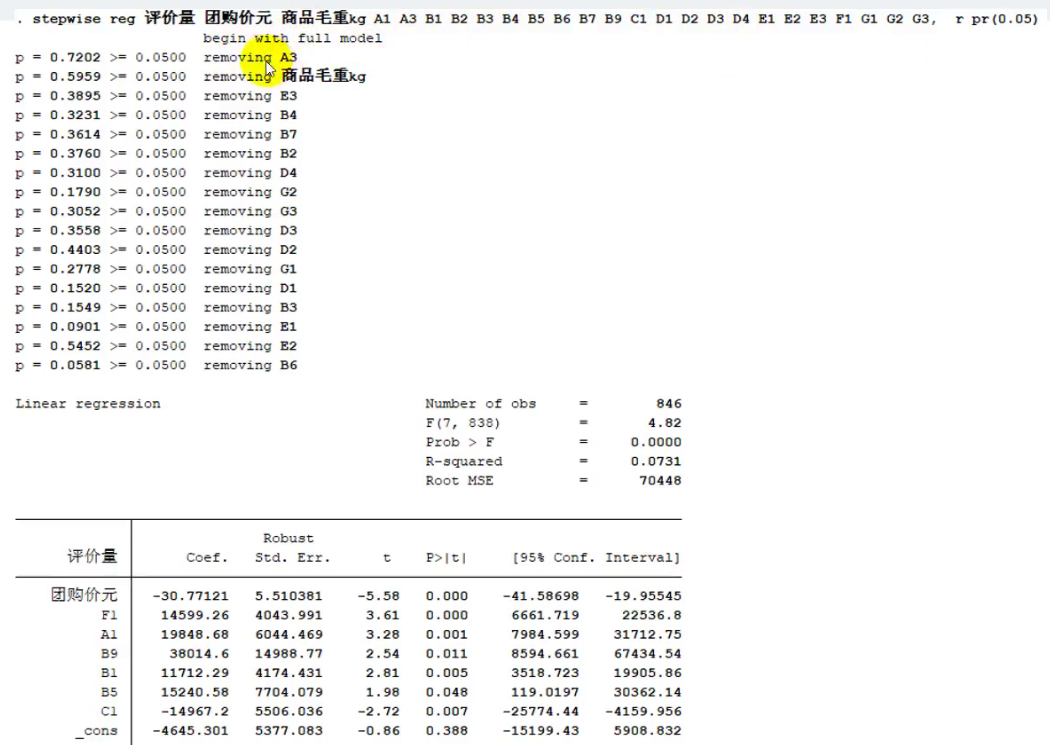
 　　　　这个#2是我们的α