数学建模----相关性模型

 

皮尔逊person相关系数

　　总体皮尔逊person相关系数

 　　

　　　　

　　样本皮尔逊相关系数

　　　　

 　　

 

　　　　　

　　　 使用皮尔逊person相关系数的前提和注意事项

　　

 　　  　

 

 　　　　

 　　　　

 

　　　　

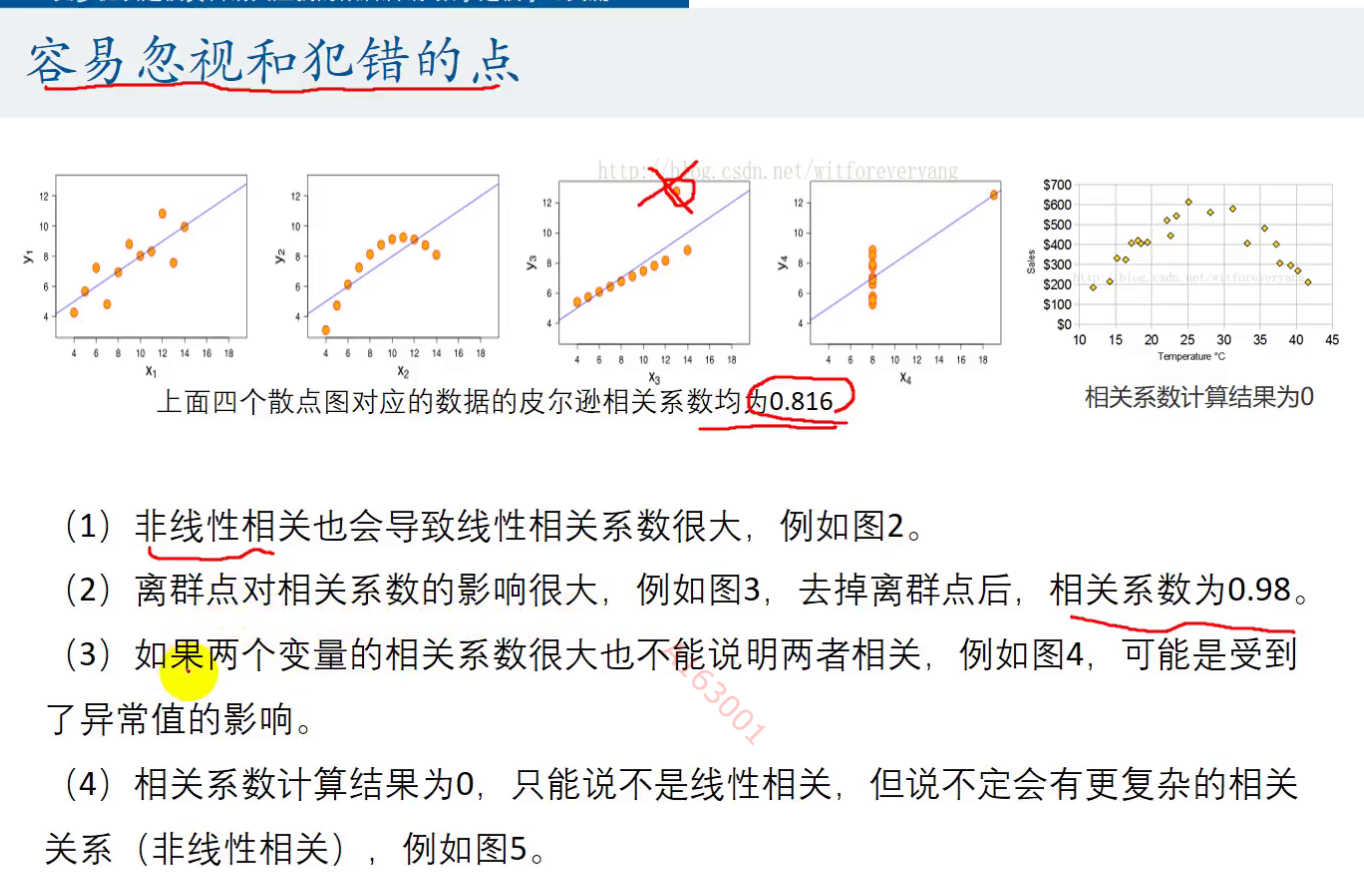
　　　　　　这个也就告诉我们，如果我们想要运用皮尔逊相关系数我们就需要首先确定其线性相关性

　　　　　　只有在确定了线性相关性后，相关系数才有意义

　　　　  如何确定？

 　　　　　　　　画出两两之间的散点图，然后根据散点图确定线性

　　　　　　y=kx+b

　　　　　　当k=无穷 或者 不是个线性时就不是线性相关

　　

 　　　　　　

 　　　　

　　　如何画出数据两两之间的散点图？　　

 　　　　

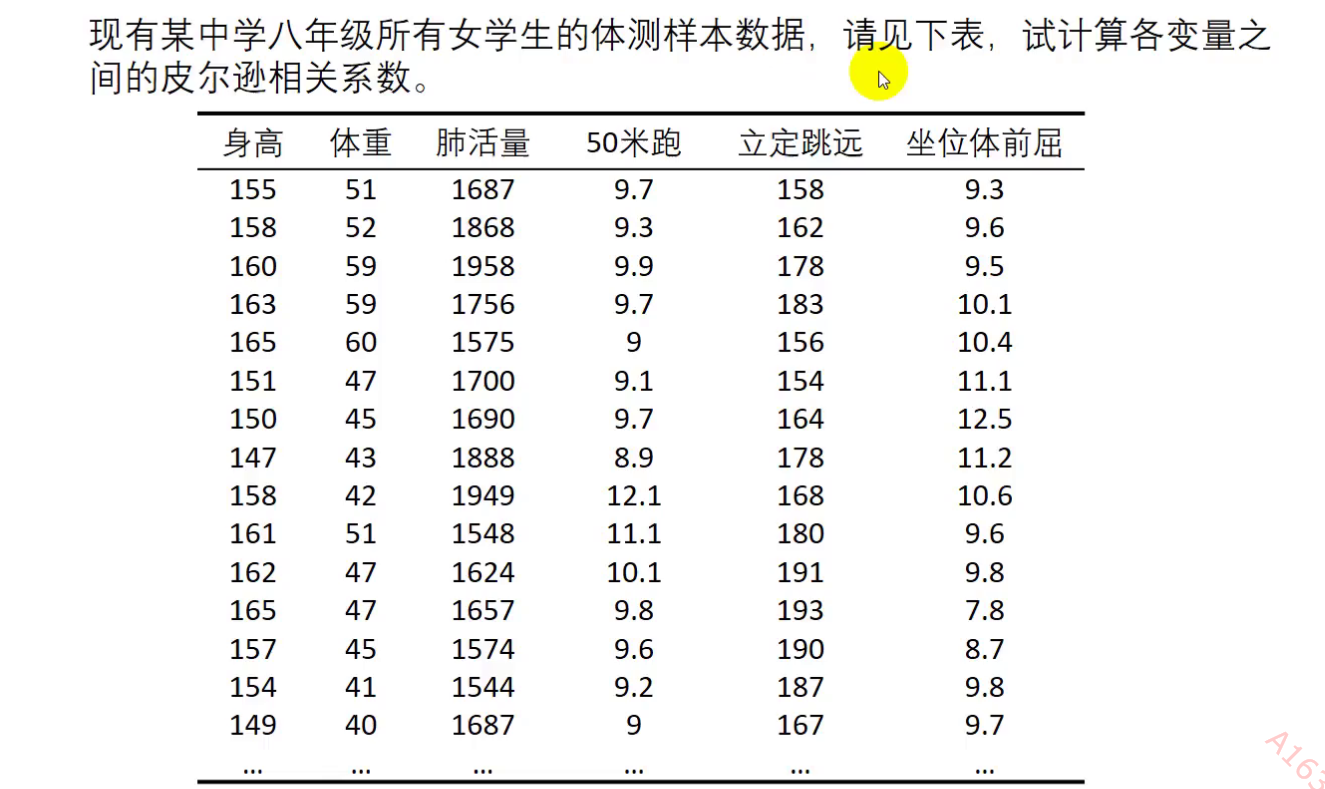
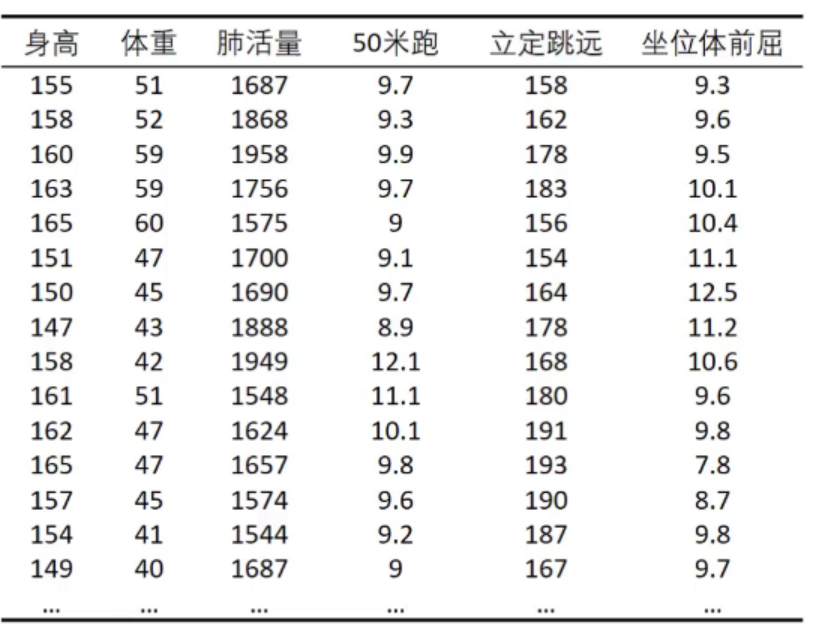
　　　　　　如我们有这样一个例题：

　　　　　　问身高，体重......,坐位体前屈 之间有何关系？

　　　　　　这也就是在问他们之间的相关性

　　　　　　

　　　　 我们要画出他们两两之间的散点图，用SPSS这个软件

　　　　

 　　　　 　　

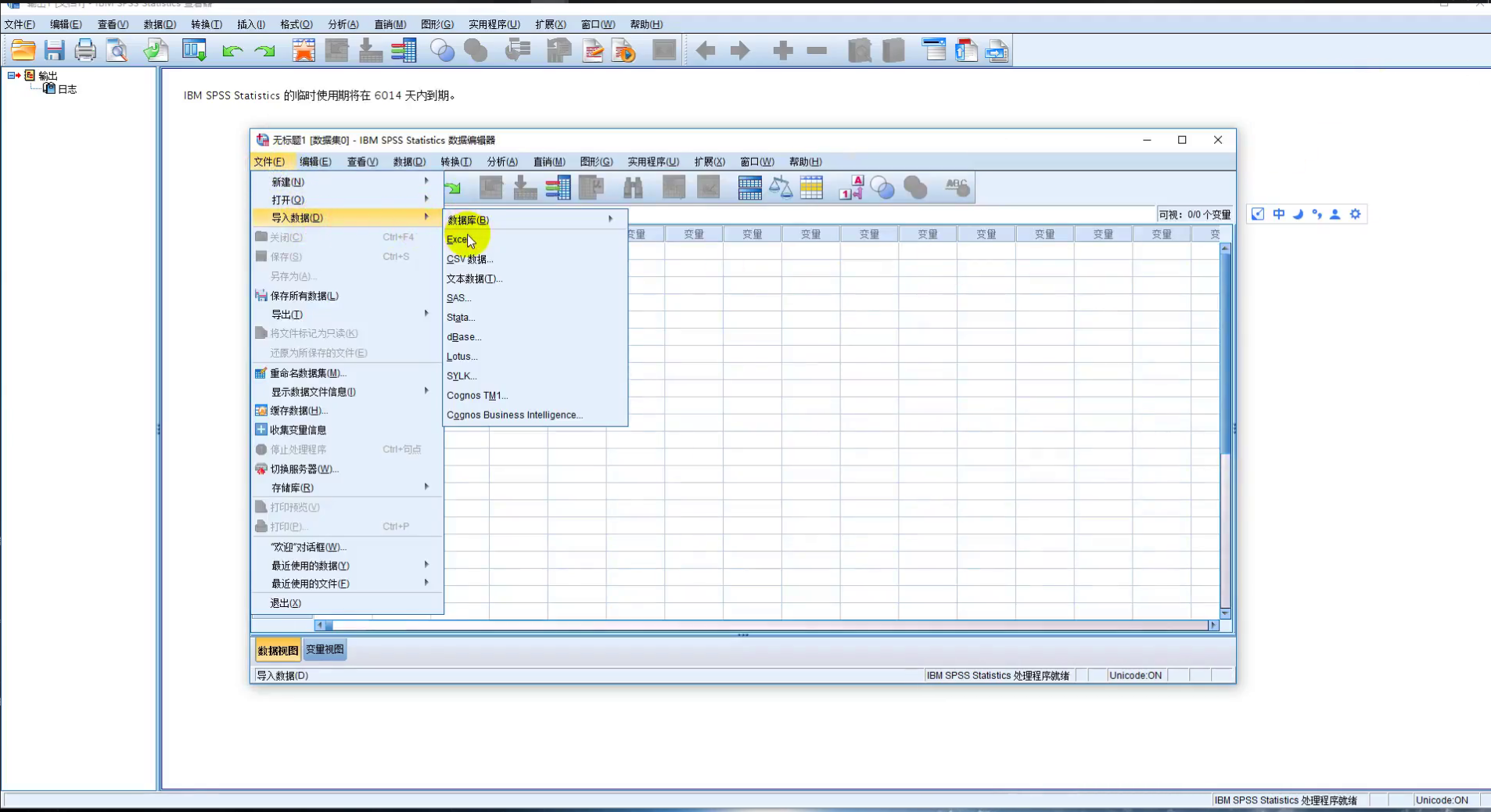
 　　　　　　我们将上面数据导入进去

　　　　

 　　　　　　

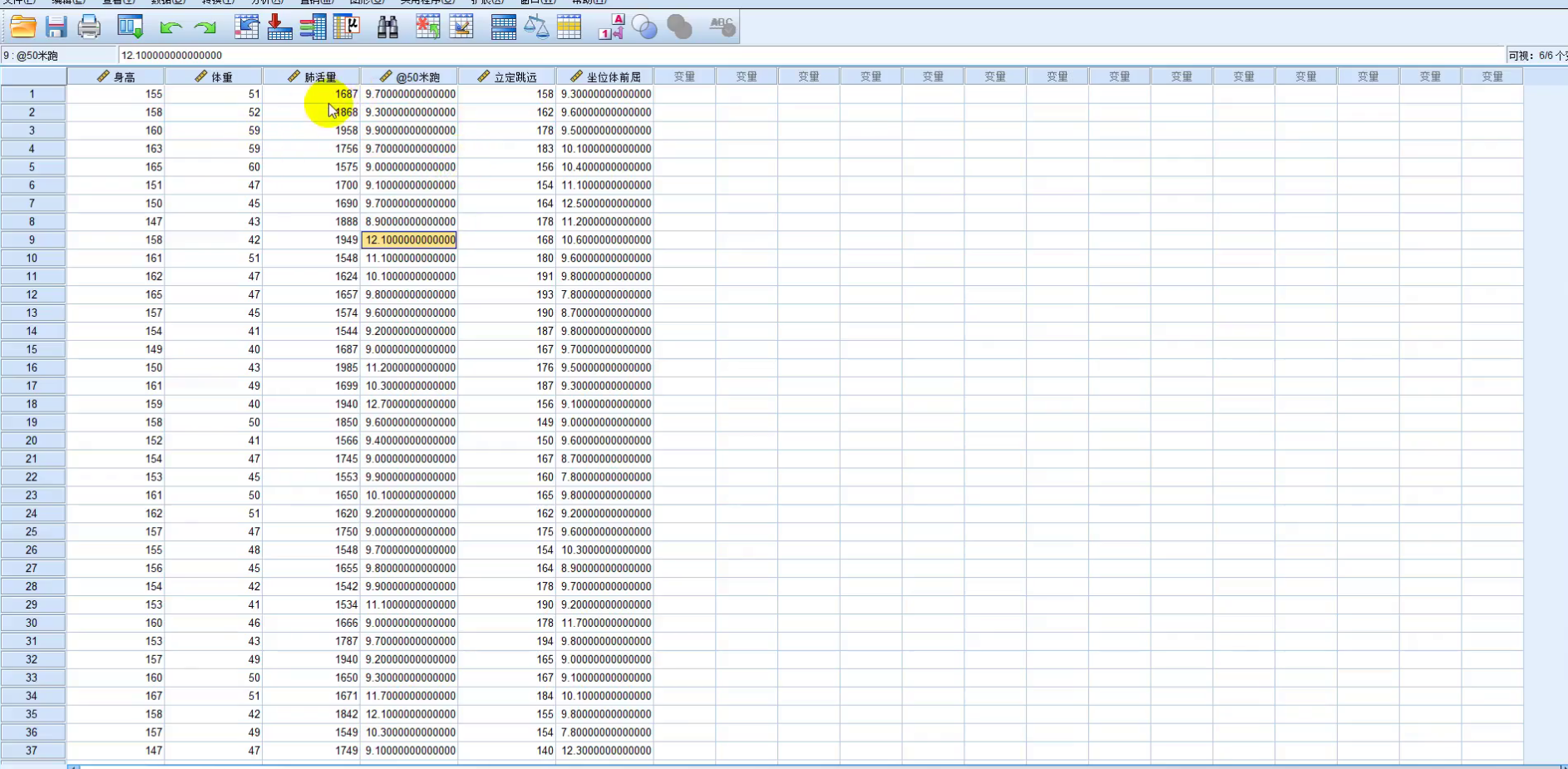
 　　　　　　导入后

　　　　

 　　　　　　

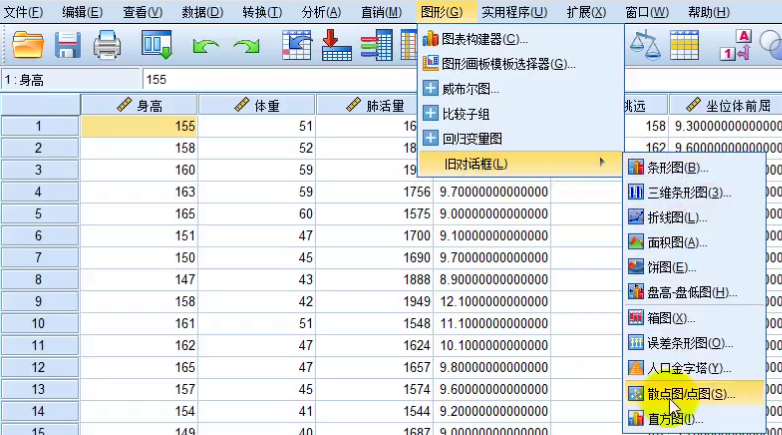
 　　　　　　点击矩阵散点图

　　　　

 　　　　　　

　　　　　　

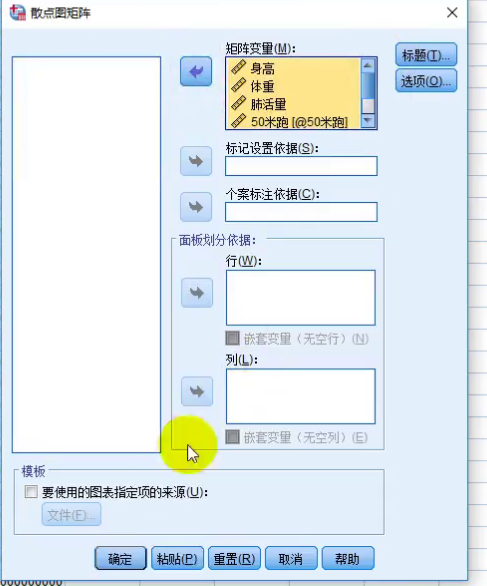
 　　　　　　得到

　　　　

 　　　　　　

 

 

　　计算皮尔逊相关系数

　　　　

 　　　

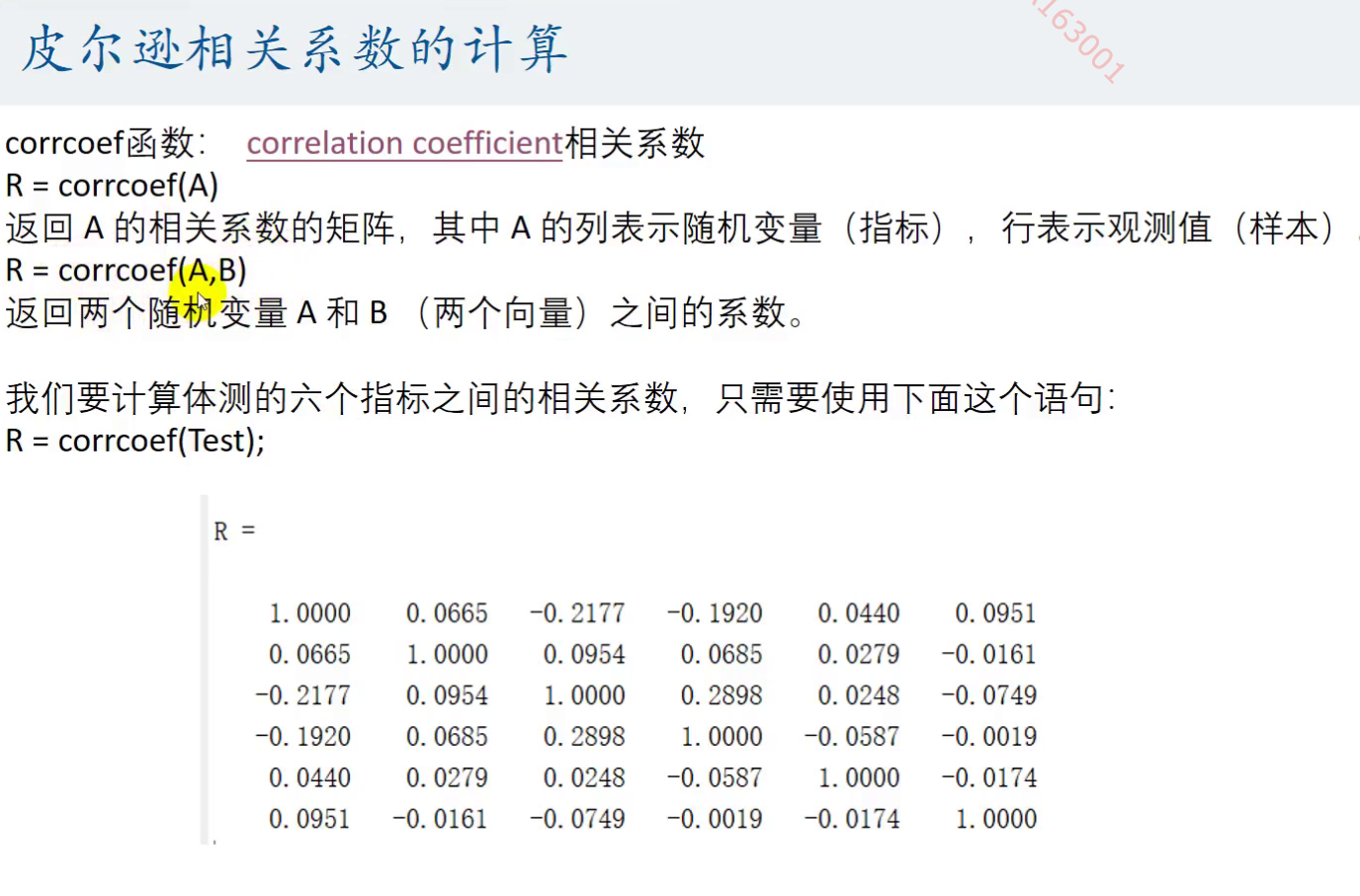
　　　这个A就是

 　　

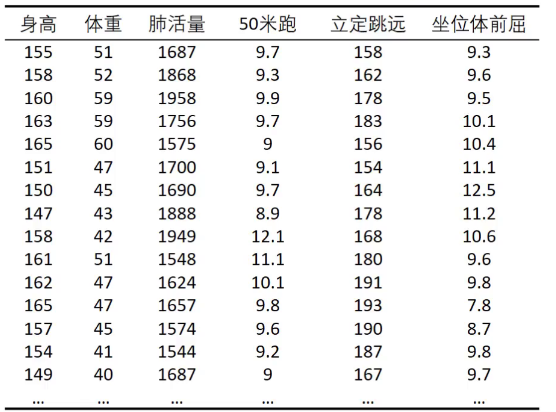
　　　　我们这些数据当成矩阵A，导入进去

　　　　得到的R的含义是如下：

　　　　

 　　　　

 　　　　

 

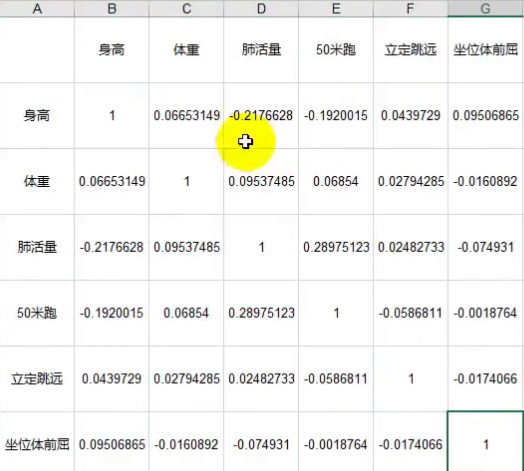
 　　数据可视化

　　　　

 　　

 　　我们想要达到上面图片的效果，那么可以在Excel工具中如下：

 　　

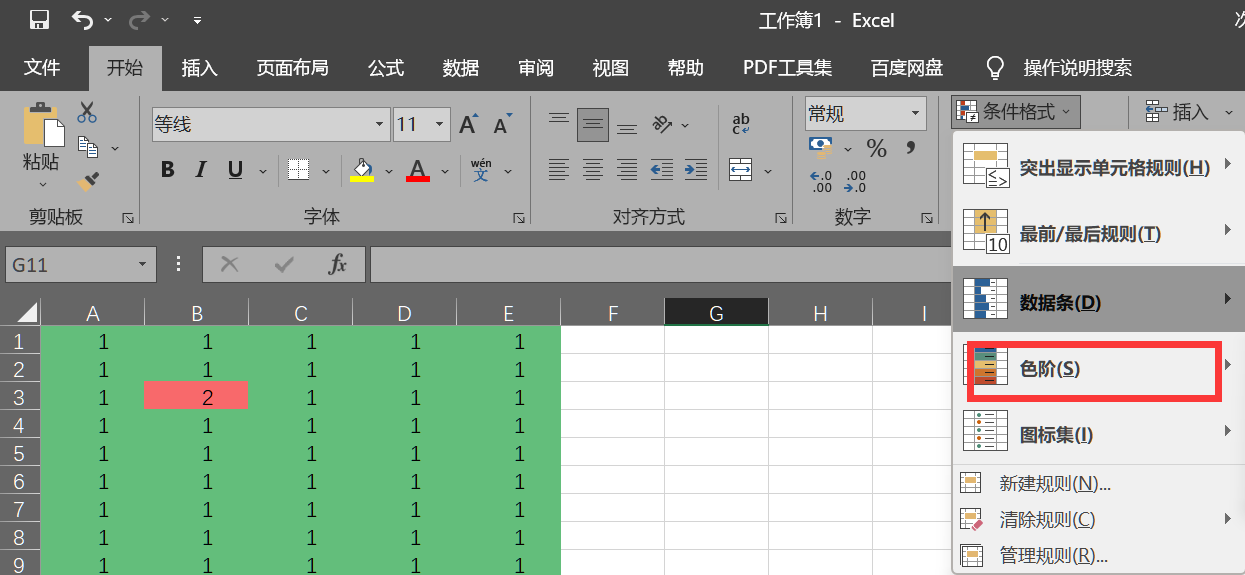
 　　在其他规则中设置参数，变得更加美观：

 　　　　

 

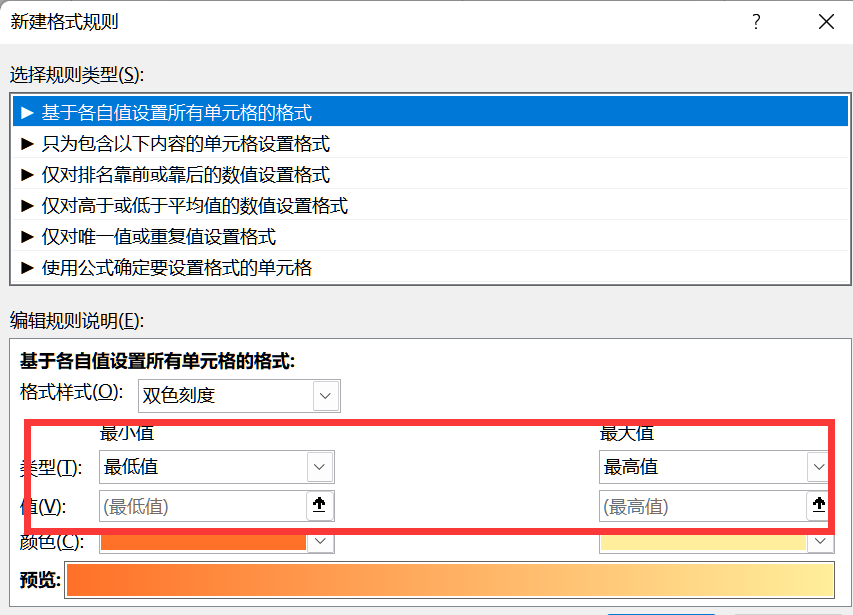
　　对相关系数进行假设检验　　　

　　　　当我们的相关系数计算出来时，我们需要对相关系数进行假设检验

　　　　看相关系数是否显著异于0

　　　　如果不显著异于0，那么相关系数也无法被接受

　　　　

 　　　　

 

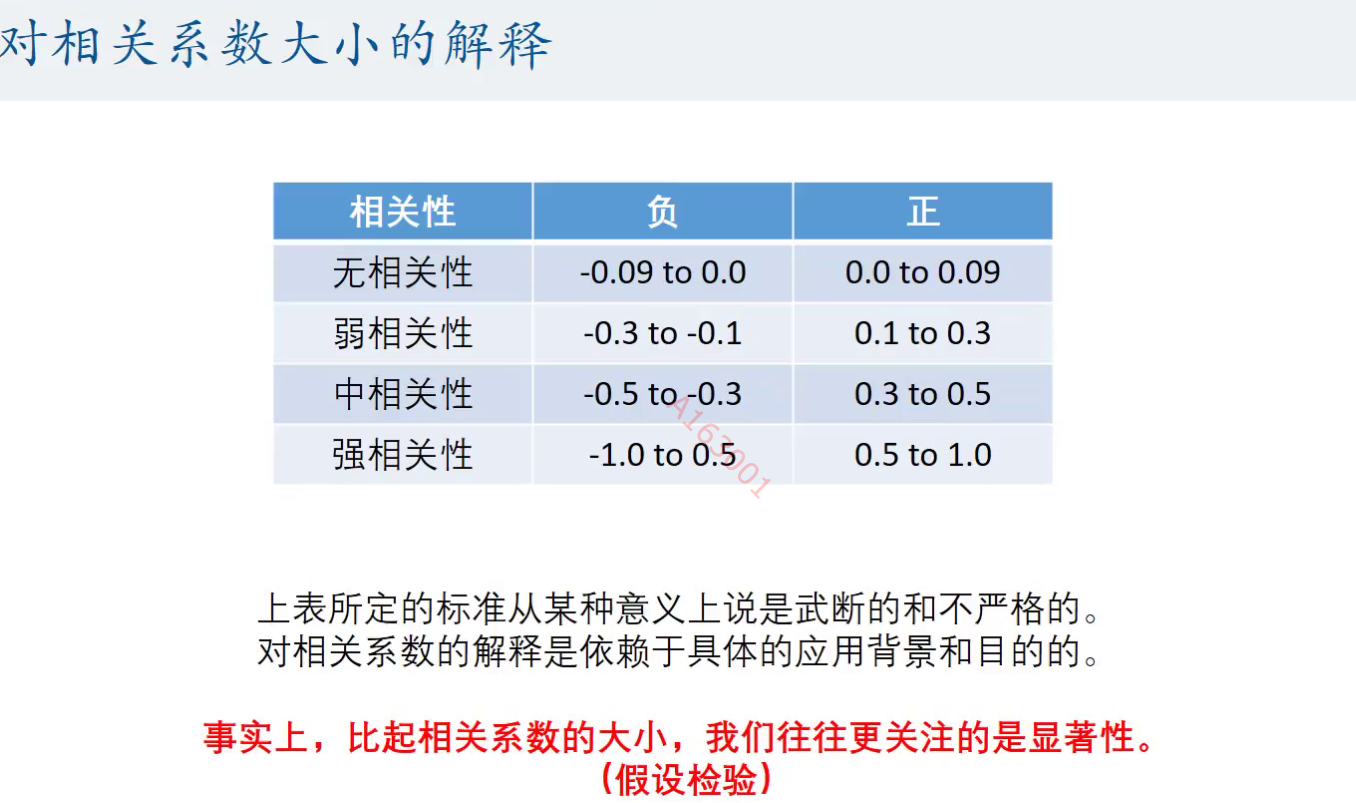
　　相关系数假设检验的步骤：

　　　　　　　　进行假设检验的前提：

 　　　　　　　　

　　　　　　针对大样本检验的正态分布JB检验:

　　　　　　　　注意其是个大样本检验

 　　　　　　　　

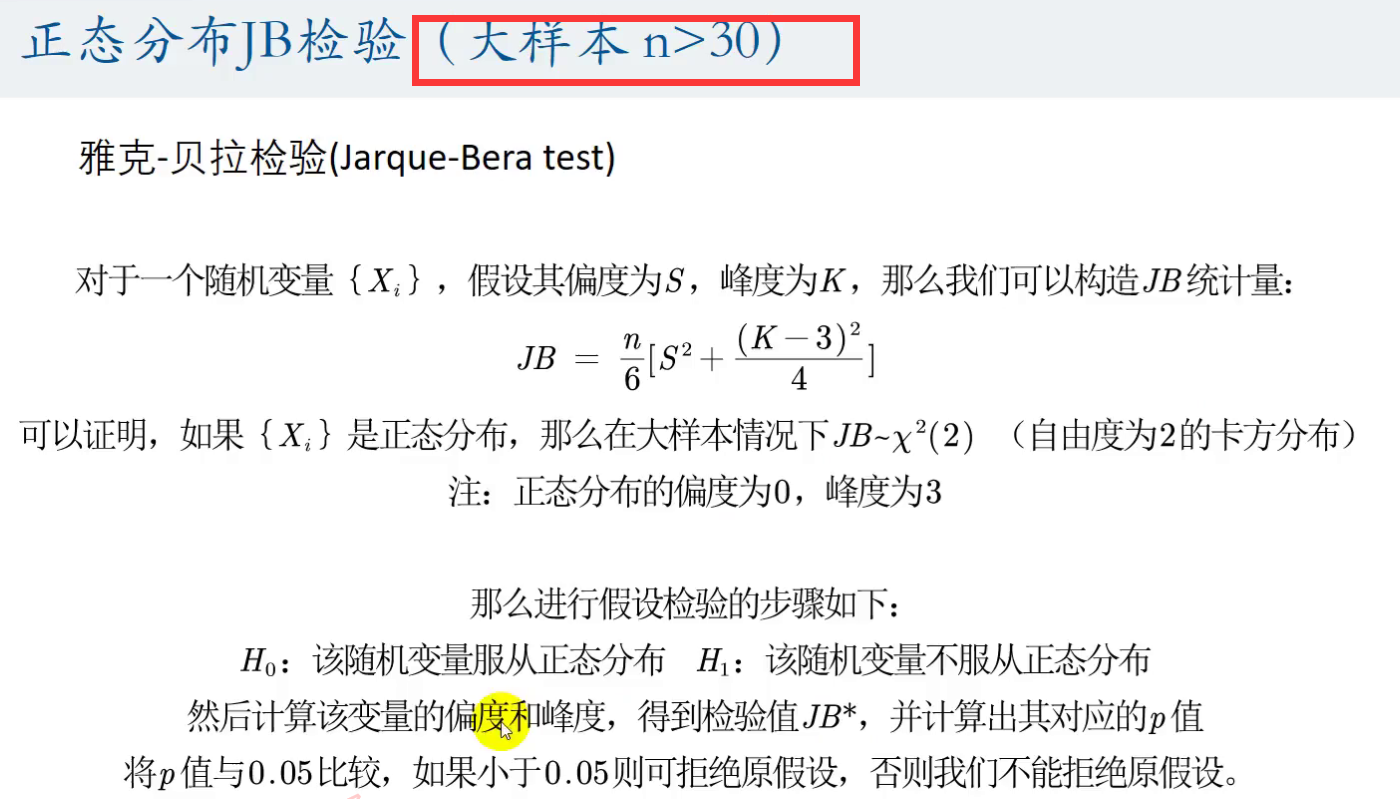
 　　　　　　　　matlab中有相应的函数：

　　　　　　　　

 　　　　　　　　　　

 　　　　　　　　　　　　这里的p是我们的p值

　　　　　　

 　　　　　　　　　　　　

　　　　　　　　　　　　　　这个操作相当于对我们的矩阵进行初始化

 

　　　　　 对于小样本也可以进行检验的 Shapiro-wilk检验

 　　　　

 　　　　　　

 　　　　　　　　

 　　　　　　　　

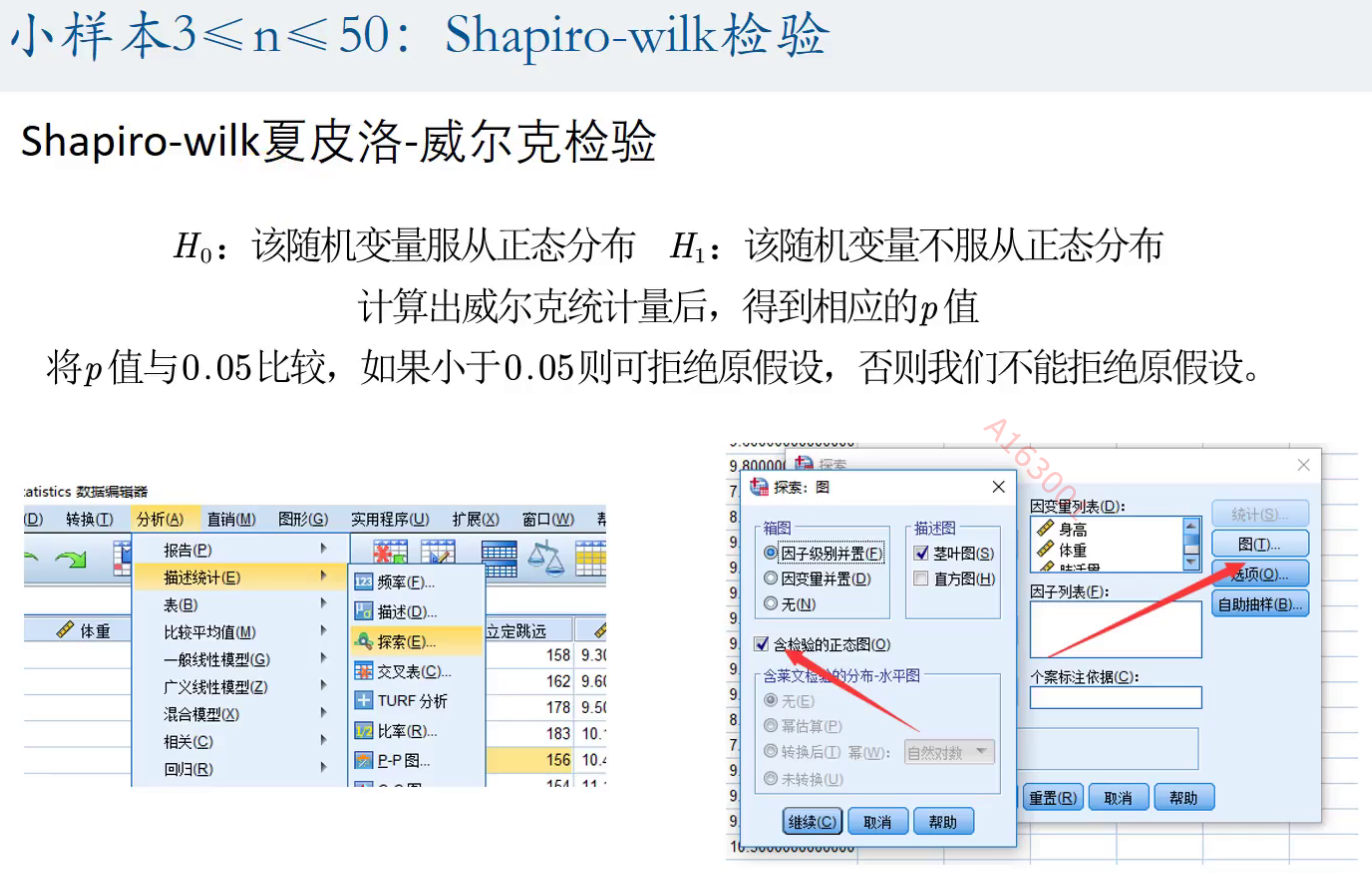
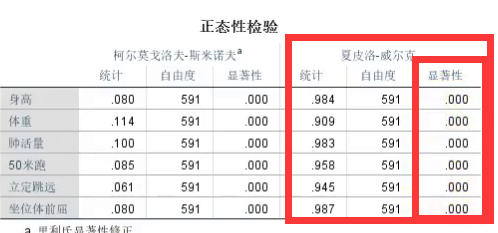
 　　　　　　　　这个显著性就是我们的p值，看其是否>0.05 如果大于那么这些数据是服从正态分布的

　　　　　　

 

　　　　　　　　　　

　　　　　　对数据检验完后的计算： 

 

　　　　　　　　

 　　

 　　　　　　

 　　　　

　　

　　　　

 　　　　

 

 　　　　　　

 　　　　

 

　　　　

 　　　　

 

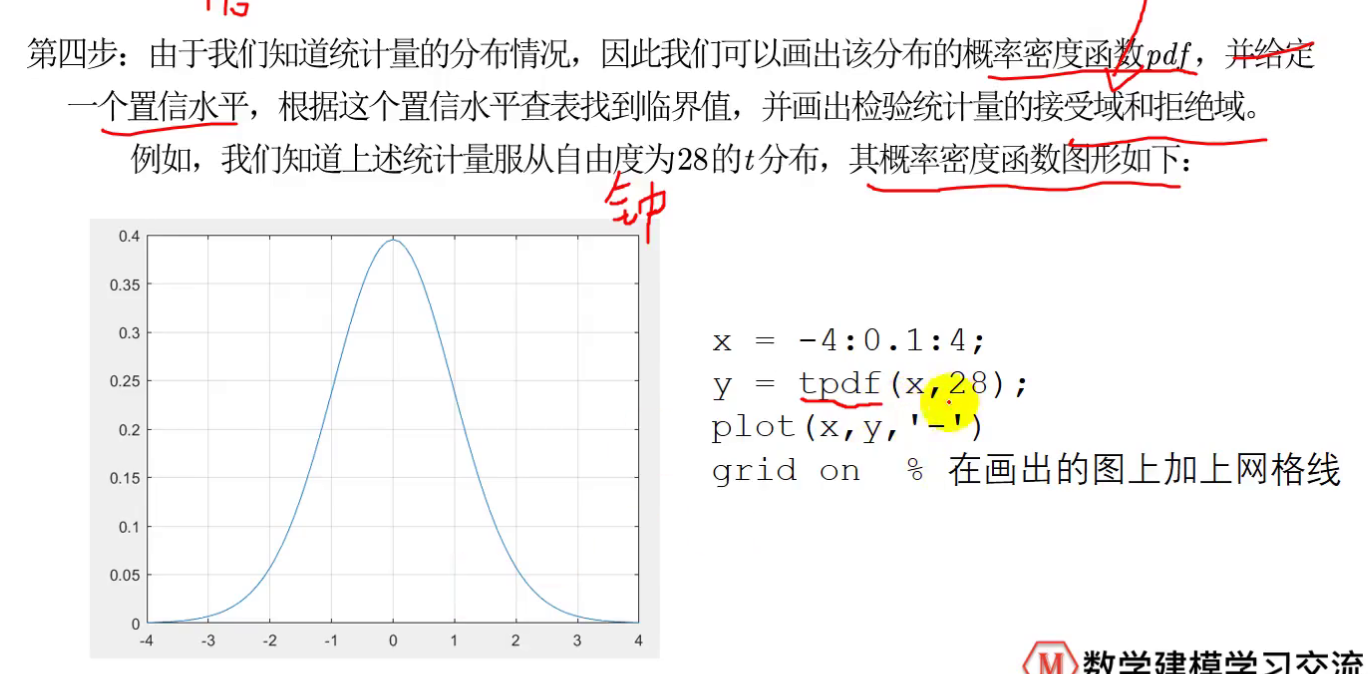
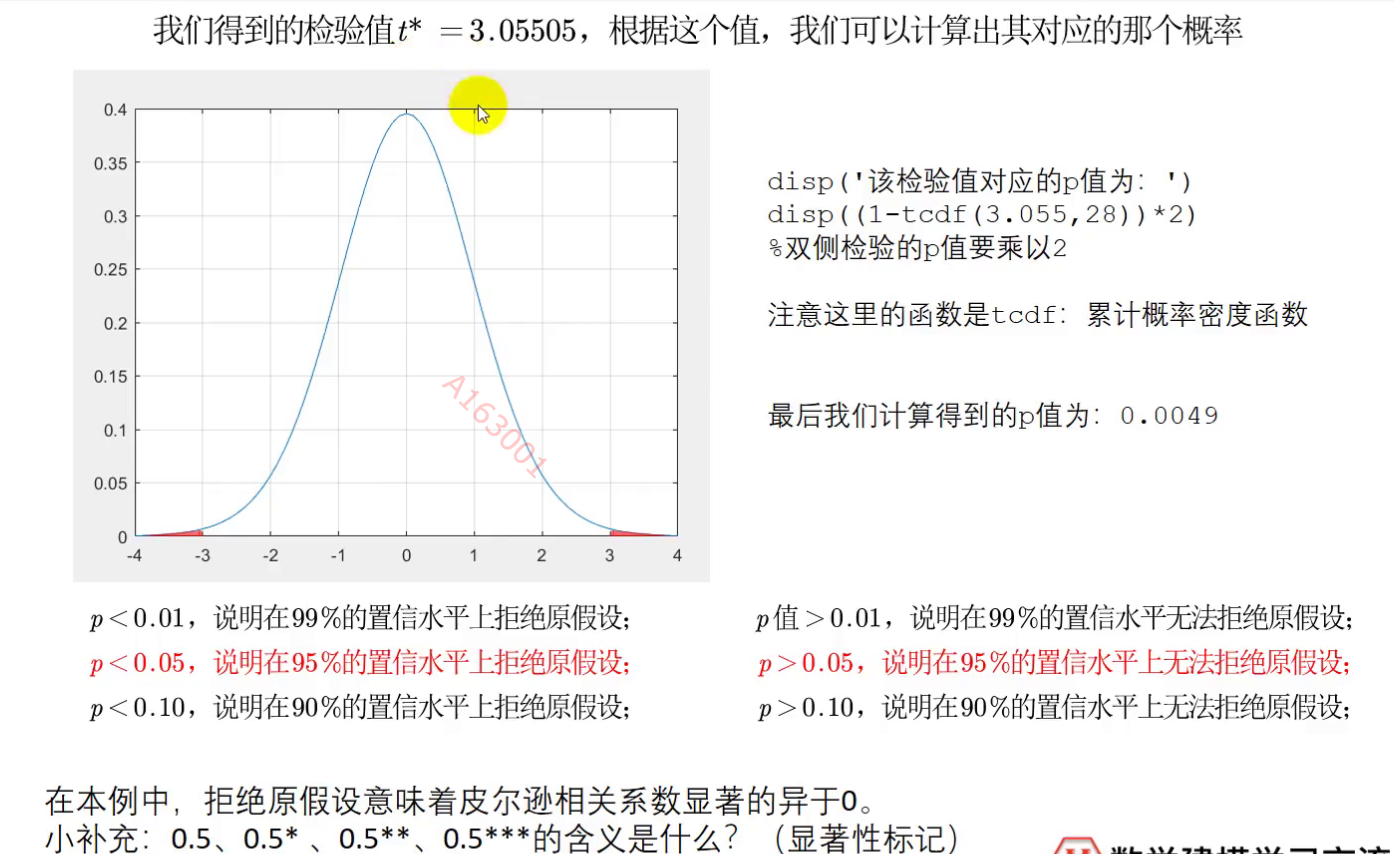
 　　　　　　这个*表示 在越大的置信水平下受到拒绝，那么*越多

　　　　   这个所谓的p值就是我们用t*计算出来的α

　　　　  这个可以用matlab进行计算：

　　　　　　　

 　　　　　　

　　　　　　

　　　　　　这里得到的P是一个矩阵，即两两之间相关系数的p值

　　　　  

　　　　　也可以用SPSS来计算：

　　　　　　

 　　　　

 

 　　　　

  　　

　　　

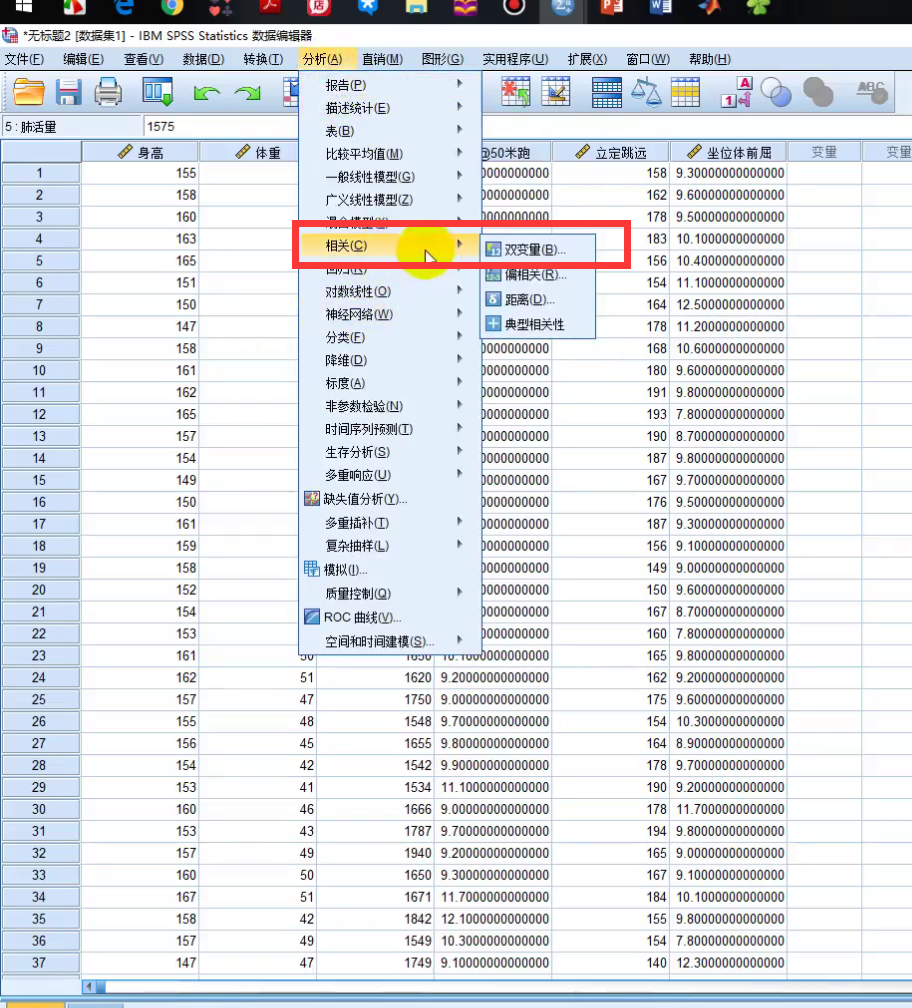
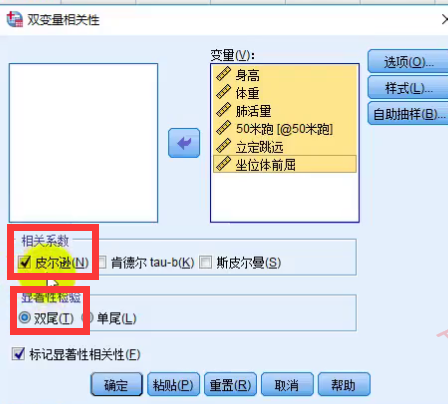
　　　matlab中关于假设检验要使用的函数：

　　　　下面的这些函数均是t分布的：

　　　　f(x)=tpdf(x,n-2)

 　　　　　　这里的tpdf中 n是自由度

　　　   

　　　　概率P=F(x)=tcdf(x,n-2)

　　　　 x=F-1(P)=tinv(P,n-2)

　　　　 上面 tinv 是 tcdf 的反函数

　　　　

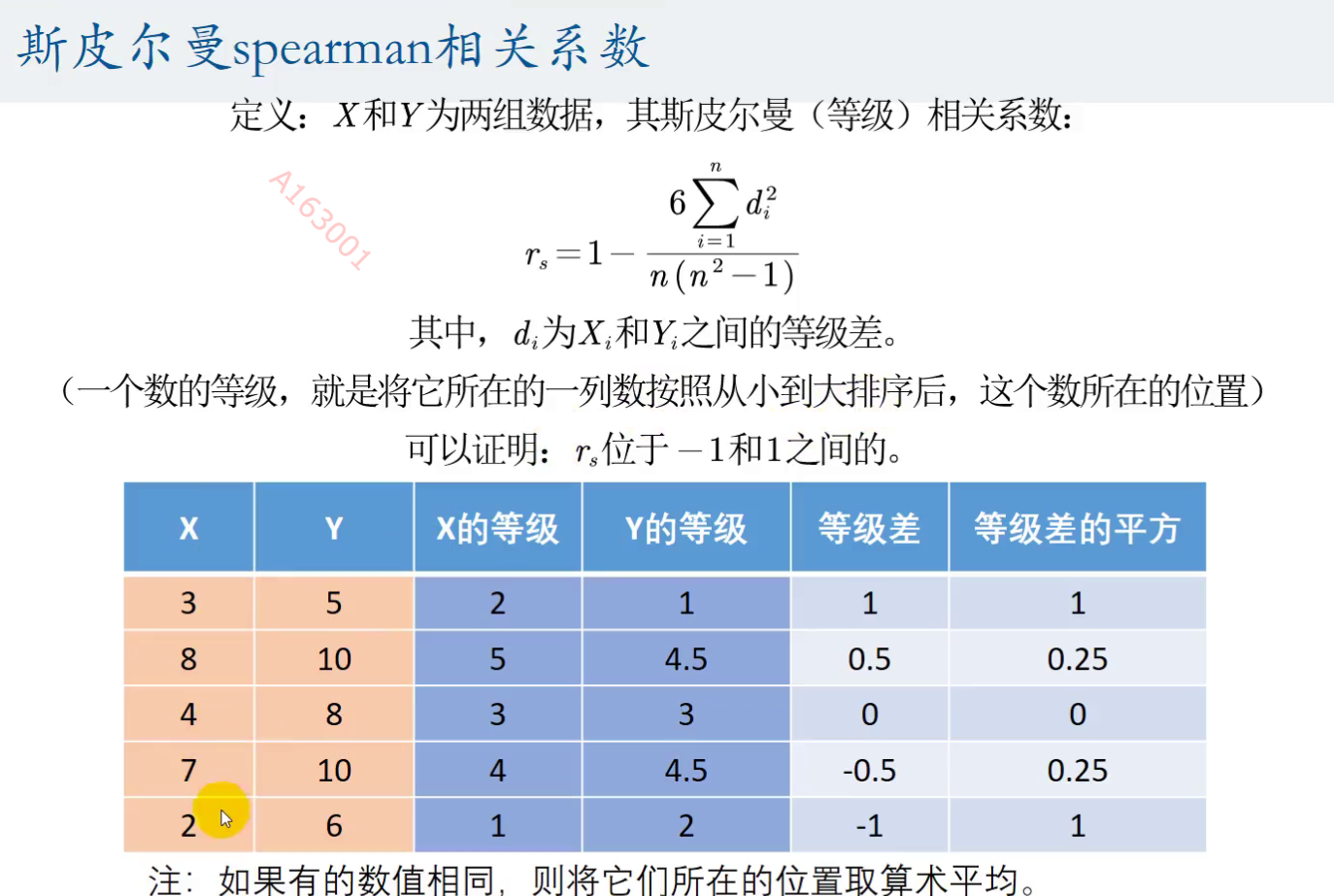
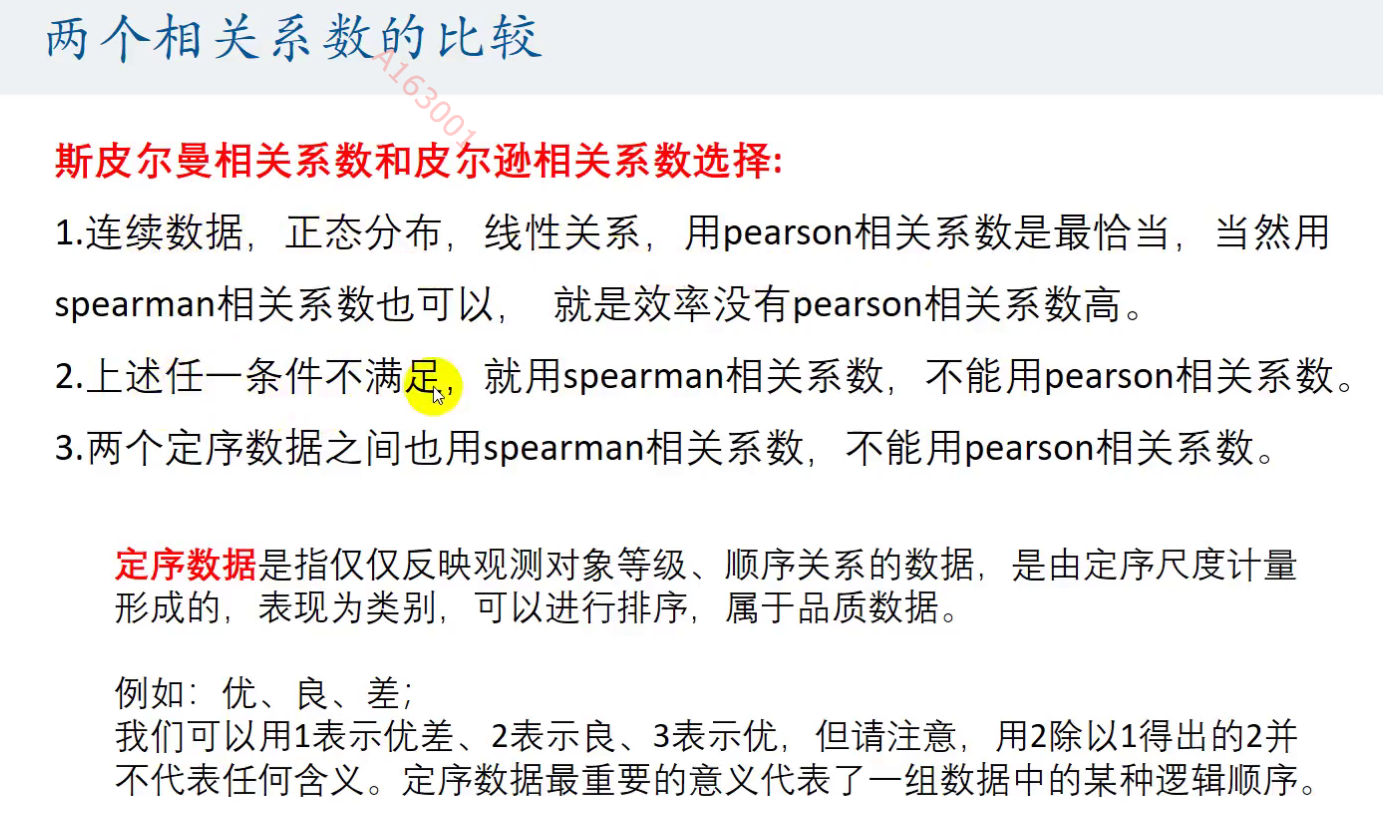
斯皮尔曼相关系数

　　由于皮尔曼相关系数的条件过多，时常满足不了，于是我们可以使用另一种相关系数

 　　　　

 　　　　

 　　　　 　

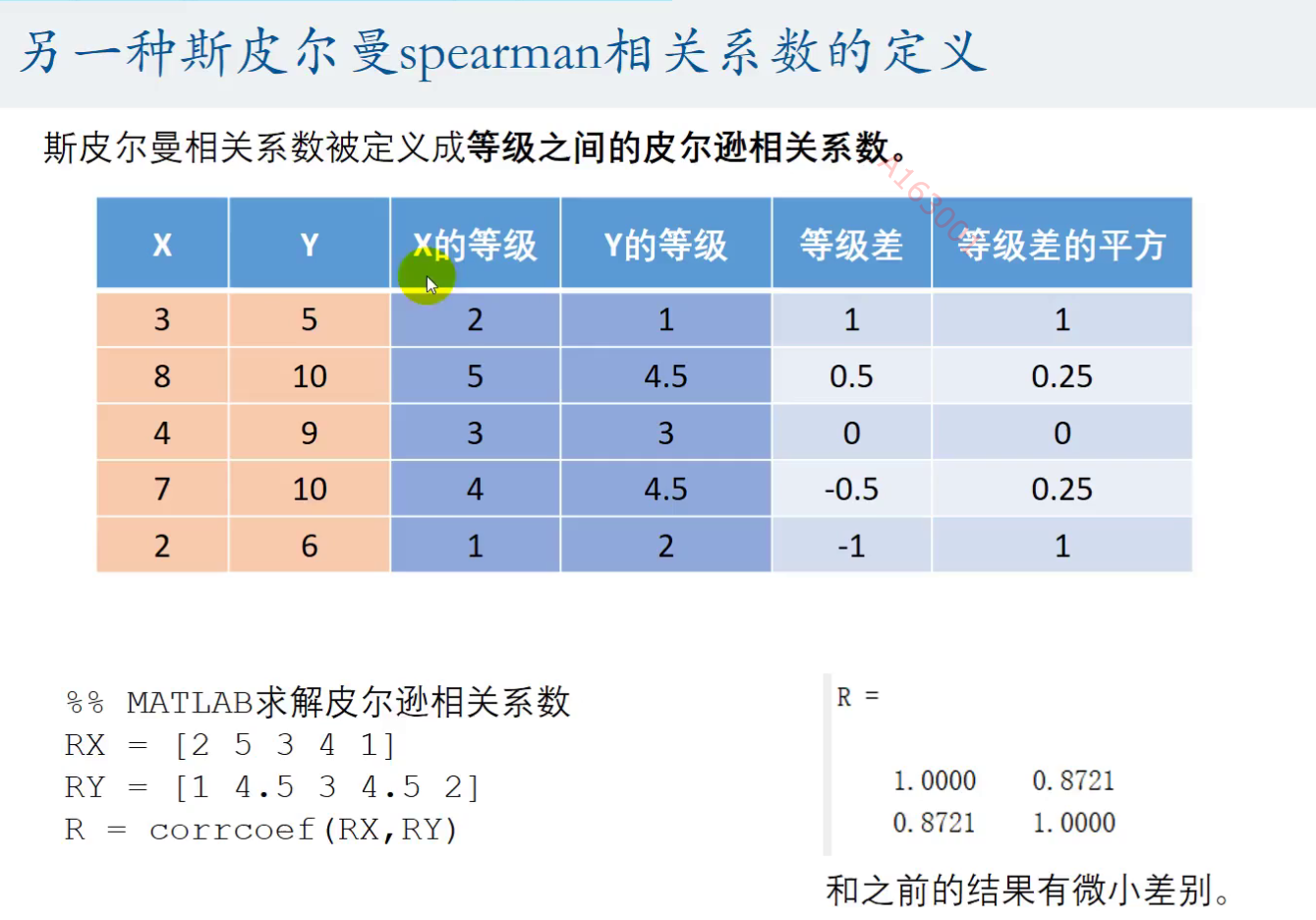
　　Matlab中使用函数计算斯皮尔曼相关系数

　　　　

 　　

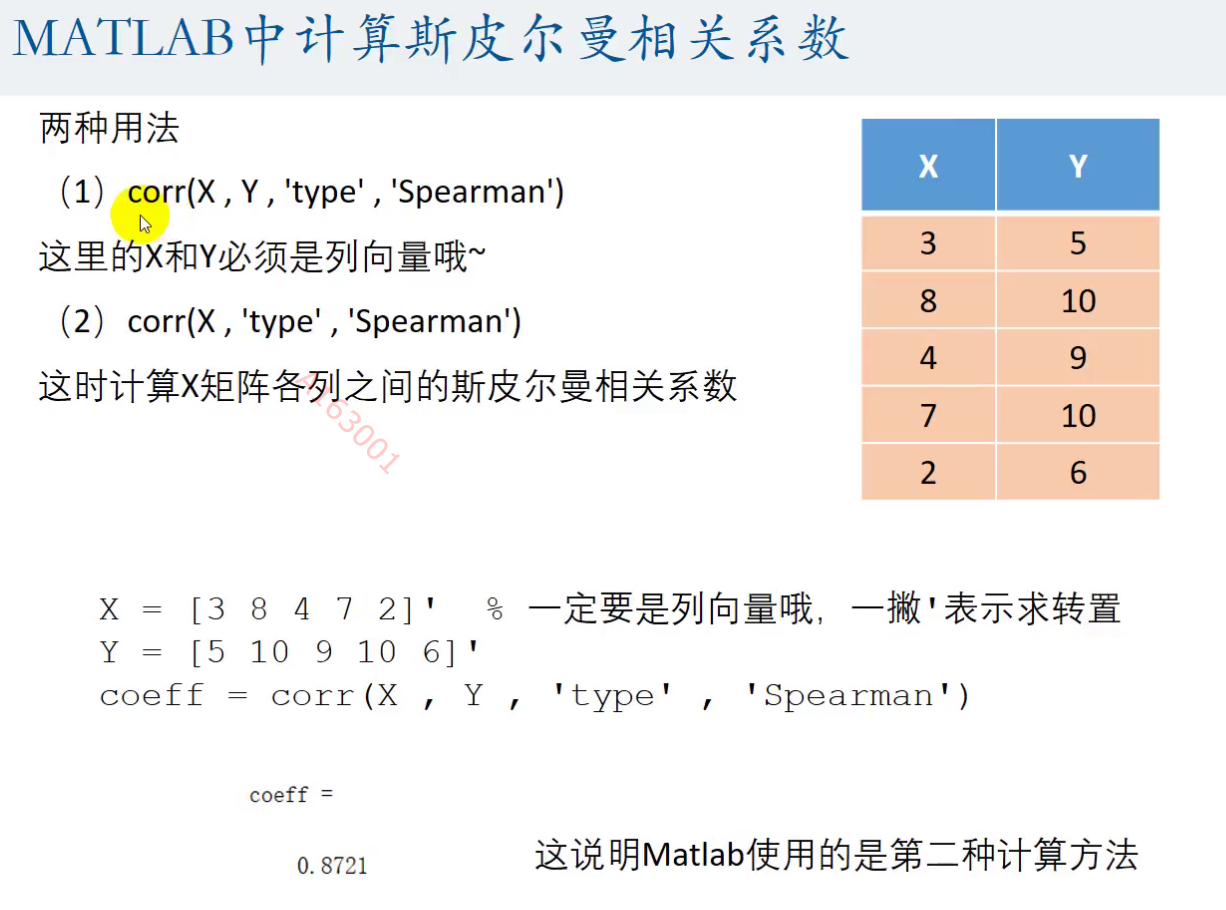
 　　　　这个X可以是我们上面提到的，这个数据矩阵

 　　　　

 　　　　得到的coeff就是我们需要的两两之间的相关系数矩阵

　　　　

　　　　对相关系数进行假设检验

　　　　

 　　　　

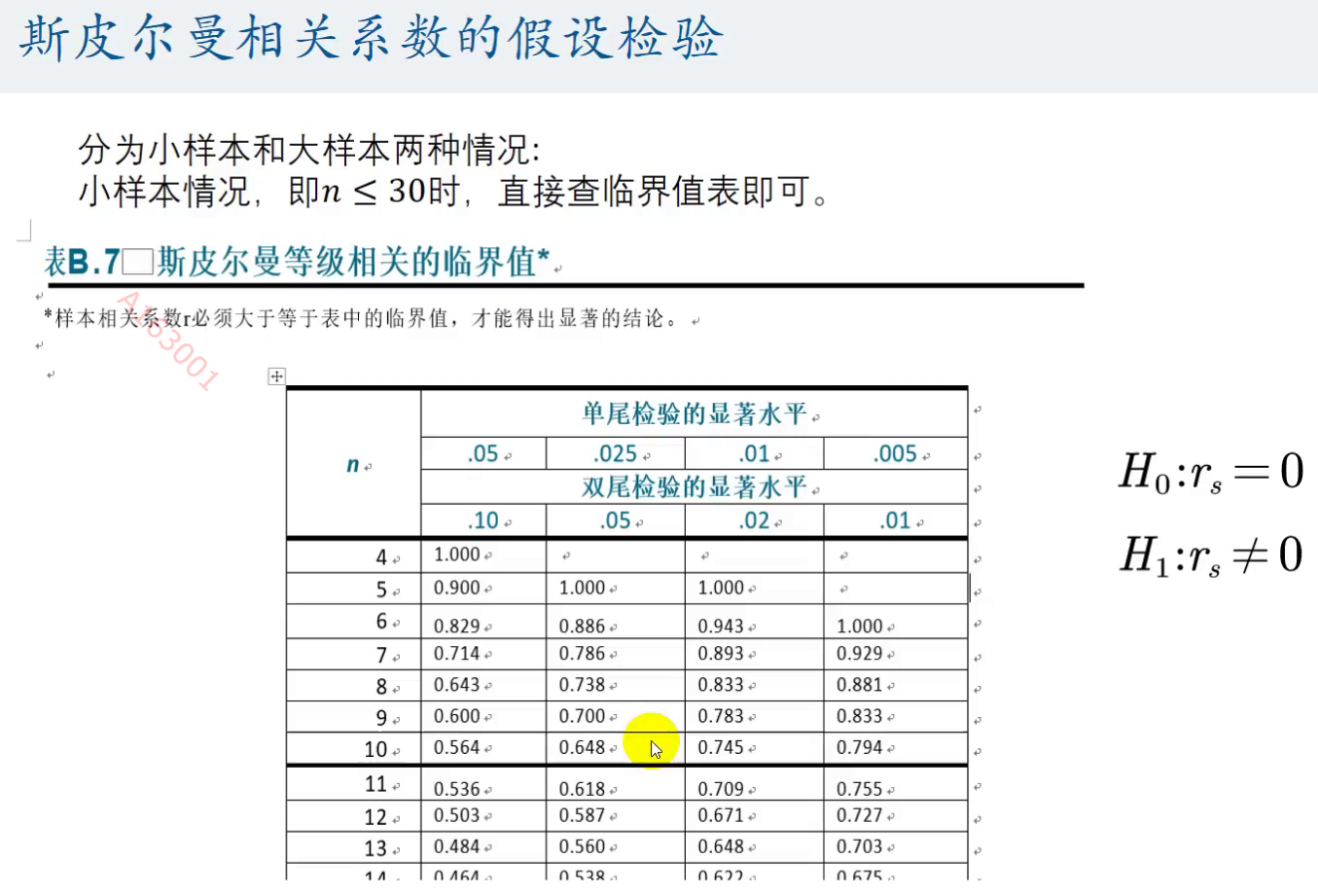
 　　　　　　小样本情况下，我们直接查表

　　　　    我们一般都是双边检验（即双尾检验）取显著水平位0.05，即置信区间为0.95
　　　　　

 　　　　　　

 　　　　　　　即r>=表中的临界值，我们才能得出显著异于0

　　　　　　

　　　　

 　　　　　　

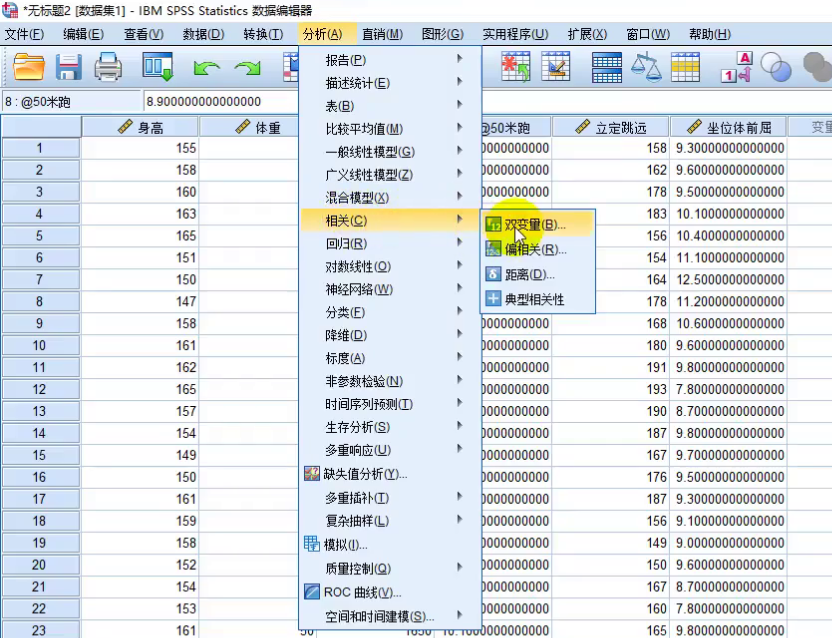
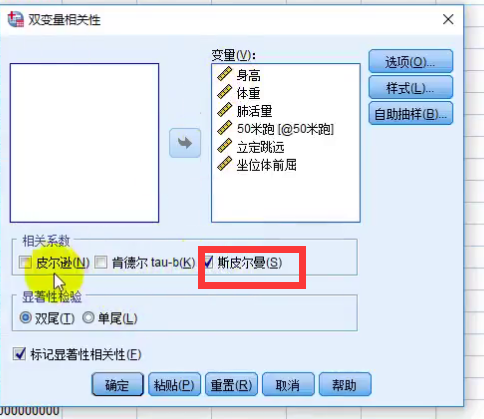
　　　　　　　　用SPSS快速计算：