蓝桥杯----图论训练
STL
当想要维护一个数组,其中的元素要求有序,同时可能随时对这个数组中的元素进行增减
有没有一个STL可以快速维护一个这样的数组?
multiset(平衡二叉树)




默认从小到大排序
注意离散化中清除重复元素的原理:
unique()函数

vector中的earse是删除指定一段,所以离散化有:

《树的直径》
什么是树的直径?
在一颗树上,两个叶子节点之间的最长距离下的路径

证明方式<------
如何dfs?
void dfs(int node,int fa)
{
if (maxL<deep[node])
d=node,maxL=deep[node];
for (int i=0;i<sides[node].size();i++)
{
int child=sides[node][i];
if (child==fa) continue;
deep[child]=deep[node]+1;
road[child]=node;
dfs(child,node);
}
}
d为我们要求的端点,每一次只要深度有更深的点我们就更新
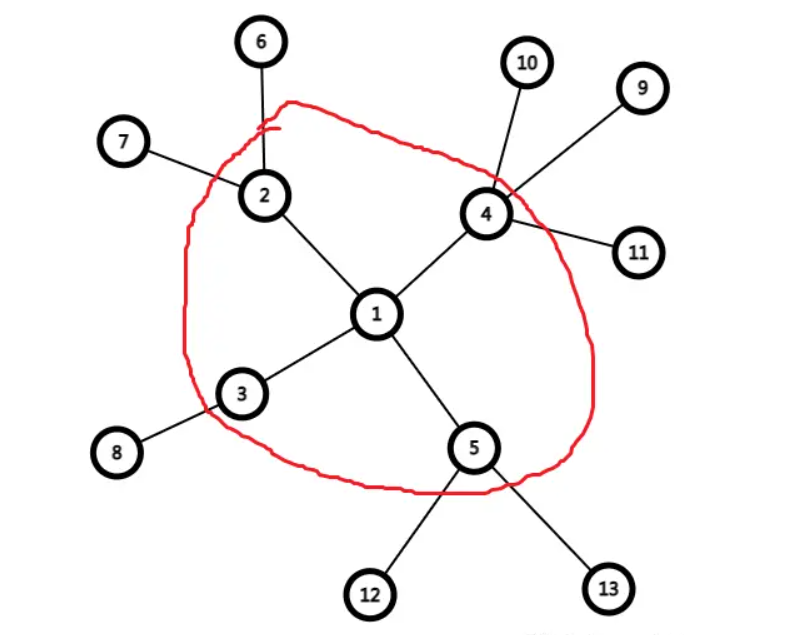
如何用拓扑排序的方式将叶子节点一圈一圈地给“减掉”?
双队列的方式,其中有个十分神奇的用法:
queue<int>q1,q2;
swap(q1,q2);
没想到swap可以直接交换队列
while (sum)
{
if (sum<=k)
break;
ans++;
while (q1.size())
{
int node=q1.front();
q1.pop();
sum--;
for (int i=0;i<sides[node].size();i++)
{
int next=sides[node][i];
if (du[next]<=1)
continue;
du[next]--;
if (du[next]==1)
q2.push(next);
}
}
swap(q1,q2);
}
《关于堆优化Dijkstra的st【】写法上的一点说明》
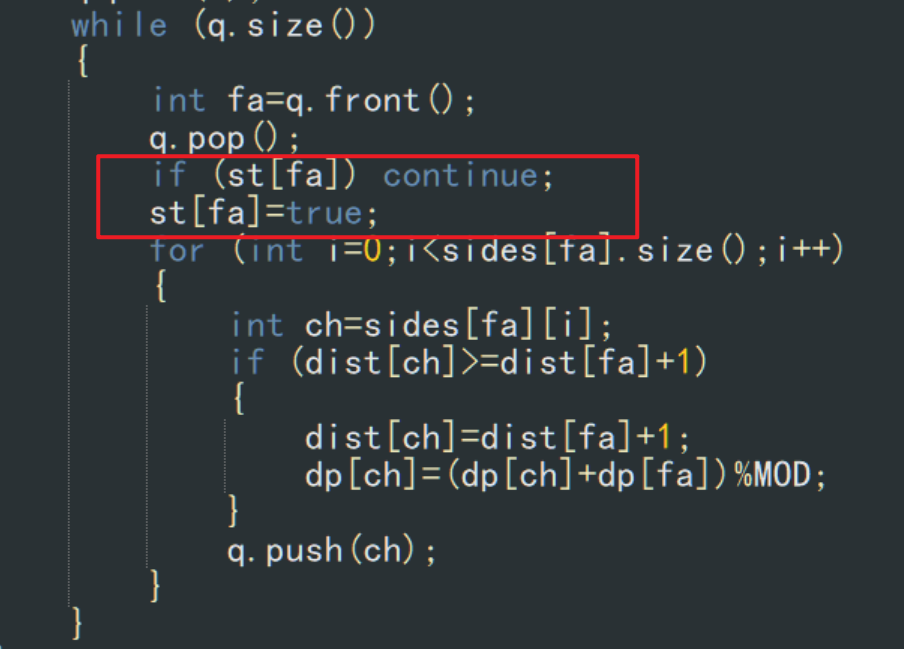
其实一般将这个st[]放到边的循环外面更好一点
主要是这样写简单,而且因为一般边的循环里面一般有判断
我们想要达到的目标是:
只是不让看过的点再次枚举他的边
而不是不能到这个点
还有写其他类似这中BFS的框架其实st【】放到哪里是不固定的
主要是看具体要求,有时这个st【】放到外面反而会错误
但是直接放外面简单
《最短路之分层最短路》
先通过一道题来看看什么是分层最短路:
题目链接<----


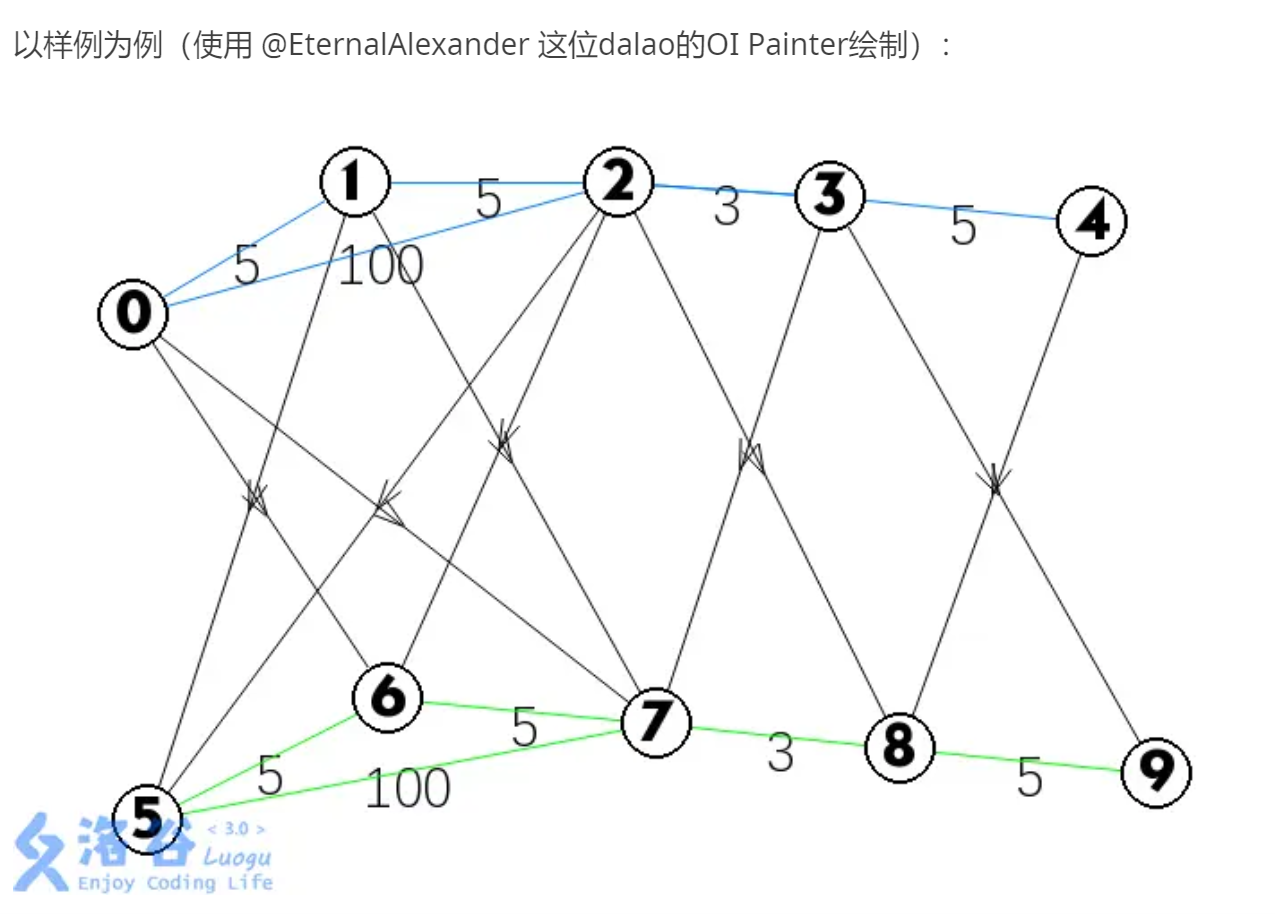
如果是题目输入建立出来的图就是如下:
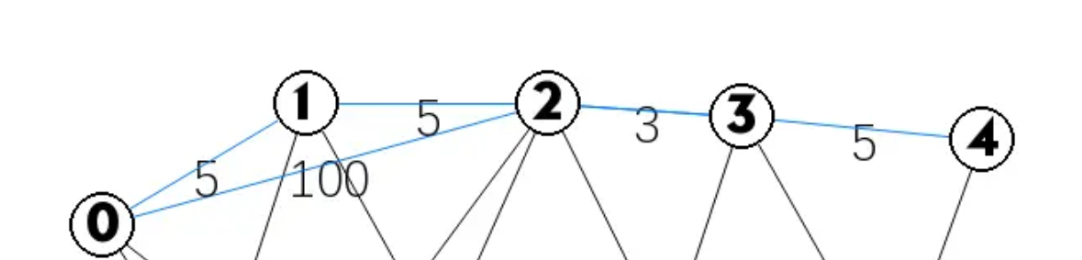
然后我们将决策的代价作为边的值,将到达的状态作为点
形成了层次图
可以看到其实每层中基本边的连接和点是与各层是一样的
这里的模板我比较推崇:
#include<cstdio>
#include<cctype>
#include<cstring>
#include<queue>
#include<algorithm>
#include<vector>
#include<utility>
#include<functional>
int Read()
{
int x=0;char c=getchar();
while(!isdigit(c))
{
c=getchar();
}
while(isdigit(c))
{
x=x*10+(c^48);
c=getchar();
}
return x;
}
using std::priority_queue;
using std::pair;
using std::vector;
using std::make_pair;
using std::greater;
struct Edge
{
int to,next,cost;
}edge[2500001];
int cnt,head[110005];
void add_edge(int u,int v,int c=0)
{
edge[++cnt]=(Edge){v,head[u],c};
head[u]=cnt;
}
int dis[110005];
bool vis[110005];
void Dijkstra(int s)
{
memset(dis,0x3f,sizeof(dis));
dis[s]=0;
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > points;
points.push(make_pair(0,s));
while(!points.empty())
{
int u=points.top().second;
points.pop();
if(!vis[u])
{
vis[u]=1;
for(int i=head[u];i;i=edge[i].next)
{
int to=edge[i].to;
if(dis[to]>dis[u]+edge[i].cost)
{
dis[to]=dis[u]+edge[i].cost;
points.push(make_pair(dis[to],to));
}
}
}
}
}
int main()
{
int n=Read(),m=Read(),k=Read(),s=Read(),t=Read();
int u,v,c;
for(int i=0;i<m;++i)
{
u=Read(),v=Read(),c=Read();
add_edge(u,v,c);
add_edge(v,u,c);
for(int j=1;j<=k;++j)
{
add_edge(u+(j-1)*n,v+j*n);
add_edge(v+(j-1)*n,u+j*n);
add_edge(u+j*n,v+j*n,c);
add_edge(v+j*n,u+j*n,c);
}
}
for(int i=1;i<=k;++i)
{
add_edge(t+(i-1)*n,t+i*n);
}//预防奇葩数据
Dijkstra(s);
printf("%d",dis[t+k*n]);
return 0;
}
这样的写法,首先就是按照层次图的样子将边建立好
然后直接跑Dijkstra,主要是因为这样简单好想
还一种写法是DP的写法,对于我来说如果条件复杂一点dp容易写错
这样的写法要注意的点是:
注意将全部的边都连好,不要漏边了,特别是在图是双向图的情况下

还是很有特征的:
进行决策,决策不影响图的结构,只影响当前的状态
层次图如下:一点都不层次
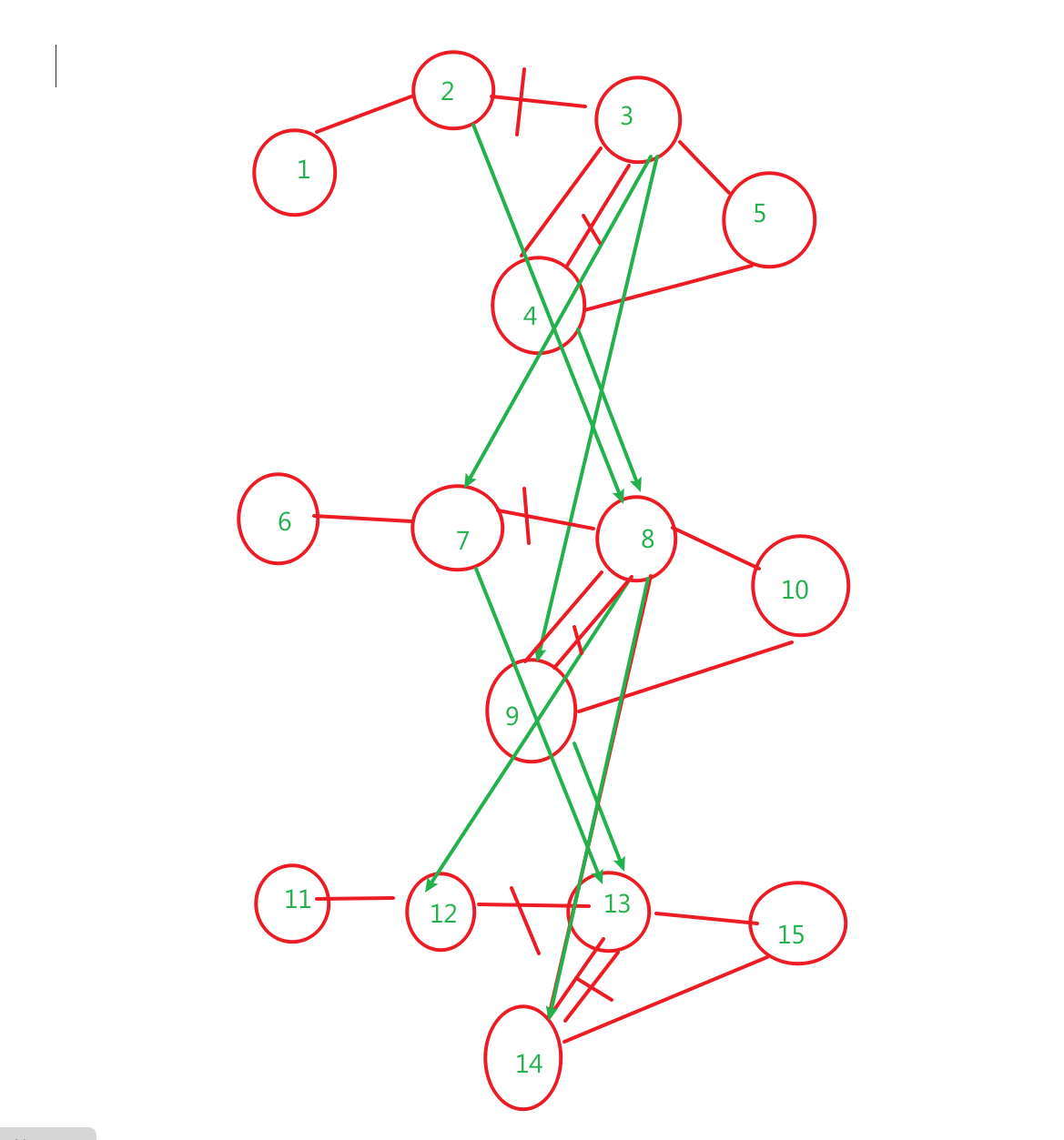
需要注意的是:
往下层走是单向的
下面这份代码是错误的,但是是给我做模板用的:
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
const int N=10005,K=10;
struct node{
int nd,dt;
bool operator<(const node &t)const
{
return dt>t.dt;
}
};
priority_queue<node>pq;
vector<node>sides[N*K];
int dist[N*K],n,m;
bool st[N*K];
void Dijkstra()
{
memset(dist,0x3f,sizeof(dist));
pq.push({1,0});
dist[1]=0;
while (pq.size())
{
int fnd=pq.top().nd,fdt=pq.top().dt;
pq.pop();
if (st[fnd])
continue;
st[fnd]=true;
for (int i=0;i<sides[fnd].size();i++)
{
int cnd=sides[fnd][i].nd,cw=sides[fnd][i].dt;
if (dist[cnd]>dist[fnd]+cw)
{
dist[cnd]=dist[fnd]+cw;
pq.push({cnd,dist[cnd]});
}
}
}
}
int main()
{
cin>>n>>m;
for (int i=1;i<=m;i++)
{
int a,b,c,d;
cin>>a>>b>>c>>d;
if (d)
sides[a].push_back({b+n,c}),
sides[a+n].push_back({b+2*n,c}),
sides[b].push_back({a+n,c}),
sides[b+n].push_back({a+2*n,c});
else
sides[a].push_back({b,c}),
sides[b].push_back({a,c});
sides[a+n].push_back({b+n,c}),
sides[b+n].push_back({a+n,c}),
sides[a+2*n].push_back({b+2*n,c}),
sides[b+2*n].push_back({a+2*n,c});
}
Dijkstra();
cout<<dist[n]-min(dist[3*n],min(dist[n],dist[2*n]));
return 0;
}
《将题目图论化》
题目链接<-----

其实对于一个题目只要有类似节点(状态)和边的模型出来
就可以将其看成图来想了
这道题我们可以将数当成点,按钮按一下到另一个点,明显这个
这个可以想象成边,权重是1,
是1的权重用bfs最简单了
#include<iostream> #include<cstring> #include<algorithm> #include<vector> #include<queue> using namespace std; const int N=1e5+5; int n,k; int arr[N],ans=0,dist[N]; vector<int>sides[N]; bool st[N]; void bfs(int root) { memset(dist,0x3f,sizeof(dist)); queue<int>q; q.push(root); dist[root]=0; while (q.size()) { int node=q.front(); q.pop(); if (st[node]) continue; st[node]=true; ans=max(ans,dist[node]); for (int i=0;i<sides[node].size();i++) { int child=sides[node][i]; dist[child]=min(dist[child],dist[node]+1); q.push(child); } } } int main() { cin>>n>>k; for (int i=0;i<n;i++) arr[i]=i; for (int i=0;i<n;i++) { int to=arr[(i+1)%n],tw=arr[(i+k)%n]; sides[i].push_back(to),sides[i].push_back(tw); } bfs(0); cout<<ans<<endl; return 0; }
环问题
当看到环的时候应该要想到两个基本的解决方法:
1.并查集
2.拓扑
来看一道题目:

首先从并查集的角度来想吧:
想想并查集在kruskal算法的运用

我们在合并的时候是不是要用find()函数判断两个点的父节点是否是同一个?
如果是同一个,我们如果再合并这两个点(即将这两个点用边连起来)
是不是会形成环?
根据这个思想,我们可以不断地选择边,然后尝试将边上两个端点合并(即连接这两个端点)
直到遇到了两个端点(假设这两个端点为a,b)的父节点是一样,说明再合并就要成环了
我们不再合并,这个时候的图是颗树,我们知道会造成环的端点是a,b
因为在树上从一个端点到另一个端点的路径是唯一的
我们就可以从a dfs 到 b ,期间记录一下在这条路径上看过哪些点
这些点就是环上的点
#include<iostream> #include<cstring> #include<algorithm> #include<vector> using namespace std; const int N=1e5+5; int n,from[N],to[N],h[N]; vector<int>sides[N]; int find(int x) { if (h[x]!=x) h[x]=find(h[x]); return h[x]; } bool st[N]; void dfs(int sta,int fin) { if (sta==fin) { for (int i=1;i<=n;i++) if (st[i]) cout<<i<<" "; return ; } for (int i=0;i<sides[sta].size();i++) { int child=sides[sta][i]; if (st[child]) continue; st[child]=true; dfs(child,fin); st[child]=false; } } int main() { cin>>n; for (int i=1;i<=n;i++) { cin>>from[i]>>to[i]; h[i]=i; } for (int i=1;i<=n;i++) { int a=from[i],b=to[i]; int fa=find(a),fb=find(b); if (fa!=fb) { h[fb]=fa; sides[a].push_back(b),sides[b].push_back(a); } else { st[a]=true; dfs(a,b); break; } } return 0; }
在来从拓扑的角度来想:
我们不断地将没有环的节点拿掉,哪些那不掉的节点不就是环上的节点吗?
注意topsort的写法:
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
const int N=1e5+5;
int n,rd[N];
vector<int>sides[N];
bool st[N];
void topsort()
{
queue<int>q;
for (int i=1;i<=n;i++)
if (rd[i]<=1)
{
q.push(i);
st[i]=true;
}
while (q.size())
{
int fa=q.front();
q.pop();
for (int i=0;i<sides[fa].size();i++)
{
int child=sides[fa][i];
if (st[child])
continue;
rd[child]--;
if (rd[child]<=1)
{
st[child]=true;
q.push(child);
}
}
}
}
vector<int>ans;
int main()
{
cin>>n;
for (int i=1;i<=n;i++)
{
int a,b;
cin>>a>>b;
rd[a]++,rd[b]++;
sides[a].push_back(b),sides[b].push_back(a);
}
//注意在topsort之前需要将全部的已经是叶子节点的点全部
//记录下来,否则会出错,而不是像下面这样只记录一个点
/*int sta;
for (int i=1;i<=n;i++)
if (rd[i]<=1)
{
sta=i;
break;
}*/
topsort();
for (int i=1;i<=n;i++)
if (!st[i])
ans.push_back(i);
sort(ans.begin(),ans.end());
for (int i=0;i<ans.size();i++)
cout<<ans[i]<<" ";
return 0;
}
模板错误记录
《LCA》
#include<iostream> #include<cstring> #include<algorithm> #include<vector> #include<queue> using namespace std; const int N=1e5+5; int n,m,root=1; vector<int>sides[N]; int lazy[N]; //需要注意的点:f[N][20]这样开是错误的, //我循环了20次,而这样数组下标就溢出了,会产生十分奇怪的错误 int deep[N],dist[N],f[N][25]; void bfs() { //这里deep一定要初始化为0x3f3f3f3f,因为下面LCA中防止跳出界限要用到 //同时主要要将0的deep初始化为0, memset(deep,0x3f,sizeof(deep)); queue<int>q; q.push(root); deep[0]=0,deep[root]=1,dist[root]=lazy[root]; while (q.size()) { int fa=q.front(); q.pop(); for (int i=0;i<sides[fa].size();i++) { int child=sides[fa][i]; if (deep[child]<deep[fa]) continue; deep[child]=deep[fa]+1; dist[child]=dist[fa]+lazy[child]; f[child][0]=fa; for (int j=1;j<=20;j++) //注意这里是j-1,而不是j/2 f[child][j]=f[f[child][j-1]][j-1]; q.push(child); } } } int LCA(int a,int b) { //a永远是深度更深的那个点 if (deep[a]<deep[b]) swap(a,b); //首先要将点a跳到与b点相同的深度 for (int i=20;i>=0;i--) { if (deep[f[a][i]]>=deep[b]) a=f[a][i]; } if (a==b) return a; //a与b一起跳 for (int i=20;i>=0;i--) { if (f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i]; } return f[a][0]; } int main() { cin>>n>>m; for (int i=1;i<=n-1;i++) { int a,b; cin>>a>>b; sides[a].push_back(b),sides[b].push_back(a); lazy[a]++,lazy[b]++; } bfs(); while (m--) { int a,b; cin>>a>>b; int lca=LCA(a,b); cout<<dist[a]+dist[b]-2*dist[lca]+lazy[lca]<<endl; } return 0; }
<Floyd>
#include<iostream> #include<cstring> #include<algorithm> using namespace std; const int N=205,INF=0x3f3f3f3f; int n,m,Time[N]; int dp[N][N][N]; void floyd() { for (int k=1;k<=n;k++) for (int i=1;i<=n;i++) for (int j=1;j<=n;j++) //注意这里是 dp[k-1][i][j] 而不是dp[k][i][j] dp[k][i][j]=min(dp[k-1][i][j], dp[k-1][i][k]+dp[k-1][k][j]); } int main() { cin>>n>>m; memset(dp,0x3f,sizeof(dp)); //注意如果这里最求模拟的真实性的话需要将自己到自己 //初始化为0 for (int i=0;i<=n;i++) for (int j=1;j<=n;j++) dp[i][j][j]=0; for (int i=1;i<=n;i++) cin>>Time[i]; for (int i=1;i<=m;i++) { int a,b,w; cin>>a>>b>>w; a++,b++; dp[0][a][b]=dp[0][b][a]=w; } floyd(); int q; cin>>q; while (q--) { int a,b,t; cin>>a>>b>>t; a++,b++; if (Time[a]>t || Time[b]>t) { cout<<-1<<endl; continue; } int maxn; for (int i=1;i<=n;i++) { if (Time[i]<=t) maxn=i; else break; } if (dp[maxn][a][b]<INF) cout<<dp[maxn][a][b]<<endl; else cout<<-1<<endl; } return 0; }
《topsort》
//注意在topsort之前需要将全部的已经是叶子节点的点全部
//记录下来,否则会出错,而不是像下面这样只记录一个点
/*int sta;
for (int i=1;i<=n;i++)
if (rd[i]<=1)
{
sta=i;
break;
}*/
topsort();


 浙公网安备 33010602011771号
浙公网安备 33010602011771号