2023_4_5 蓝桥杯练习

《P8671 [蓝桥杯 2018 国 AC] 约瑟夫环  循环（%）问题》

 

 

 　　我尝试用STL中的list 与 vector 进行模拟

　 可以发现复杂度都是>=O(N*K)的，会超时

　　只有通过数学推式来得到全部正确的答案

　

　这里简单说一下STL list 与 vector中对插入，删除元素的用法：

　　list:

　　　　

 

 

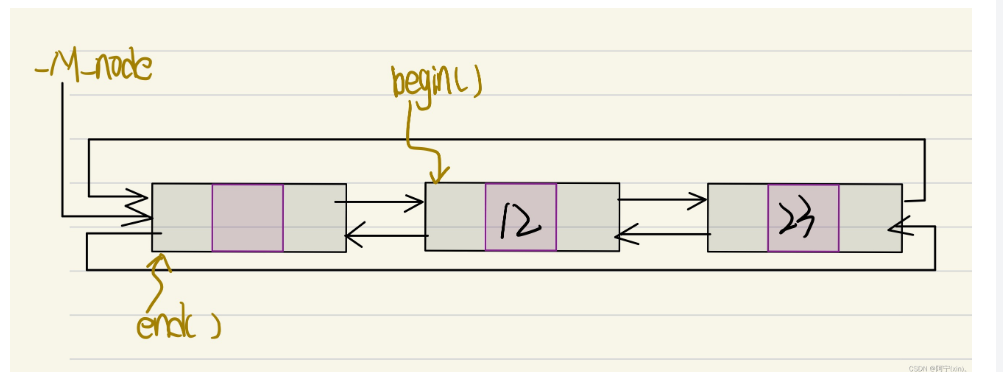
 　　　　　　　当使用list的时候用迭代器 list<xxx>::iterator it 来访问其中的元素

　　　　注意对it进行初始化

　　　　list.push_back()

　　　　list.push_front()

　　　　list.erase(it)

　　　　注意当删除后，it依然指向的是删除的节点，所以我们要像使用c的原始指针一样使用list

　　　　最好用 preit,it双指针来实现

　　　　注意迭代器只能通过 ++ 来移动，而不能通过+=来移动

　　　

　　vector

　　　　vector<xxx>a

　　　　可以通过如 

　　　　　　rm是目标节点相对于开始节点处的距离

　　　　　　a.erase(a.begin()+rm)

　　　　　　来实现删除，但是删除的复杂度有点高

　　　　　　想比于上面的双指针，这个操作更加不容易出错

　　

　　接下来说说真正的解法：

　　　　首先对于 循环（%）的问题

　　　　将位置下标设置为从0开始更好，可以避免特殊处理：

　　　　　　如1~10， %10

　　　　　　当到下标10的时候还要处理下0的问题

　　　　　如果设置成0~9 ,%10 就完全不用担心这个问题了

　　

　　同时在写 循环 （%）的问题，在打草稿的时候

　　　　不要一个劲地在一行上思考

　　　　而是如：

　　　　　　

 

 

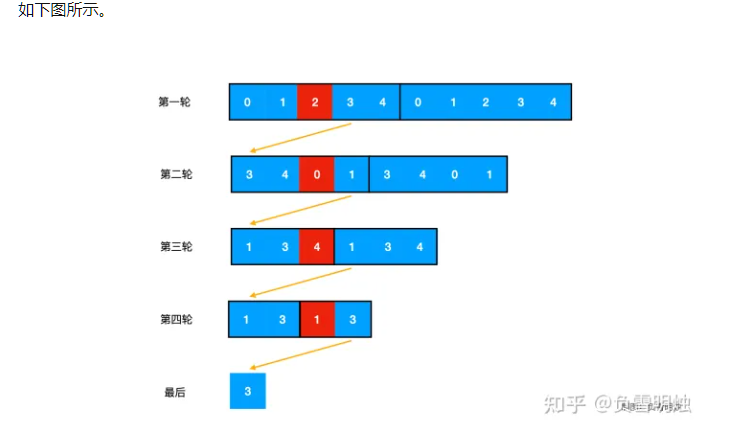
 　　　　　　　　　　这样会更能发现规律

　　　　大佬博客 <-----

　　　

 

 

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int main()
{
    int n, m;
    cin >> n >> m;
    int pos = 0;
    for (int i = 2; i <= n; i++)
        pos = (pos + m) % i;
    cout << pos + 1;
    return 0;
}

 

 　　　　　　

 《P8755 [蓝桥杯 2021 省 AB2] 负载均衡  模拟问题》

 

 

 　　　　

　　　　当时是不用时刻监视着每一个时间段上是否有任务好了没有

　　 而是当题目给出了一个时间，看小于这个时间上的时间段上是否有任务好了

　　 那么如何去做到这一点？

　　　　于是我开始了傻呼呼，而且容易错的暴力模拟

　　其实用堆，排序关键字是完成的时间就可以了

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <map>
#include <vector>
#include <queue>
using namespace std;
const int N = 2 * 1e5 + 2;
typedef long long ll;
ll vs[N];
int n, m;
struct node
{
    ll t, nt, id, cost;
    bool operator<(const node &y) const
    {
        return t + nt > y.t + y.nt;
    }
};
priority_queue<node> pq;
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> vs[i];
    for (int i = 1; i <= m; i++)
    {
        ll t, id, nt, cost;
        cin >> t >> id >> nt >> cost;

        // 我这里逻辑错误了,是只有当成功了才进行这次分配
        // 而不是一开始就进行分配
        /* pq.push({t, nt, id, cost}); */

        while (pq.size() && (pq.top().t + pq.top().nt <= t))
        {
            vs[pq.top().id] += pq.top().cost;
            pq.pop();
        }
        if (vs[id] >= cost)
        {
            pq.push({t, nt, id, cost});
            vs[id] -= cost;
            cout << vs[id] << endl;
        }
        else
            cout << -1 << endl;
    }
    return 0;
}

 

 

 

《P8756 [蓝桥杯 2021 省 AB2] 国际象棋》

 

 

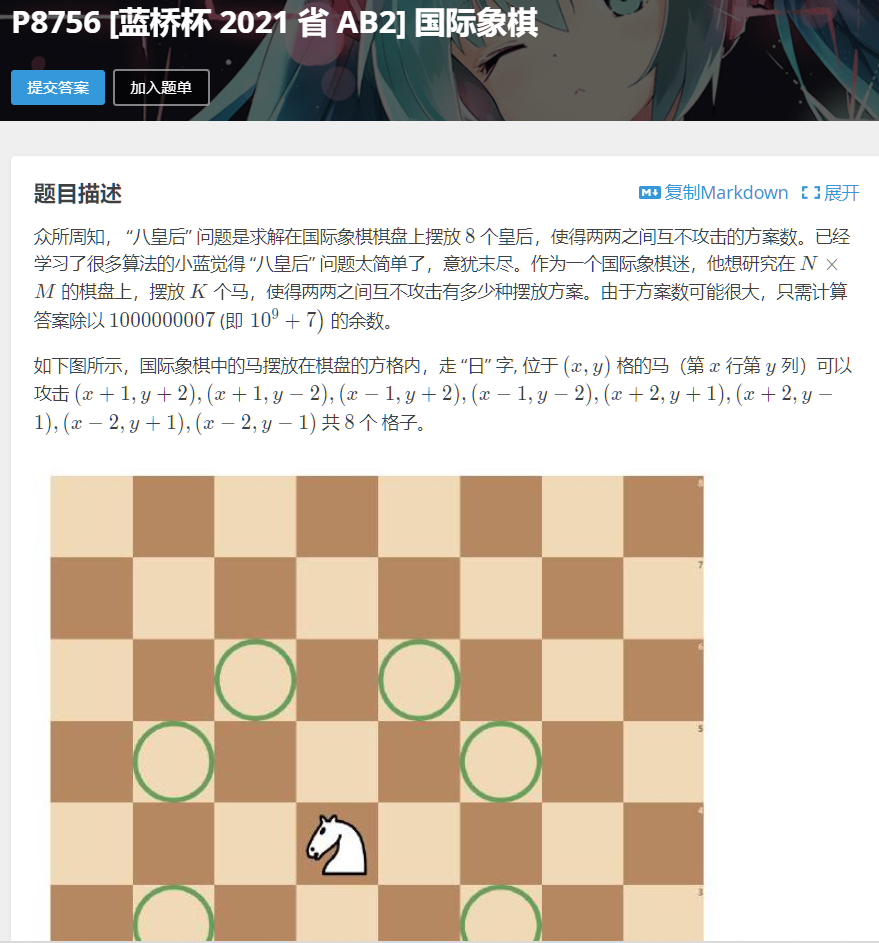
 　　这道题主要麻烦的是

　 判断马在每行排放的状态是否可以（以状态压缩dp的思想）

　 比如 s1,s2,s3分别是这一行，上一行，上上行的状态

　 那么如何判断是否可行？

　 其实我们发现

　　对于s1在二进制下，如果某位上是1 ，

　　　　那么对于s2,这一位的左两位与右两位上一定不能是1

　　　　即 s2 & (s1>>2) || s2 & (s1<<2) 为真 就不行

　　　　对于s3 ,这一位的左1位于右一位上一定不能是1

　　　　即 s3 & (s1>>1) || s3 & (s1<<1) 为真 就不行