AtCoder Beginner Contest 291

《D - Flip Cards Editorial》

　　

 

 

　　 　　简单dp,只是我当时在写的时候忘记%mod了

　　  人麻了

#include <iostream>
#include <algorithm>
#include <cstring>
#include <map>
using namespace std;
const int N = 2 * 1e5 + 2, mod = 998244353;
int cards[N][2];
long long dp[N][2];
int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> cards[i][0] >> cards[i][1];
    dp[1][0] = 1, dp[1][1] = 1;
    for (int i = 2; i <= n; i++)
        for (int j = 0; j <= 1; j++)
        {
            if (cards[i][j] != cards[i - 1][0])
                dp[i][j] = (dp[i][j] + dp[i - 1][0]) % mod;
            if (cards[i][j] != cards[i - 1][1])
                dp[i][j] = (dp[i][j] + dp[i - 1][1]) % mod;
        }
    cout << (dp[n][0] + dp[n][1]) % mod << endl;
    return 0;
}

　　

《E - Find Permutation Editorial》

　　

 

 

 　　　　这道题很明显是一个偏序

　　  其可以对应着一个拓扑图

　　　问A是否是唯一的，即问拓扑图的拓扑序是否唯一

　　　判断拓扑序是否唯一即看每一次下一次要选择的点是否是唯一的

　　   即每一次入度为0的点是否超过1个

　

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
#include <map>
using namespace std;
const int N = 2 * 1e5 + 2;
int n, m;
int cd[N], rd[N], a[N];
queue<int> q, ans;
bool solve(int sta, vector<vector<int>> sides)
{
    q.push(sta);
    int cZ = 1;
    while (q.size())
    {
        int t = q.front();
        /*   cout << "t: " << t << endl; */
        ans.push(t);
        q.pop();
        cZ--;
        for (int to : sides[t])
        {
            /* cout << "to: " << to << endl; */
            rd[to]--;
            if (rd[to] == 0)
            {
                cZ++;
                /*  cout << "cZ: " << cZ << endl; */
                if (cZ > 1)
                    return false;
                q.push(to);
            }
        }
    }
    if (ans.size() < n)
        return false;
    return true;
}
int main()
{
    cin >> n >> m;
    vector<vector<int>> sides(n + 1);
    for (int i = 1; i <= m; i++)
    {
        int a, b;
        cin >> a >> b;
        sides[a].push_back(b);
        cd[a]++, rd[b]++;
    }
    int sta = -1;
    for (int i = 1; i <= n; i++)
        if (rd[i] == 0)
            sta = i;
    /* cout << sta << endl; */
    if (sta == -1)
    {
        cout << "No" << endl;
        return 0;
    }
    if (!solve(sta, sides))
        cout << "No" << endl;
    else
    {
        cout << "Yes" << endl;
        int cnt = 1;
        while (ans.size())
        {
            int t = ans.front();
            ans.pop();
            a[t] = cnt;
            cnt++;
        }
        for (int i = 1; i <= n; i++)
            cout << a[i] << " ";
        cout << endl;
    }
    return 0;
}

 

　《F - Teleporter and Closed off Editorial》

 

 　　　　这道题其实看条件

 

 

 　　　　我就觉得有点floyd算法dp含义的内味了

　　　再看N很大，M却很小

　　　

 

 

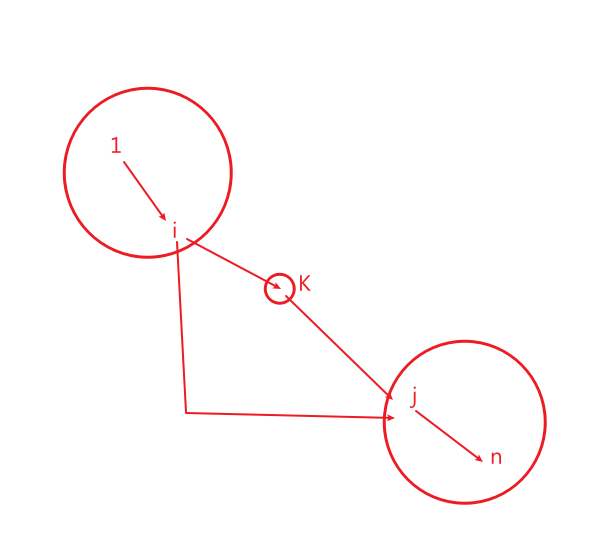
 　　　　　　1->n的最短路可以通过dp[1][k]+dp[k][n]得到（dp[i][j]:表示点i到点j的最小距离）

　　　   现在不允许用点k，那么必须用其他点来连接1与n

　　　　现在有个暴力的想法：

　　　　　　枚举i和j ,求出dp[1][i]+dp[j][n]的最小值

　　　　但是如何确定这个过程中没有点k的参与呢？

　　　　而且这样作时间复杂度也不允许

　　　　同时i与j可能也没有边相连

　　　　　　对，没有边相连这个是关键

　　　　　　想一下这个题目中有边相连的条件是啥？

　　　　　　1<=j-i<=m

　　　　　　m是不是很小？

　　　　　　所以我们没必要枚举全部的i和j

　　　　　　同时也要保证dp[1][i]和dp[j][n]一定不是通过k点得来的

　　　　　　那么就是枚举在k点旁边的点i,j，保证i<k,j>k

　　　　　　同时1<=j-i<=m

　

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 2, INF = 0x3f3f3f3f;
// dp0[i]：表示从点1到点i的最小距离
// dp1[i]:表示从点i到点n的最小距离
int dp0[N], dp1[N], n, m;
int ans[N];
string strs[N];
void get(int a[], int len)
{
    for (int i = 1; i <= len; i++)
        cout << a[i] << " ";
    cout << endl;
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> strs[i];
    memset(dp0, 0x3f, sizeof(dp0));
    memset(dp1, 0x3f, sizeof(dp1));
    dp0[1] = 0;
    for (int i = 1; i <= n; i++)
        for (int j = max(1, i - m); j <= i - 1; j++)
            if (strs[j][i - j - 1] == '1')
                dp0[i] = min(dp0[i], dp0[j] + 1);
    /* get(dp0, n); */
    dp1[n] = 0;
    for (int i = n; i >= 1; i--)
        for (int j = i + 1; j <= min(n, i + m); j++)
            if (strs[i][j - i - 1] == '1')
                dp1[i] = min(dp1[i], dp1[j] + 1);
    /*  get(dp1, n); */
    memset(ans, 0x3f, sizeof(ans));
    for (int k = 2; k <= n - 1; k++)
        for (int i = max(1, k - m); i <= k - 1; i++)
            for (int j = k + 1; j <= min(n, k + m); j++)
                if (j - i <= m && strs[i][j - i - 1] == '1')
                    ans[k] = min(ans[k], dp0[i] + dp1[j] + 1);
    for (int k = 2; k <= n - 1; k++)
    {
        if (ans[k] >= INF)
            cout << -1 << " ";
        else
            cout << ans[k] << " ";
    }
    cout << endl;
    return 0;
}