(AtCoder Beginner Contest 289)And Codeforces Round #851 (Div. 2)
<C - Coverage Editorial>


这道题可以用dfs进行爆搜,但是在爆搜的时候要注意:
是否同一个状态重复计数了
比如 dfs(int x,int state) 表示看第x个set的时候,是否选择Cx,目前state(是用二进制表示的是否含有第i个数的值)
可能在这个时候我就已经满足条件了ans++,目前是否选择Ci的状态是00001111(第i位代表着是否选择了Ci)
但是还不能返回,这个时候还要继续搜下去,搜到最后可能状态还是00001111,重复了
要避免在这个情况下ans还++
用dp可以不用去考虑这种情况
dp[i][state]:表示 在前i个set中选择,导致是否含有第i个数的状态为state的方案数
状态转移:
dp[i][state]+=dp[i-1][state]
dp[i][state“+”states[i]]+=dp[i-1][state]
(“+”表示特殊操作,具体看代码)
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
int dp[12][10000];
int states[12];
int get(int j, int state)
{
int ans = 0;
for (int i = 1; i <= n; i++)
{
int b1 = (j >> (i - 1)) & 1, b2 = (state >> (i - 1)) & 1;
int b = b1 | b2;
if (b)
ans += (1 << (i - 1));
}
return ans;
}
int main()
{
cin >> n >> m;
int need = ((1 << n) - 1);
for (int i = 1; i <= m; i++)
{
int g;
cin >> g;
for (int j = 1; j <= g; j++)
{
int num;
cin >> num;
states[i] += (1 << (num - 1));
}
}
dp[0][0] = 1;
for (int i = 1; i <= m; i++)
for (int j = 0; j <= need; j++)
{
dp[i][j] += dp[i - 1][j];
dp[i][get(j, states[i])] += dp[i - 1][j];
}
cout << dp[m][need];
return 0;
}
《D - Step Up Robot》

dp[x]:表示是否能到第x阶梯
状态转移:
dp[x]|=dp[x-steps[i]] (steps[i]是枚举的一次能够上多少个阶梯)
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int n, as[12], m, x;
bool traps[100001];
int dp[100001];
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
cin >> as[i];
cin >> m;
for (int i = 1; i <= m; i++)
{
int t;
cin >> t;
traps[t] = true;
}
cin >> x;
dp[0] = 1;
for (int i = 1; i <= x; i++)
{
for (int j = 1; j <= n; j++)
{
if (i >= as[j] && !traps[i - as[j]])
dp[i] |= dp[i - as[j]];
}
}
if (dp[x])
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}
《E - Swap Places 》
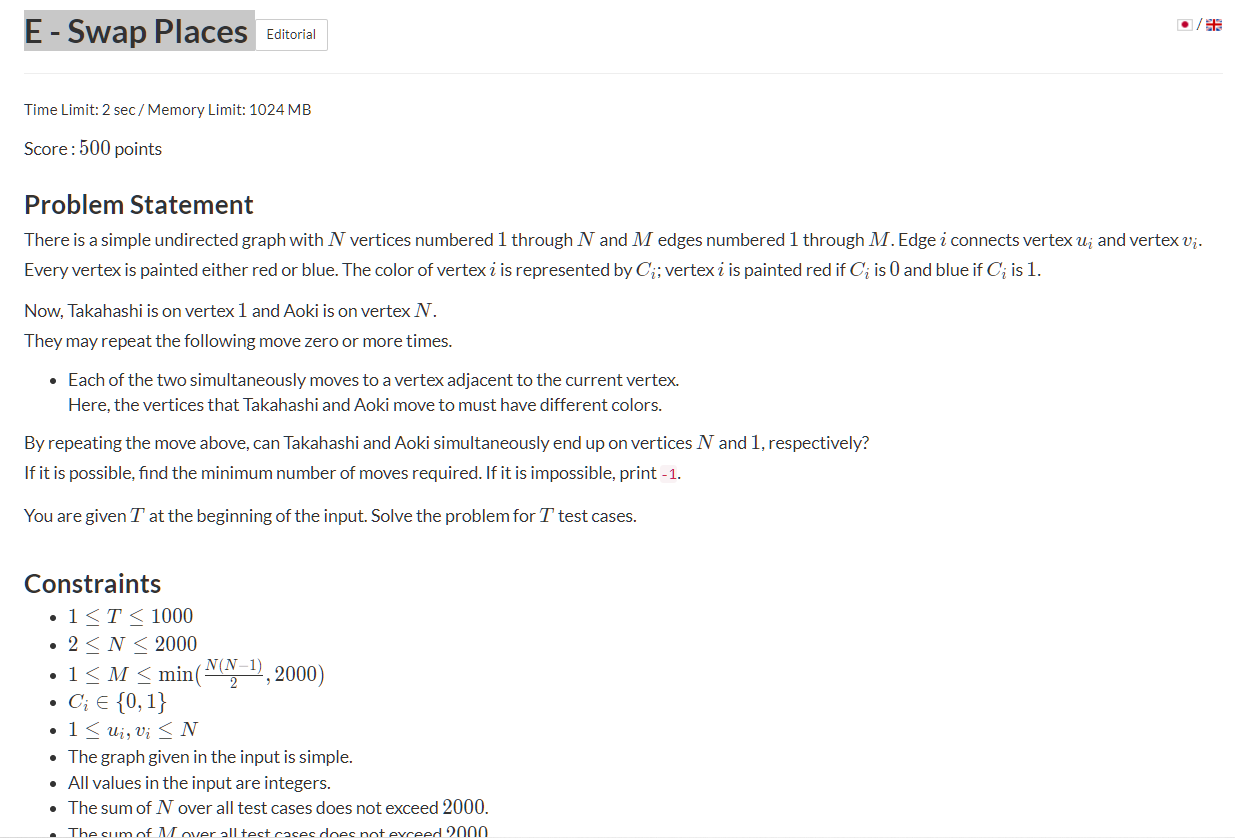
有点类似dp的思想,dp[T][A]:表示从初始的状态到Takahashi在点T,Aoki在点A时的这个状态的最小步数
然后状态的转移通过bfs来实现
其实如果先不考虑两个人走,一个人在一个图上,从一个点到另一个点的最小距离(在边权重都为1的情况下)
其实就是可以用BFS来做
现在这里两个人走,只是加了一点限制条件,方法还是一样的
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int INF = 0x3f3f3f3f;
int color[2001], t, n, m;
int bfs(int sta, int fin, vector<vector<int>> sides)
{
vector<vector<int>> dp(n + 1, vector<int>(n + 1, INF));
queue<PII> s;
s.push({sta, fin});
dp[sta][fin] = 0;
while (s.size())
{
auto t = s.front();
s.pop();
for (int a : sides[t.first])
for (int b : sides[t.second])
{
if (color[a] != color[b] && dp[a][b] > dp[t.first][t.second] + 1)
{
s.push({a, b});
dp[a][b] = dp[t.first][t.second] + 1;
}
}
}
return dp[n][1];
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> t;
while (t--)
{
cin >> n >> m;
vector<vector<int>> sides(n + 1);
for (int i = 1; i <= n; i++)
cin >> color[i];
for (int i = 1; i <= m; i++)
{
int a, b;
cin >> a >> b;
sides[a].push_back(b), sides[b].push_back(a);
}
int ans = bfs(1, n, sides);
if (ans >= INF)
cout << -1 << endl;
else
cout << ans << endl;
}
return 0;
}
《F - Teleporter Takahashi Editorial》
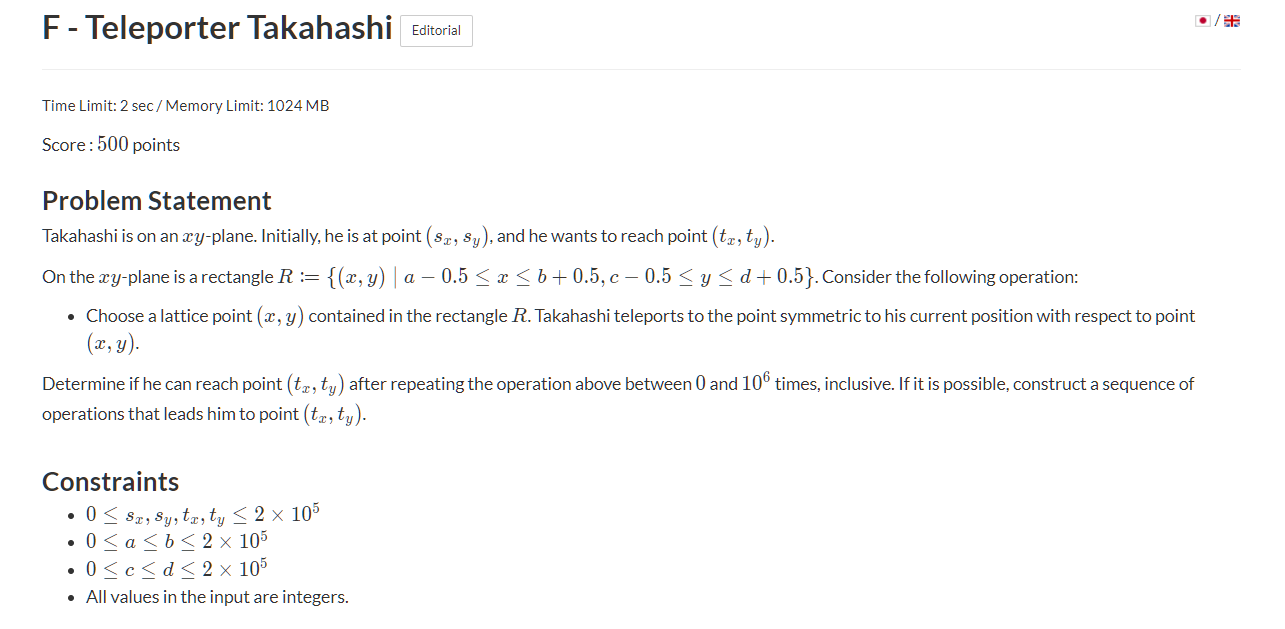
这道题目前我还是具体代码写不出(一些细节边界问题搞不出)
但是给了我一点写二维题目的启发:
将二维问题转化为一维问题来解决
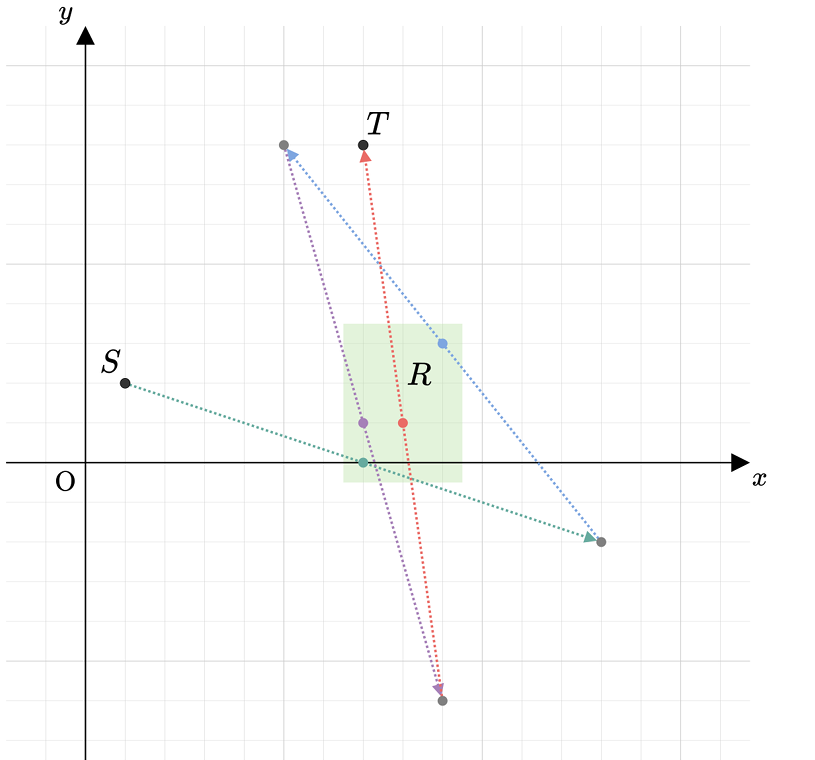
首先面对这道题,不能只考想象,要实际去动手画一下
想要将sx到tx,会发现
如 (sx,sy)关于(a,c)对称得到点(x,y)
(x,y)在关于(a+1,c)对称得到点(sx+2,y)
发现保持对称中心点的y不变,可以达到只改变x,而y不变的方法
不断通过上述操作,可以判断出是否可以sx->tx
y同理
同时还可以结合数学公式去理解
《B. Sum of Two Numbers》

这些思维题真是一看题解就会,感觉在写的时候再点一下就能写出来了,ORZ
开始这这里我做的时候只是简单的用n/2,没考虑到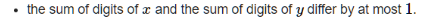
其实正确解法也就是/2
只是对于n(在十进制下)的每一位/2,将得到的数num,分配到x,y的对应位数
当n%2==0,则x,y的位数上不会产生差
当n%2!=0,则x,y的位数上会产生差,这个时候为了平衡x,y位数上的差
下一次就要将数值大的,分配给差更小的上
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int main()
{
int t;
cin >> t;
while (t--)
{
int n;
cin >> n;
string str = to_string(n);
int len = str.length();
int cnt = 0, x = 0, y = 0;
int pos = 0;
while (pos <= len - 1)
{
int wn = str[pos] - '0';
if (wn % 2 == 0)
{
x = x * 10 + wn / 2;
y = y * 10 + wn / 2;
}
else
{
if (cnt >= 0)
{
x = x * 10 + (wn + 1) / 2;
y = y * 10 + wn / 2;
cnt = -1;
}
else
{
x = x * 10 + wn / 2;
y = y * 10 + (wn + 1) / 2;
cnt = 1;
}
}
/* cout << x << " " << y << endl; */
pos++;
}
cout << x << " " << y << endl;
}
return 0;
}
《C. Matching Numbers》

这道题从数学角度上先想:
我想要求出s1
n*s1+1+..+n-1=n*s1+n(n-1)/2=(1+2n)2n/2
得到 s1=3n+3/2
可知n必须为奇数,否则无解
然后呢?
看了题解才知道,然后是不断测试样例同时多尝试几个数据
在我写的时候我试到了n=3,n=5,然后做实没每找到数据的规律
其实再尝试一个n=7就可以得出规律了
n=3
1 2 3 4 5 6
s1=6
1+5 3+4 2+6
n=5
1 2 3 4 5 6 7 8 9 10
s1=9
1+8 3+7 5+6 2+10 4+9
其实这里就可以看出来了,前面的数都先将奇数加完,然后在偶数
n=7
1 2 3 4 5 6 7 8 9 10 11 12 13 14
s1=12
1+11 3+10 5+9 7+8 2+14 4+13 6+12
也就是上面的规律了

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int main()
{
int t;
cin >> t;
while (t--)
{
int n;
cin >> n;
if (n % 2 == 0)
cout << "No" << endl;
else
{
cout << "Yes" << endl;
int k = (3 * n + 3) / 2;
int i = 1;
for (int j = k - i; i <= j; j--, i += 2)
{
cout << i << " " << j << endl;
k++;
}
for (int j = 2; j <= i - 2; j += 2)
{
cout << j << " " << k - j << endl;
k++;
}
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号