树形dp

大佬博客

　　由于树形dp种类繁多，而且大佬博客中总结的很好，这里我就只记录下我写到的树形dp

　

《F - Components》

　　

 

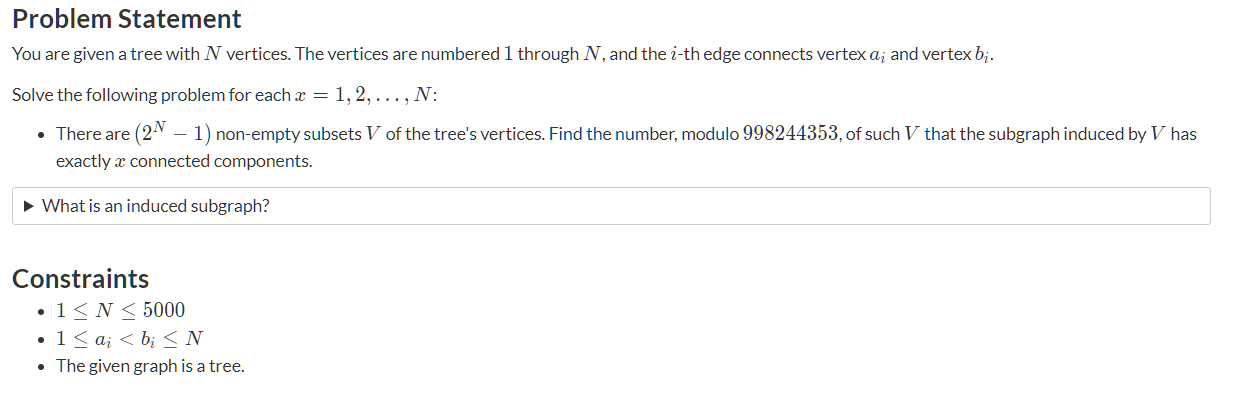
 简单的来说就是：

　　给一颗有n个节点的树，因为对于有n个节点的树，其n个节点有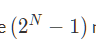个点集

 

 

　　现在问：由这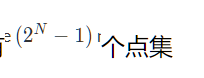，每个点集会形成h个连通分量

 

 

　　　　　　求连通分量为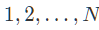时，所对应的点集个数

 

 

 

　

 

 当根u，其下有多个子树，我们从左到右枚举这些子树，

然后将其情况与根u的dp数组合并（即状态合并）

合并时，如图中描述的：

　　

 

 

 

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 5001, mod = 998244353;
vector<int> sides[N];
// dp[u][i][0/1]:表示以u为根节点的子树，当1时，u在点集中，当0时，u不在点集中
// 而且形成的连通分量的数量恰好为i的方案数
int n;
vector<vector<vector<int>>> dp(N, vector<vector<int>>(N, vector<int>(2)));
int dfs(int u, int f)
{
    dp[u][1][1] = 1, dp[u][0][0] = 1;
    // nows为当前以u为根节点的子树中最大能够形成的连通分量的数
    // sons为某一子树中最大能够形成的连通分量的数
    int nows = 1, sons;
    for (int i = 0; i < sides[u].size(); i++)
    {
        int to = sides[u][i];
        if (to == f)
            continue;
        sons = dfs(to, u);
        vector<vector<int>> t(n + 1, vector<int>(2));
        // l是枚举当前以u为根节点的子树能够形成连通分量为l
        // r是枚举u的其中一个子树能够形成连通分量为r
        for (int l = 0; l <= nows; l++)
            for (int r = 0; r <= sons; r++)
            {
                t[l + r][0] = (t[l + r][0] +
                               (ll)dp[u][l][0] * (dp[to][r][1] + dp[to][r][0]) % mod) %
                              mod;
                t[l + r][1] = (t[l + r][1] +
                               (ll)dp[u][l][1] * dp[to][r][0] % mod) %
                              mod;
                if (l + r - 1 >= 0)
                    t[l + r - 1][1] = (t[l + r - 1][1] +
                                       (ll)dp[u][l][1] * dp[to][r][1] % mod) %
                                      mod;
            }
        nows += sons;
        dp[u].swap(t);
    }
    return nows;
}
int main()
{
    cin >> n;
    for (int i = 1; i <= n - 1; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        sides[a].push_back(b), sides[b].push_back(a);
    }
    dfs(1, -1);
    for (int i = 1; i <= n; i++)
        cout << (dp[1][i][0] + dp[1][i][1]) % mod << endl;
    return 0;
}