2023牛客寒假算法基础集训营2
《重点考察容斥原理的题目》
《L. Tokitsukaze and Three Integers》
可以看的出：
n很小，首先考虑暴力的方法：
我们可以用两层for循环，将（ai*aj）%p 会等于什么求出来
然后再用两层for循环枚举 x 和 ak
看一下有多少个（ai*aj）%p 会对应上 (x-ak+p)%p
(这里x-ak+p，写成这样是防止负数的产生)
上面是完全不考虑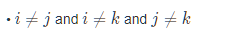 
这个条件的情况
上面的暴力，会导致在枚举ak的时候，可能ai*aj中：ai==ak 或者 aj==ak
要解决这个情况也很简单：
只要ans-= (ai*aj中ai==ak这种情况的个数+ai*aj中aj==ak这种情况的个数）
我们可以用一个数组d[i][x]表示在有ai参加运算的情况下，ai*另一个数=x的个数
那么ans-=d[k][(ai*aj)%p]即可
d[i][x]在两层for循环枚举ai和aj的时候可以处理：
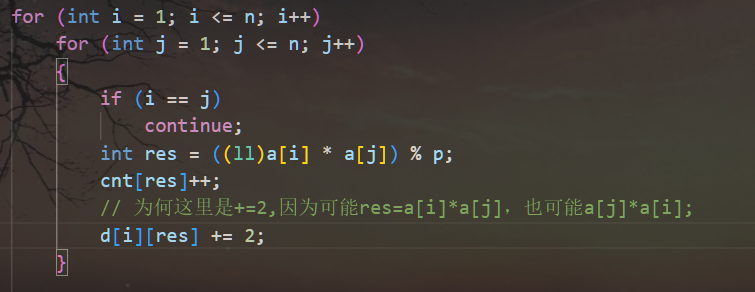
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 5001;
int n, p, a[N];
// cnt[x]:表示在a[]中有多少个（ai*aj）%p（i!=j）==x
// d[i][x]:表示有多少个是ai参与了组成了x
int cnt[N], d[N][5000];
int main()
{
cin >> n >> p;
for (int i = 1; i <= n; i++)
{
int num;
scanf("%d", &num);
a[i] = num % p;
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
{
if (i == j)
continue;
int res = ((ll)a[i] * a[j]) % p;
cnt[res]++;
// 为何这里是+=2,因为可能res=a[i]*a[j]，也可能a[j]*a[i];
d[i][res] += 2;
}
for (int x = 0; x <= p - 1; x++)
{
ll ans = 0;
for (int k = 1; k <= n; k++)
{
int res = (x - a[k] + p) % p;
ans += cnt[res] - d[k][res];
}
cout << ans << " ";
}
cout << endl;
return 0;
}
《Tokitsukaze and a+b=n (hard)》
像这样题目一开始给出很多个区间，十分难想：
我们可以将 区间全部下压到一条x轴上
只要x轴上的数（num）在某个区间上，那么cnt[num]++
最终这个cnt[num]表示：
num在多少个区间出现过
这里要求出cnt[]数组来显然不能用暴力，而是要点技巧：
对于给一段连续区间上的全部数进行+操作的快捷技巧：
差分
我们设置一个差分数组ca[],然后对于区间[l,r]
ca[l]++,ca[r+1]--
再对差分数组求一边前缀和，即可得cnt[]数组
这个时候如果不考虑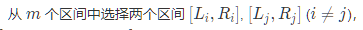
这个条件
那么答案就是：c[a]*c[n-a]
a用for循环枚举
这个含义就是从c[a]个区间选出数a来，再从c[n-a]区间选出数b来，a+b=n
但是我们要考虑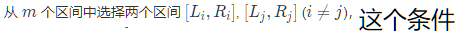
按照容斥原理：我们只要用ans-=(i==j,a+b==n的个数来即可)
即对于每一个区间，我们都要找到有多少个a+b==n的对数
这个其实就是Tokitsukaze and a+b=n (medium)的做法
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 4 * 1e5 + 2, p = 998244353;
int n, m;
ll ca[N];
ll solve(int l1, int r1, int l2, int r2)
{
ll l = l1, r = r1, nb = -1;
while (l <= r)
{
ll mid = (l + r) >> 1;
ll b = n - mid;
// 说明mid太大了
if (b < l2)
r = mid - 1;
else if (b > r2)
l = mid + 1;
else
{
nb = b;
break;
}
}
if (nb == -1)
return 0;
ll na = n - nb, ans = 0;
ans++;
ans += min(r1 - na, nb - l2);
ans += min(na - l1, r2 - nb);
return ans;
}
int main()
{
cin >> n >> m;
ll same = 0;
for (int i = 1; i <= m; i++)
{
int l, r;
cin >> l >> r;
// 处理相同区间中元素相加使得为n的方案对数
same = (same + solve(l, r, l, r)) % p;
ca[l]++, ca[r + 1]--;
}
// 来一遍前缀和，看一下每个数在多少个不一样的区间出现过
// 这里直接出鬼了，这里一定要写i<=N
// 而不能写i<=200000,但是题目数据写的明明是1<=l,r<=200000
for (int i = 1; i <= N; i++)
ca[i] = ca[i] + ca[i - 1];
ll all = 0;
for (int i = 1; i <= N; i++)
if (n >= i)
all = (all + (ca[i] * ca[n - i]) % p) % p;
cout << (all - same + p) % p << endl;
return 0;
}
《重点考察化繁为简，对每个值单独考虑求贡献的思路》
《Tokitsukaze and K-Sequence》
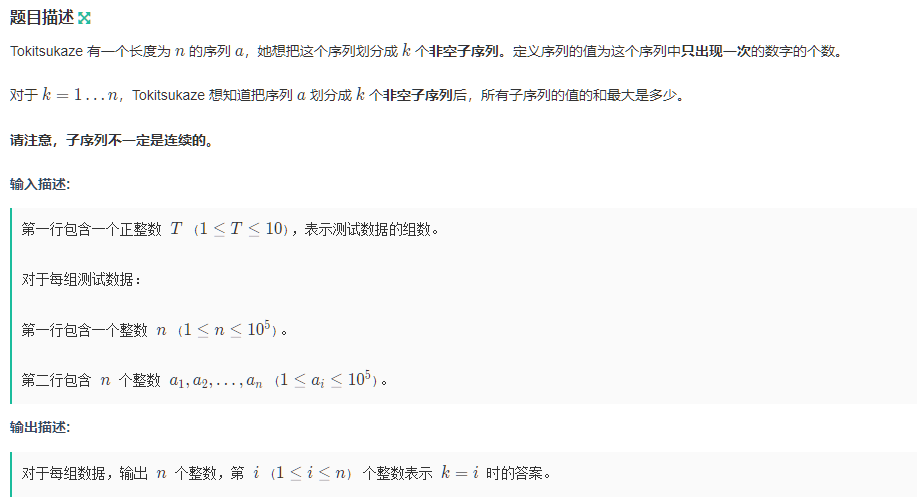
对于这道题，首先就有个想法：
既然在一个序列中只有出现一次的数才有贡献
为了使贡献值最大，假设有n个序列，对于同一个数，将其中一个放到一个序列中
如果还有剩余，那么将其余全部的个数放到最后一序列中
对于同一个数num，假设其有m个
对于序列只有
1个时：贡献为0
2个时：贡献为1
3个时：贡献为2
....
m-1个时：贡献为m-2
m个时：贡献为m
m+1个时：贡献为m+1
我们发现：
当序列个数n，n<m，那么贡献为n-1
当序列个数n，n==m，那么贡献为n
当序列个数n，n>m，那么贡献为n
于是这道题的方案也就出来了：
我们首先可以对原序列a，统计其中数num,到底出现了多少次cnt[num]
同时找到不同的num有多少个:sum
我们枚举序列个数:i
对于cnt[num]<=i的 ans+=cnt[num],sum--
对于剩余cnt[num]>i的 ans+=sum*(i-1)
#include <iostream>
#include <algorithm>
#include <cstring>
#include <set>
using namespace std;
const int N = 1e5 + 2;
int cnt[N], n;
void solve()
{
cin >> n;
memset(cnt, 0, sizeof(cnt));
for (int i = 1; i <= n; i++)
{
int num;
scanf("%d", &num);
cnt[num]++;
}
multiset<int> s;
for (int i = 1; i <= 100000; i++)
if (cnt[i])
s.insert(cnt[i]);
int ans = 0, sum = s.size();
auto j = s.begin();
for (int i = 1; i <= n; i++)
{
while (j != s.end() && *j <= i)
{
ans += *j;
j++;
sum--;
}
cout << ans + (long long)(i - 1) * sum << endl;
}
}
int main()
{
int t;
cin >> t;
while (t--)
solve();
return 0;
}
《Tokitsukaze and Musynx》
（我在这里先吐槽一下：这个题目意思也太难看懂了，还是看样例看懂意思的）
这道题的题意为：
划分出5个区间：
（-INF，a）,[a,b),[b,c),[c,d],(d,+INF)
每个区间有对于的值v1,v2,v3,v4,v5
给n个音符，开始每个音符在的区间为xi(1<=i<=n)
我们可以个这n个音符的位置同时+上h
问全部音符的值的和最大为多少
首先暴力想的话只要枚举h这一条道路了吧：
但是会超时
但是真的有必要每一个h都枚举吗？
这里我们专门拿出一个音符来分析：
假设区间为：
（-INF，1）【1，5）【5，10）【10,16】（16，+INF）
假设有5个音符，初始位置为：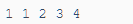
对于第一个音符：
其初始在区间v2上
我们想将其移动到区间v1,那么至少要h=-1
这个时候贡献值的变化为：ans-=v2,ans+=v1
对于h<=-1,贡献值不再变化
我们想将其移动到v3,那么至少h=+4
这个时候贡献值的变化为：ans-=v2,ans+=v3
对于4<=h<=8,贡献值不再变化
...........
移动到其余区间也如此分析：
我们可知：我们并不需要枚举每一个h
只要枚举使得音符贡献值变化的h即可
这样的h，对于一个音符来说只有4个
对于n个音符来说也只有4*n个
我们收集起这些h，然后枚举，然后记录贡献值的变化
为了方便操作，可以初始给每一个音符的位置都-=INF,即使他们都有处于v1区间
#include <iostream>
#include <cstring>
#include <algorithm>
#include <map>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 2 * 1e5 + 2;
const ll INF = 1e10;
ll arr[N], n, pos[5], vs[6];
void init()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
ll num;
scanf("%lld", &num);
arr[i] = num - INF;
}
for (int i = 1; i <= 4; i++)
{
ll num;
scanf("%lld", &num);
if (i == 4)
num++;
pos[i] = num;
}
for (int i = 1; i <= 5; i++)
scanf("%lld", &vs[i]);
}
void solve()
{
init();
ll ans = vs[1] * n, res = ans;
map<ll, vector<int>> s;
for (int i = 1; i <= n; i++)
// 对于每一个音符单独考虑贡献，这里我们的h并不用全部枚举
// 而是只要枚举首个能够改变某一个音符的h
// 这样的h最多有4*n个
for (int j = 1; j <= 4; j++)
{
ll h = pos[j] - arr[i];
s[h].push_back(j + 1);
// 这个是需要模拟样例才能明白的操作
// 简单来说，如从v1->v2,想要迭代ans,我们必须先-vs[1]，再+vs[2]
s[h].push_back(-j);
}
for (auto i = s.begin(); i != s.end(); i++)
{
vector<int> t = i->second;
for (int j = 0; j < t.size(); j++)
{
if (t[j] > 0)
ans += vs[t[j]];
else
ans -= vs[-t[j]];
}
res = max(ans, res);
}
cout << res << endl;
}
int main()
{
int t;
cin >> t;
while (t--)
solve();
return 0;
}
《Tokitsukaze and Gold Coins (easy)》
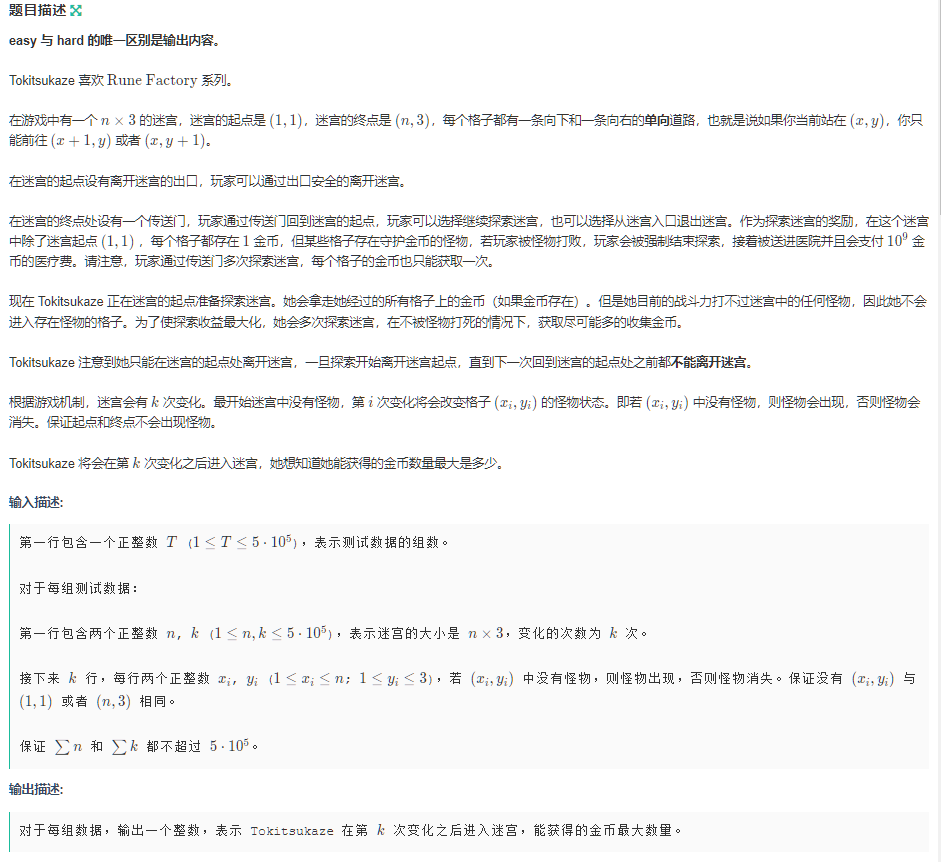
这道题的难点在于：
我如何判断某个点上的金币是否拿了没有，如何统计金币？
这里给出两种做法：
1.dfs（y,x）:
表示从点（x，y）能够到达终点，则说明这个点（x,y）处的金币能够拿
用dfs则要进行剪枝，避免超时
具体操作是，如果已知某个点能到或者不能到终点，这个时候就可以直接返回了
不必再搜下去
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 5 * 1e5 + 2;
int n, k, st[N][4];
vector<vector<int>> g(N + 1, vector<int>(4));
int dy[] = {0, 1}, dx[] = {1, 0};
int ans;
bool dfs(int y, int x)
{
if (y == n && x == 3)
return true;
if (st[y][x] == 1)
return true;
bool flag = false;
for (int i = 0; i <= 1; i++)
{
int ny = y + dy[i], nx = x + dx[i];
if (ny < 1 || ny > n || nx < 1 || nx > 3)
continue;
if (st[ny][nx] == -1 || g[ny][nx])
continue;
if (dfs(ny, nx))
{
if (st[y][x] == 0)
ans++;
st[y][x] = 1;
flag = true;
}
}
if (!flag)
{
st[y][x] = -1;
return false;
}
return true;
}
void solve()
{
cin >> n >> k;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= 3; j++)
{
g[i][j] = 0;
st[i][j] = 0;
}
for (int i = 1; i <= k; i++)
{
int y, x;
scanf("%d%d", &y, &x);
if (g[y][x])
g[y][x] = 0;
else
g[y][x] = 1;
}
ans = 0;
dfs(1, 1);
cout << ans << endl;
}
int main()
{
int t;
cin >> t;
while (t--)
solve();
return 0;
}
2.bfs的写法：
需要从起始点来一遍bfs到终点，看一下起点到终点会走哪些路
再从终点到起点再来一遍bfs到起始点，看一下终点到起点会走哪些路
两边bfs重叠走的路，就是正确的路，这些路上的金币都拿下
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 5 * 1e5 + 2;
int n, k;
bool st[N][4][2];
vector<vector<int>> g(N + 1, vector<int>(4));
int dy[] = {0, 1}, dx[] = {1, 0};
int by[] = {-1, 0}, bx[] = {0, -1};
void bfs(int y, int x, int s)
{
queue<PII> q;
q.push({y, x});
while (q.size())
{
PII t = q.front();
q.pop();
st[t.first][t.second][s] = true;
for (int i = 0; i < 2; i++)
{
int ny, nx;
if (s == 0)
ny = t.first + dy[i], nx = t.second + dx[i];
else
ny = t.first + by[i], nx = t.second + bx[i];
if (ny < 1 || ny > n || nx < 1 || nx > 3)
continue;
if (st[ny][nx][s] || g[ny][nx])
continue;
q.push({ny, nx});
}
}
}
void solve()
{
cin >> n >> k;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= 3; j++)
{
g[i][j] = 0;
for (int k = 0; k <= 1; k++)
st[i][j][k] = false;
}
for (int i = 1; i <= k; i++)
{
int y, x;
scanf("%d%d", &y, &x);
if (g[y][x])
g[y][x] = 0;
else
g[y][x] = 1;
}
bfs(1, 1, 0);
bfs(n, 3, 1);
int ans = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= 3; j++)
{
if (st[i][j][0] == st[i][j][1] && st[i][j][0])
ans++;
}
if (ans > 0)
cout << ans - 1 << endl;
else
cout << ans << endl;
}
int main()
{
int t;
cin >> t;
while (t--)
solve();
return 0;
}
《Tokitsukaze and Function》
这道题细节很多，要小心：
设g(x)=n/x+x
设f*(x)=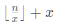
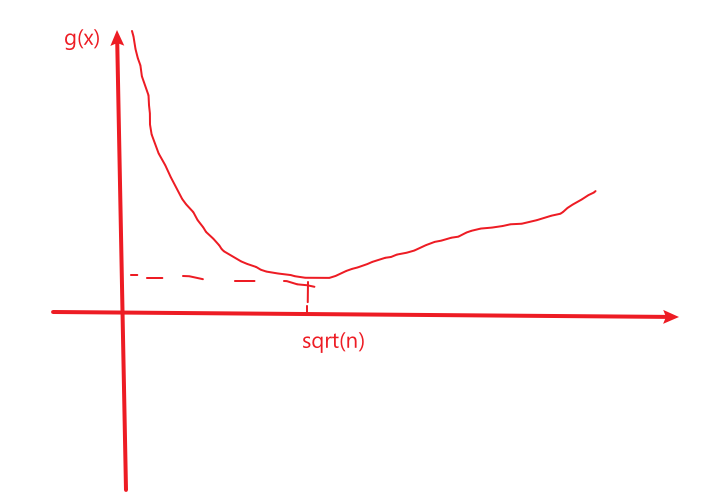
f*(x)<=g(x)
g(x)-f*(x)<=1
可以猜想出f*(x)的图像是在g（x）图像下方，
十分贴近g(x)的不连续的点图（因为f*(x)的x只取整正数）
但是f*(x)的最小值点也一定还是在x=sqrt(x)的附近，
同理f(x)的最小值点也一定还是在x=sqrt(x)的附近，
我们在确定最小值后，为了寻求最小的x使得f(x)最小
我们可以对最小值点r=minx,l=l
进行二分
注意minx不在【l,r】的情况
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
typedef long long ll;
void solve()
{
ll n, l, r;
cin >> n >> l >> r;
ll minx = sqrt(n);
if (minx < l || minx > r)
{
ll ansl = n / l + l - 1, ansr = n / r + r - 1;
if (ansl <= ansr)
cout << l << endl;
else
{
// 注意在r这里也要找到最小的对应的下标值
ll el = l, er = r, ans;
while (el <= er)
{
ll mid = (el + er) >> 1;
if (n / mid + mid - 1 <= ansr)
{
ans = mid;
er = mid - 1;
}
else
el = mid + 1;
}
cout << ans << endl;
}
return;
}
ll pos0 = max(l, (ll)sqrt(n) - 1), pos1 = sqrt(n), pos2 = min(r, (ll)sqrt(n) + 1);
ll ans0 = n / pos0 + pos0 - 1, ans1 = n / pos1 + pos1 - 1, ans2 = n / pos2 + pos2 - 1;
ll el = l, er, ans, stand;
if (ans0 <= ans1 && ans0 <= ans2)
er = pos0, stand = ans0;
else if (ans1 <= ans0 && ans1 <= ans2)
er = pos1, stand = ans1;
else if (ans2 <= ans0 && ans2 <= ans1)
er = pos2, stand = ans2;
while (el <= er)
{
ll mid = (el + er) >> 1;
if (n / mid + mid - 1 <= stand)
{
ans = mid;
er = mid - 1;
}
else
el = mid + 1;
}
cout << ans << endl;
}
int main()
{
int t;
cin >> t;
while (t--)
solve();
return 0;
}
浙公网安备 33010602011771号