Codeforces Round #845 (Div. 2) and ByteRace 2023

《B. Emordnilap》

数学，思维

 

 

 题意：

　　给定一个由1~n组成序列，然后将这序列复制，反转，再放到原序列的末尾，

　　得到新的序列（设为s）

　　问s的逆序对个数

 

当时我写的时候，序列方向搞错了ORZ, 但是再来看题解，题解的方法比我简单多了：

　　

　　首先：我们可以将逆序对的来源分成3处

　　

 

 

 　　第3处的逆序对数为n(n-1)/2

　　为啥？因为s1中的1在s2处有0个<1的

　　　　　　   s1中的2在s2处有1个<2的

　　　　　　   s1中的3在s2处有2个<3的

　　　　　　   .................

　　从1~n共有0+1+2+......+n=n*(n-1)/2

 

　　假设s1处的逆序对个数为num,那s2处的逆序对为多少？

　　

　　s2是s1的逆，那么在s1中是逆序对的，在s2中就是顺序对，反之也成立

　　一个长度的为n，由1~n排列而成的序列，总共有n(n-1)/2种对关系

 

　　则上面的答案就是n（n-1）/2-num

　　

　　所以一个序列的逆序对数为n(n-1),同理所有序列的逆序对个数为n*(n-1)

　　总共有n!个序列

　　则答案就是 n!n（n-1）

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const ll mod = 1e9 + 7;
ll J[100002];
void solve()
{
    ll n;
    cin >> n;
    /* cout << J[n] << endl; */
    cout << (J[n] * ((n + 2) * (n - 1) / 2) % mod) % mod << endl;
}
int main()
{
    int t;
    cin >> t;
    ll n = 1;
    for (ll i = 1; i <= 1e5; i++)
    {
        J[i] = (n * i) % mod;
        n = (n * i) % mod;
    }
    while (t--)
        solve();
    return 0;
}

 

 

 

《C. Quiz Master》

 

 双指针

写这道题的时候我首先就遇到了一个致命的问题：

　　假设我选出了u个学生，我该如何判断这u个学生是否可以组成最佳团队？

　　暴力？对于每个学生都在1~m上看一遍？

　　假设这个u很大不就超时了嘛

　　

　　考虑优化，为啥超时，因为对于每个学生我们都看了一遍1~m

　　有没有啥方法对于一学生不用看1~m

　　假设某一个学生的聪明度为sm,我们想在1~m中找到sm的因子，真的有必要1~m扫一遍吗？

　　

　　其实我们可以预处理出来在1~m中对于任意一个数j，j的全部因子，在O（nlog（n））的时间复杂度之内

　　

 

 　　   

 

　　这个方法很巧妙，避免了n^2

　　

　　然后回到上面的问题，对于一个团队，我们只要对于其中的学生，

　　枚举这个学生聪明度的因子，看一下这些因子中是否有1~m中的数

　　最终可以知道1~m中的数是否被全部枚举到

　　

　　在回到题目的本来的问题：

　　　　如何求出一个合法的团队，要求团队中最大聪明度和最小聪明度的差最小

　　

　　明显我们关系的只是最大聪明度和最小聪明度，如果定下了最下聪明度或最大聪明度，

　　我们可以让最大聪明度尽量小 或 最小聪明度尽量大，其他在这个范围内的聪明度随意

　　

　　这么想的话是不是有个暴力的想法出来了：

　　　　我们对原数组排序（从小到大）

　　　　我们枚举要定下的最小聪明度，然后不断增大最大聪明度，一旦

　　　　最小聪明度~最大聪明度这个范围内，最成的团队可以使1~m的数都得到

　　　　那么成功，记录一下，然后换下一个最小聪明度

　　但是这样的时间复杂度是O（n^2）

 

　　对于有序的数组，求两点之间的关系可以用双指针将O（n^2）优化到O(n)

　　我们可以定义两个指针：l，r

　　开始l=r=1

　　然后r++，自到，1~m的数都得到，记录下答案

　　然后l++,即想要向r靠近，减少差的值

　　l变动了，其下能够整除的数也会变化，我们再重复上述步骤

　　最终得到答案

　　

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
const int N = 1e5 + 2;
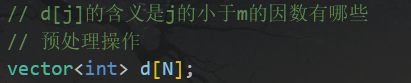
// d[j]的含义是j的小于m的因数有哪些
// 预处理操作
vector<int> d[N];
int n, m;
int a[N], cnt[N], s = 0;
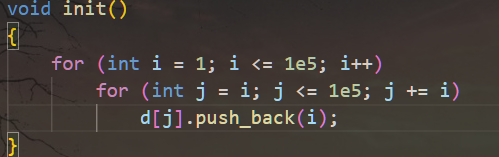
void init()
{
    for (int i = 1; i <= 1e5; i++)
        for (int j = i; j <= 1e5; j += i)
            d[j].push_back(i);
}
void solve()
{
    memset(cnt, 0, sizeof(cnt));
    s = 0;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    sort(a + 1, a + n + 1);
    int ans = 1e9;
    for (int l = 1, r = 1; r <= n; r++)
    {
        for (auto x : d[a[r]])
        {
            if (x > m)
                break;
            if (cnt[x] == 0)
                s++;
            cnt[x]++;
        }
        while (s == m)
        {
            ans = min(ans, a[r] - a[l]);
            for (auto x : d[a[l]])
            {
                if (x > m)
                    break;
                if (cnt[x] > 0)
                    cnt[x]--;
                if (cnt[x] == 0)
                    s--;
            }
            l++;
        }
    }
    if (ans >= 1e9)
        cout << -1 << endl;
    else
        cout << ans << endl;
}
int main()
{
    init();
    int t;
    cin >> t;
    while (t--)
        solve();
    return 0;
}