字符串处理
《面对字符串输入的情况》

想这个输入格式我该如何输入?
这样即可:
scanf("%d:(%d)", &s, &cnt);
《字符串哈希》
对于字符串str长度为n,可以在O(n)的时间内解决字符串str上任意一段区间的子串与其他字符串是否相同

我们用这个方法就可以实现:

再来看下面一个要求:


这道题我们实际上用KMP才更好,如果要用字符串哈希该如何写?

那么用字符串哈希如何快速得到字符串s各个区间的值来判断他们是否相等?
设字符串s为:x1 x2 x3 ......xn
那么我们各个阶段的哈希值为:
h[i]=h[i-1]*p+xi
有没有发现这个h[i]有点像前缀和一样?
对于字符串区间[l,r]
他们的h[l,r] = h[r]- h[l-1] * p^(r-l+1);
关于这点如何解释呢?
正如十进制下的:123 456 123
如果我想知道这个十进制数 [7,9]区间的值是多少该如何求?
我们用眼睛一看就知道为:123
其实 h[9]= [1,9]区间的值为:1*10^8+2*10^7+....+1*10^2+2*10^1+3*10^0
h[6]= [1,6]区间的值为:1*10^5+....+6*10^0
h[9]-h[6]*10^3== 123 456 123 - 123 456 000 = 123
就求出来了
注意写代码时h[]记得用上 unsigned long long 其在溢出时有自动mod 2^64的效果
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef unsigned long long ull;
const int p = 131, N = 1e6 + 2;
ull ps[N], h[N];
char str[N];
bool check(int len, int n)
{
if (len == n)
return true;
ull t = h[len] - h[0] * ps[len + 1];
int l = len + 1, r = l + len - 1;
while (r <= n)
{
ull tt = h[r] - h[l - 1] * ps[r - l + 1];
if (t != tt)
return false;
l = r + 1;
r = l + len - 1;
}
return true;
}
int main()
{
ps[0] = 1;
for (int i = 1; i <= N; i++)
ps[i] = ps[i - 1] * p;
while (scanf("%s", str))
{
if (str[0] == '.')
break;
int n = strlen(str);
h[0] = 0;
for (int i = 0; i < n; i++)
h[i + 1] = h[i] * p + str[i];
for (int i = 1; i <= n; i++)
{
if (n % i)
continue;
if (check(i, n))
{
cout << n / i << endl;
break;
}
}
}
return 0;
}
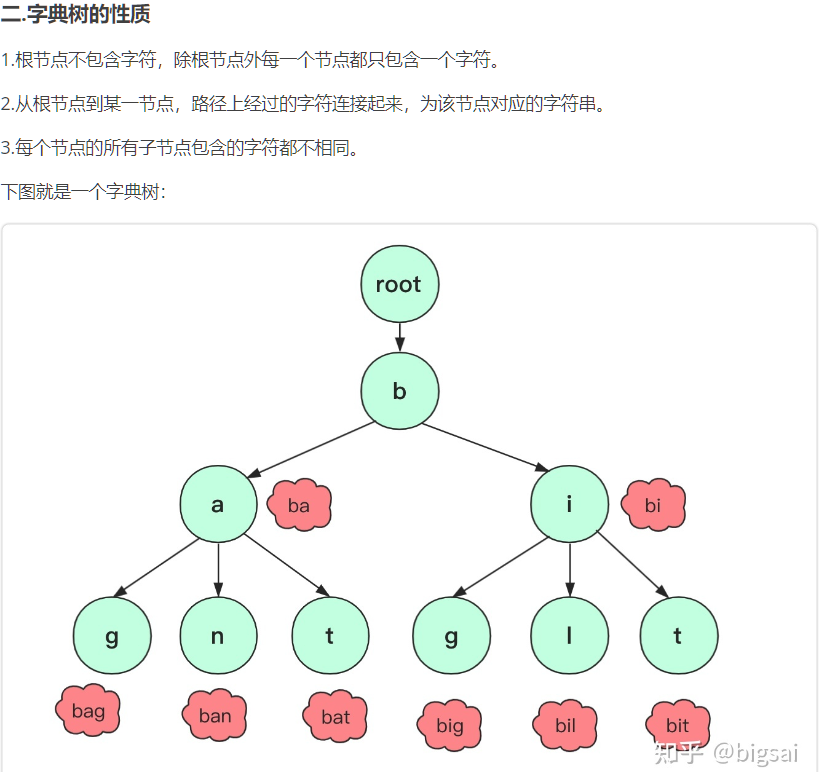
《trie树(字典树)(前缀树)》
正如名字所言:对于总共最大输入n个字符串长度,其可以在O(n)的时间内建立出字符串树处理
可以解决字符串关于前缀的问题

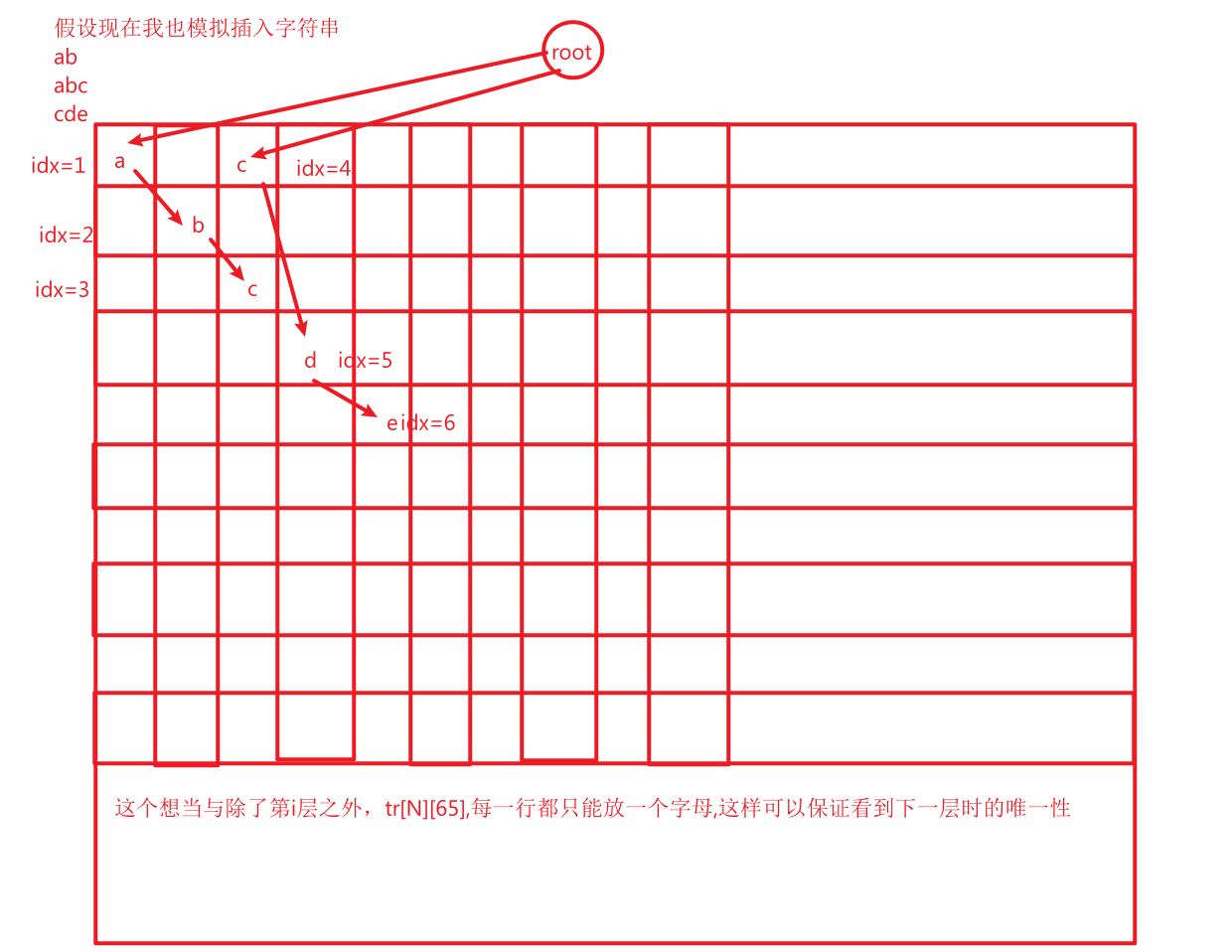
在具体实现的时候我们最方便的使用一个二维数组实现的:设这个数组的名称为tr[N][65]
N代表输入字符串最大的总长度,65是可以处理‘a’,'A','0',小写,大写,数字这样的字符串,具体转换如下:
int get(char c)
{
if (c >= '0' && c <= '9')
return c - '0';
else if (c >= 'A' && c <= 'Z')
return c - '0' - 7;
else
return c - '0' - 13;
}
这样让 '0'-‘9‘ 为 0-9
'A'-'Z'为 10-35
‘a’-'z'为 36-61
与tr[N][65]相配套工作的是类似指针效果的int idx
他有标记是否字符存在的效果和指向下一个字符的效果:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
using namespace std;
const int N = 65, M = 3 * 1e6 + 2;
int tr[M][N], idx = 0, cnt[M];
int get(char c)
{
if (c >= '0' && c <= '9')
return c - '0';
else if (c >= 'A' && c <= 'Z')
return c - '0' - 7;
else
return c - '0' - 13;
}
void insert(string str)
{
// 表示一开始从根节点开始
int q = 0;
for (int i = 0; i < str.length(); i++)
{
int t = get(str[i]);
if (!tr[q][t])
tr[q][t] = ++idx;
q = tr[q][t];
// 用来记录有多少个字符串的前缀经过这个
cnt[q]++;
}
}
int query(string str)
{
int q = 0, ans = 0;
for (int i = 0; i < str.length(); i++)
{
int t = get(str[i]);
q = tr[q][t];
if (q == 0)
return 0;
ans = cnt[q];
}
return ans;
}
int main()
{
/* cout << int('A') << " " << int('a') << " " << int('0') << endl; */
/* cout << get('Z') << " " << get('z') << endl; */
int t;
cin >> t;
while (t--)
{
int n, m;
cin >> n >> m;
// 大数组用memset会超时。。。。。。
/* memset(cnt, 0, sizeof(cnt));
memset(tr, 0, sizeof(tr)); */
for (int i = 0; i <= idx; i++)
for (int j = 0; j <= N - 1; j++)
tr[i][j] = 0;
for (int i = 0; i <= idx; i++)
cnt[i] = 0;
idx = 0;
for (int i = 1; i <= n; i++)
{
string str;
cin >> str;
insert(str);
}
for (int i = 1; i <= m; i++)
{
string str;
cin >> str;
cout << query(str) << endl;
}
}
return 0;
}
《KMP》
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e6 + 2;
//模式串是去匹配的字符串,文本串是被匹配的字符串
//p[N]也可以称为next[N]
//p[j]表示:模式串区间1~j的字符串最长公共前缀后缀的长度
//也可以表示 当模式串在第j+1个字符与文本串不匹配的时候
//在模式串下一个尝试与文本串中不匹配的字符进行的匹配的是第p[j]+1个字符
int p[N];
char str1[N], str2[N];
int main()
{
scanf("%s%s", str1 + 1, str2 + 1);
int len1 = strlen(str1 + 1), len2 = strlen(str2 + 1);
p[1] = 0;
// j是模式串
int j = 0;
for (int i = 2; i <= len2; i++)
{
while (j > 0 && str2[i] != str2[j + 1])
j = p[j];
if (str2[i] == str2[j + 1])
j++;
p[i] = j;
}
j = 0;
for (int i = 1; i <= len1; i++)
{
while (j > 0 && str1[i] != str2[j + 1])
j = p[j];
if (str1[i] == str2[j + 1])
j++;
if (j == len2)
{
cout << i - len2 + 1 << endl;
j = p[j];
}
}
for (int i = 1; i <= len2; i++)
cout << p[i] << " ";
cout << endl;
return 0;
}
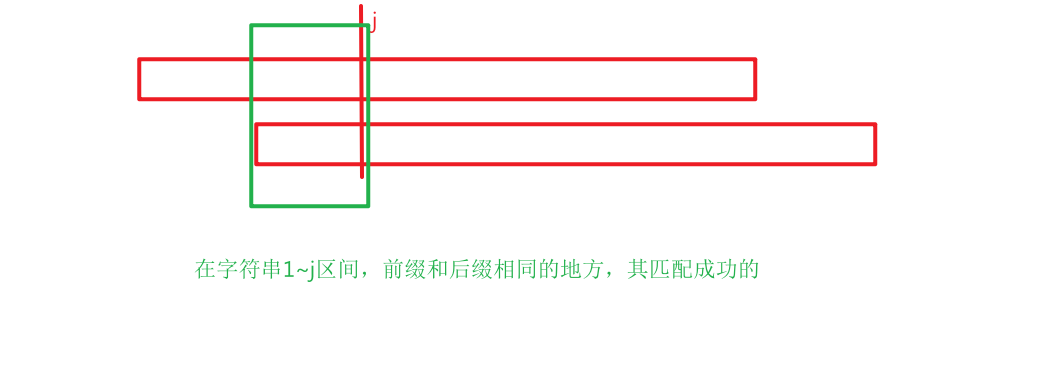

结论就是:如果字符串是由某循环子串不断循环拼接而成,那么其KMP的next[n]
有: 这个字符串最小循环子串的长度为n-next[n];


 浙公网安备 33010602011771号
浙公网安备 33010602011771号