单调栈和单调队列

《单调栈》

#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
using namespace std;
const int N = 3 * 1e6 + 2;
int n;
struct node
{
    int num, pos;
} a[N];
int ans[N];
stack<struct node> heap;
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i].num);
        a[i].pos = i;
    }
    for (int i = 1; i <= n; i++)
    {
        while (heap.size() && heap.top().num < a[i].num)
        {
            ans[heap.top().pos] = i;
            heap.pop();
        }
        heap.push(a[i]);
    }
    while (heap.size())
    {
        ans[heap.top().pos] = 0;
        heap.pop();
    }
    for (int i = 1; i <= n; i++)
        cout << ans[i] << " ";
    cout << endl;
    return 0;
}

 

《单调队列》

可以解决类似滑动窗口这样的问题：

 

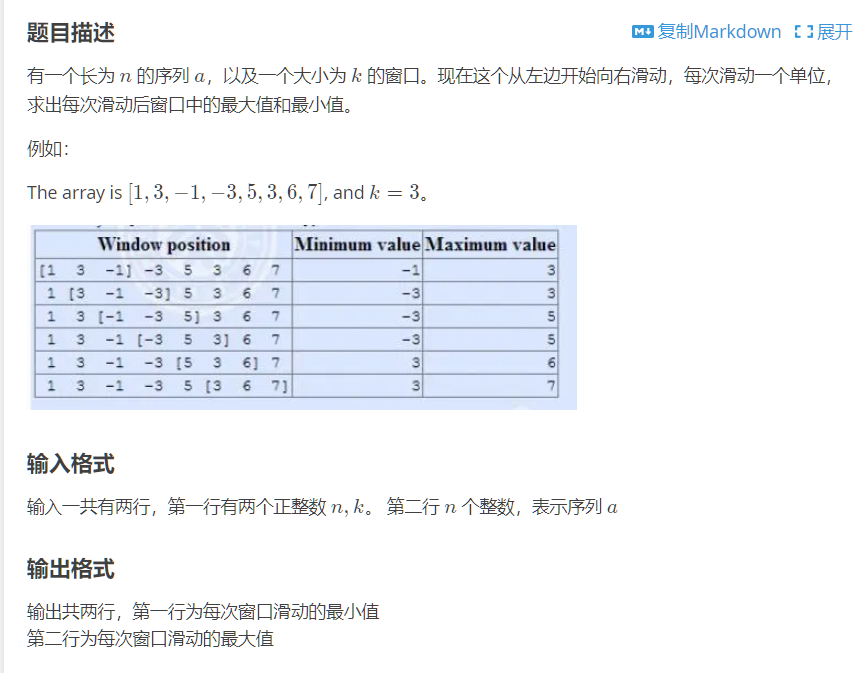
 很明显：如果用最朴素的每一个新区间就排序，绝对会超时

观察发现：减少的每次都是最左端的数，增加的每次都是最右端的数，那么我们可不可以利用这个性质去作一些优化？

 

我们发现：当我们用单调栈的思想，比如维护区间数的单调递增

在区间最左边的数，要不就在单调栈的栈底，要不就不在栈中

因为区间最左边的数，是最先进入栈的，如果其值是最小的，那么其就在单调栈的栈底

否则其就一定会被后面更小的数挤出栈中

 

这个性质为我们当减少的每次都是最左端的数，提供了一个很好维护单调栈的条件，即每次我们只要看一下单调栈的栈底是不是最左端的数

如果是当最左端的数被移出区间时，我们可以将单调栈中相应的数移出

再加入新数，再看单调栈栈底即为最小值

 

看区间最大值同理。

设计到看栈的底部和top,用双端队列实现

 1 #include <iostream>
 2 #include <algorithm>
 3 #include <cstring>
 4 #include <stack>
 5 #include <vector>
 6 #include <queue>
 7 #include <deque>
 8 using namespace std;
 9 const int N = 1e6 + 2;
10 struct node
11 {
12     int pos, num;
13 };
14 // maxh维护从小到大，minh维护从大到小
15 deque<struct node> maxh, minh;
16 int a[N], mina[N], maxa[N];
17 void keepMax(node t)
18 {
19     while (maxh.size() && maxh.back().num > t.num)
20         maxh.pop_back();
21     maxh.push_back(t);
22 }
23 void keepMin(node t)
24 {
25     while (minh.size() && minh.back().num < t.num)
26         minh.pop_back();
27     minh.push_back(t);
28 }
29 int main()
30 {
31     int n, k;
32     cin >> n >> k;
33     for (int i = 1; i <= n; i++)
34         scanf("%d", &a[i]);
35     for (int i = 1; i <= 1 + k - 1; i++)
36     {
37         node t = {i, a[i]};
38         keepMax(t);
39         keepMin(t);
40     }
41     for (int l = 1, r = l + k - 1; r <= n; l++, r++)
42     {
43         if (l != 1)
44         {
45             node lose = {l - 1, a[l - 1]};
46             node add = {r, a[r]};
47             if (maxh.front().pos == lose.pos)
48                 maxh.pop_front();
49             if (minh.front().pos == lose.pos)
50                 minh.pop_front();
51             keepMax(add);
52             keepMin(add);
53         }
54         mina[l] = maxh.front().num;
55         maxa[l] = minh.front().num;
56     }
57     for (int i = 1; i <= n - k + 1; i++)
58         cout << mina[i] << " ";
59     cout << endl;
60     for (int i = 1; i <= n - k + 1; i++)
61         cout << maxa[i] << " ";
62     cout << endl;
63     return 0;
64 }

 

posted @ 2022-12-30 19:04  次林梦叶  阅读(31)  评论(0)    收藏  举报