AtCoder Beginner Contest 282

《Make Bipartite 2》

思维，二分图

 

 这个简单图可以有两种情况：

　　1.全部点都通过边连起来，即连通分量只有一个，其自己

　　2.还有有些点没有全部连起来，即有多个连通分量

1.不管上面哪一种情况，如果对图跑一个二分图染色O（n+m）,如果染色失败，则都是返回0，因为这时，不管再连上那一边都不是二分图了

 

下面我们保证跑一个二分图染色O（n+m）,如果染色成功：

2.现在我们假设各个点之间都有边，即一共有n*(n-1)/2条边

　　　　（1）对于只有一个连通分量来说: 连上相同颜色的点的边和已经连好的边（m），都是使二分图不合法的，除此之外都是合法的

　　则假设这个连通分量上有w个白点，b个黑点，则不合法的边为 w*(w-1)/2+b*(b-1)/2+m条

　　则正确答案为ans=n*(n-1)/2-（w*(w-1)/2+b*(b-1)/2+m）；

　　　　（2）对于有多个连通分量来说：两个不同的连通分量上的任意点相连,都还是二分图

　　对于相同连通分量上的相同颜色的点相连是不合法的，同时已经连好的边（m）也是不合法的

于是：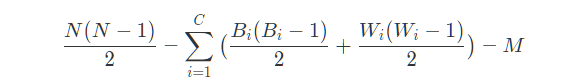

 

 

 这里循环相加的是各个连通分量上黑点相连的边数与白点相连的边数

 

即我们在写dfs跑二分图染色时，可以返回这个连通分量上黑点与白点的个数

 

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
const int N = 2 * 1e5 + 2;
typedef long long ll;
typedef pair<int, int> PII;
int color[N], n, m;
vector<int> sides[N];
PII dfs(int x, int c)
{
    PII p = {0, 0};
    color[x] = c;
    if (c == 1)
        p.first++;
    else
        p.second++;
    for (int i = 0; i < sides[x].size(); i++)
    {
        int j = sides[x][i];
        PII res;
        if (!color[j])
            res = dfs(j, -c);
        else if (color[j] == c)
            // 表示不构成二分图
            return {-1, -1};
        if (res.first == -1 && res.second == -1)
            return {-1, -1};
        else
        {
            p.first += res.first;
            p.second += res.second;
        }
    }
    return p;
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        sides[a].push_back(b), sides[b].push_back(a);
    }
    ll ans = (ll)n * (n - 1) / 2 - m;
    for (int i = 1; i <= n; i++)
    {
        if (!color[i])
        {
            PII p = dfs(i, 1);
            // p.first表示这个连通分量中染色白色的个数（color==1）,p.second 表示这个连通分量中染色黑色的个数；
            if (p.first == -1 && p.second == -1)
            {
                cout << 0;
                return 0;
            }
            ans -= (ll)p.first * (p.first - 1) / 2;
            ans -= (ll)p.second * (p.second - 1) / 2;
        }
    }
    cout << ans;
    return 0;
}

 《E - Choose Two and Eat One 》

最大生成树，思维

 

 

 首先这道题N很小，即使将全部气球之间的得分搞出来也就O（N*N）

然后题目描述当我们选择了一个气球时就要抛弃一个气球，另一个气球还可以用。

我们将气球看成点

将气球之间的得分看成边的权重

也就是所我们要从n*n的边中（每个点到其他各个点之间的边总共有n*n条），选出n-1条边（因为一旦选择了任意两个点之后，一定会有其中一个点不能再用了，最后真正选出的边为n-1条），这n-1条边可以连接上全部的点，同时权重之和是最大的

这不就是最大生成树吗？

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 502;
struct node
{
    int len;
    int from, to;
    bool operator<(const node &t) const
    {
        return len > t.len;
    }
} sides[N * N];
int arr[N], n, m, pos = 0;
int quick(int a, int b, int m)
{
    int ans = 1;
    while (b)
    {
        if (b & 1)
            ans = ((ll)ans * a) % m;
        b >>= 1;
        a = ((ll)a * a) % m;
    }
    return ans;
}
int h[N];
int find(int x)
{
    if (h[x] != x)
        h[x] = find(h[x]);
    return h[x];
}
ll Kruskal()
{
    int count = 1;
    ll ans = 0;
    for (int i = 1; i <= n; i++)
        h[i] = i;
    for (int i = 1; i <= pos; i++)
    {
        int len = sides[i].len;
        int from = sides[i].from, to = sides[i].to;
        int ff = find(from), ft = find(to);
        if (ff == ft)
            continue;
        else
        {
            count++;
            h[ft] = ff;
            ans += len;
            if (count == n)
                break;
        }
    }
    return ans;
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        scanf("%d", &arr[i]);
    // 无向图的最大生成树
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
        {
            if (i != j)
            {
                int x = arr[i], y = arr[j];
                int len = ((ll)quick(x, y, m) + quick(y, x, m)) % m;
                sides[++pos] = {len, i, j};
            }
        }
    sort(sides + 1, sides + pos + 1);
    /*  for (int i = 1; i <= pos; i++)
     {
         cout << sides[i].len << " " << sides[i].from << " " << sides[i].to << endl;
     } */
    cout << Kruskal();
    return 0;
}

 《F - Union of Two Sets》

思维

 

 

 一道构造题，最先我被启发的是用线段树的方式来写：

想着N只有4000，那么我可以像线段树一样将[1,4000]不断分下去知道分到[1,1].....[4000,4000]

然后在分得的区间中找到两个区间可以使得满足[l1,r1]U[l2,r2]=[L,R]

但是我发现我错了：我天真地认为线段树的方法分的区间，对于任意给定一个区间来说都可以用两个分得的区间表示

但是这是错误的，因为比如：

我想求[2,4000],这个就不可能用线段树分的两个区间组成

因为线段树的分法：每次对数值一半分，这导致比如1与2要在十分深的地方才被分开，根本就没有连好的一整块

 

 

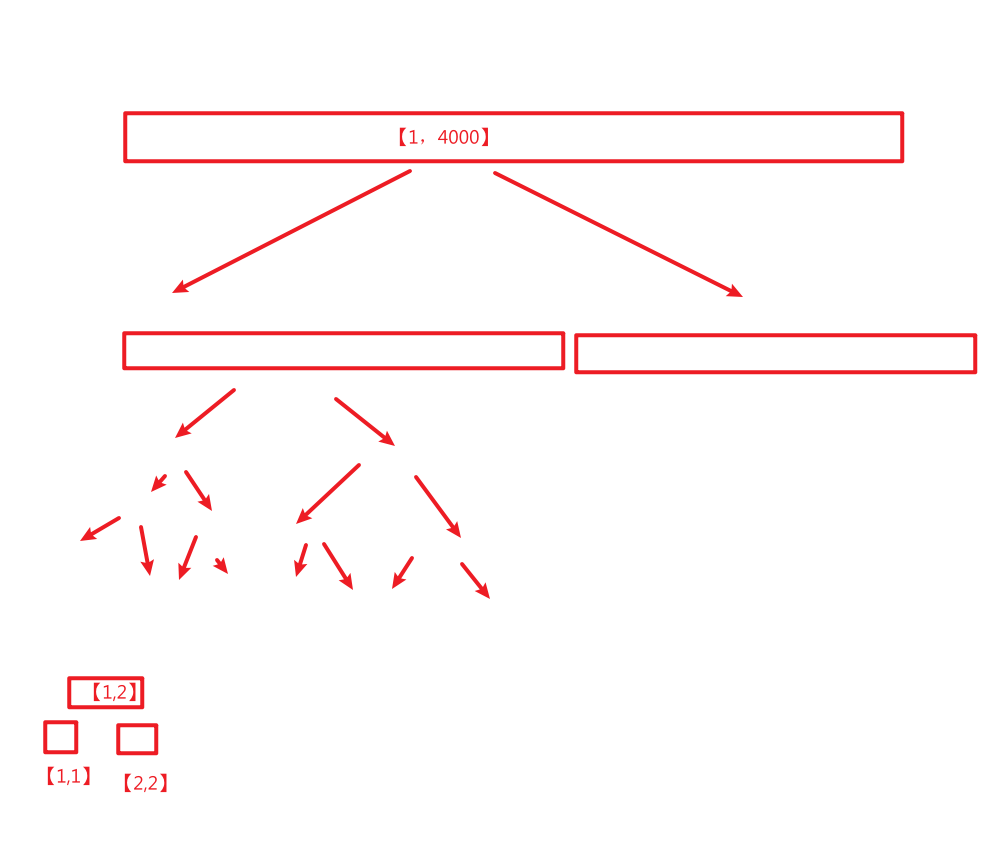
而且比如像 [1,2] [3,4] [5,6]..............

 

没有[2,3],[ 4,5]............

 

对于此，解决的方法是：因为N只有4000，给出[L,R],我们要用自己写的全部区间中的两个区间的和来组成[L,R]

 

 

 给定数len,其必定可以用两个属于1~loglen+1的 2的幂 组成

但是这道题是构造题那就将想法搞的更好写代码一点：

 

 

 

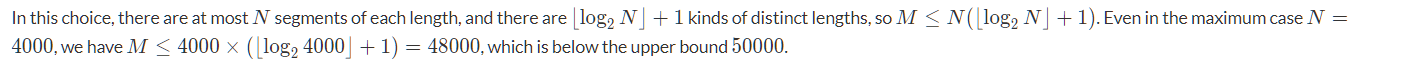
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
const int N = 4002;
struct node
{
    int l, r;
    int num;
} arr[N][N];
int pos[N];
int n, q, m = 0;
void find(int l, int r)
{
    int len = r - l + 1;
    int k = log2(len);
    int qlen = pow(2, k);
    int ansl, ansr;
    for (int i = 1; i <= pos[k]; i++)
    {
        if (arr[k][i].l == l)
        {
            ansl = arr[k][i].num;
            break;
        }
    }
    for (int i = 1; i <= pos[k]; i++)
    {
        if (arr[k][i].r == r)
        {
            ansr = arr[k][i].num;
            break;
        }
    }
    cout << ansl << " " << ansr << endl;
}
int main()
{
    memset(pos, 0, sizeof(pos));
    cin >> n;
    for (int i = 0; i <= log2(n) + 1; i++)
        for (int j = 1; j <= n; j++)
        {
            int len = pow(2, i);
            if (j + len - 1 <= n)
            {
                m++;
                arr[i][++pos[i]] = {j, j + len - 1, m};
            }
        }
    cout << m << endl;
    for (int i = 0; i <= log2(n) + 1; i++)
        for (int j = 1; j <= pos[i]; j++)
            cout << arr[i][j].l << " " << arr[i][j].r << endl;
    cin >> q;
    while (q--)
    {
        int l, r;
        scanf("%d%d", &l, &r);
        find(l, r);
    }
    return 0;
}