数论基础总集

大部分都是参考此博客：https://www.zhihu.com/column/c_1458888988497420288

《扩展欧几里得定理》

　　《欧几里得算法》

gcd(a,b)=gcd(b,a%b);

 

 

 《欧拉函数》

 

 

 

 

 

 

 

 

 《欧拉定理》

 

 

 《小费马定理》

 

 

 《卢卡斯定理》

 

 

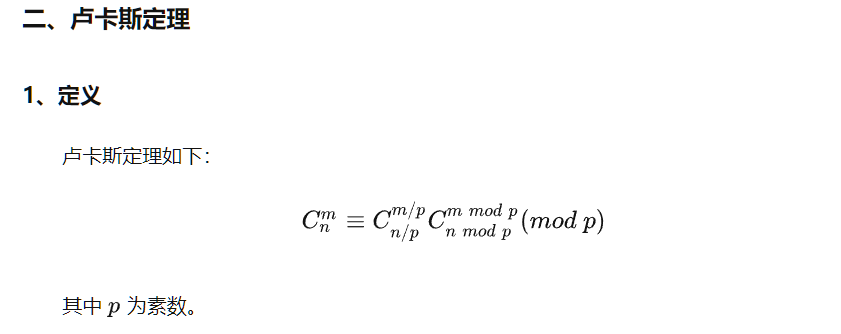
 《组合数》

 

 

 

 

 

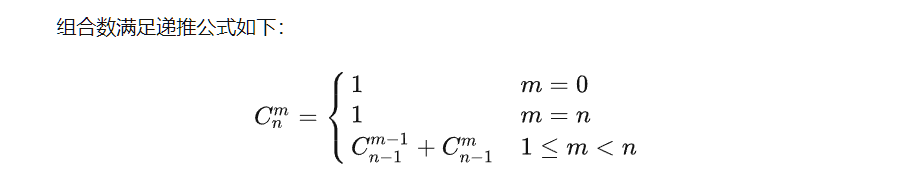
 上面的求组合数在模p下的值，为啥要用逆元？因为除法不好用逆元

这下面就扯到逆元了

《逆元》

 

 

 

 

 

 

 

 

 

 

 

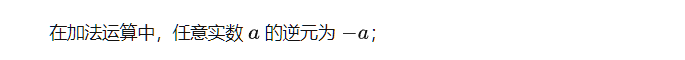
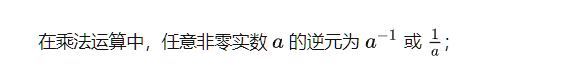
 如何求逆元？

由小费马定理，如果a与p互素，则a^(p-1)=1(modp)

则在这个条件下a的逆元其实就是a^(p-2);

如何求a^(p-2),在p比较大的情况下，而且还是在modp的情况下？

下面就涉及到了二分快速幂

《二分快速幂》

 

 

 最重要的还是下面的二进制优化法：

 

 

 

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
int qmi(int a, int b, int mod)
{
    //答案
    int res = 1;
    //乘数
    int mul = a;
    while (b)
    {
        //在二进制下b的第0位是否是1
        //是1则要乘,否则不要
        if (b & 1)
            res = res * 1LL * mul % mod;
        mul = mul * 1LL * mul % mod;
        b = b >> 1;
    }
    return res;
}
int main()
{
    int n;
    cin >> n;
    while (n--)
    {
        int a, b, mod;
        cin >> a >> b >> mod;
        cout << qmi(a, b, mod) << endl;
    }
    return 0;
}

 

《矩阵快速幂》

　　即求矩阵A的 A^k

　　与普通的快速幂相同，只是*的时候要按照矩阵的规则去求

　　即：

 

　　系列题目参照　

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
typedef long long ll;
const ll mod = 1e9 + 7;
ll n, k;
struct Matrix
{
    ll g[102][102];
} a;
Matrix operator*(const Matrix &x, const Matrix &y)
{
    Matrix t;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            t.g[i][j] = 0;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= n; k++)
                t.g[i][j] = (t.g[i][j] + (x.g[i][k] * y.g[k][j]) % mod) % mod;
    return t;
}
Matrix ans;
void quick()
{
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            ans.g[i][j] = (i == j ? 1 : 0);
    while (k)
    {
        if (k & 1)
            ans = ans * a;
        k >>= 1;
        a = a * a;
    }
}
int main()
{
    cin >> n >> k;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            cin >> a.g[i][j];
    quick();
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
            cout << ans.g[i][j] << " ";
        cout << endl;
    }
    return 0;
}

 运用：矩阵加速

 　　在求一些能够迭代的式子中，通常可以用矩阵的运算方式进行求解

　　　　如

　　　　

 

　　　　　这个就可以写成：

 

　　　　　　　我们知道这个可以迭代：fi=fi-1+fi-2

 

　　　　　　　但是当i十分大的时候如何办？ （如：i>=1e12）

 

　　　　　其实这个式子可以用矩阵的方式求解：

　　　　　　　　

 

 　　　　　　　　　　　　　

 

 

 

 

 

 

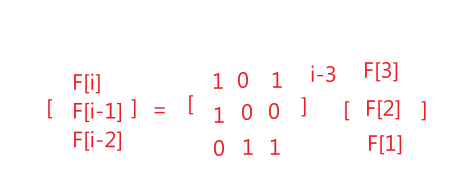
　　　　　再如：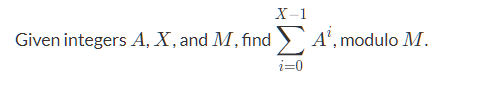

 

 　　　　　　　　　　

 

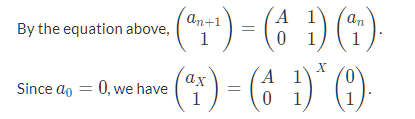
　　　　　　　　主要是进行构造

 

 

　　　　以第一个例子为例：

　　　　　　

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 4, mod = 1e9 + 7;
int n = 3;
struct Matrix
{
    ll g[N][N];
};
Matrix operator*(const Matrix &x, const Matrix &y)
{
    Matrix t;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            t.g[i][j] = 0;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= n; k++)
                t.g[i][j] = (t.g[i][j] + (x.g[i][k] * y.g[k][j]) % mod) % mod;
    return t;
}
ll p;
Matrix a;
void init()
{
    a.g[1][1] = 1, a.g[1][2] = 0, a.g[1][3] = 1;
    a.g[2][1] = 1, a.g[2][2] = 0, a.g[2][3] = 0;
    a.g[3][1] = 0, a.g[3][2] = 1, a.g[3][3] = 0;
}
void solve()
{
    init();
    cin >> p;
    p--;
    Matrix ans;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            ans.g[i][j] = (i == j ? 1 : 0);
    while (p)
    {
        if (p & 1)
            ans = ans * a;
        p >>= 1;
        a = a * a;
    }
    ll t[][2] = {
        {0, 0},
        {0, 1},
        {0, 1},
        {0, 1}};
    ll res[4][4];
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            res[i][j] = 0;
    for (int i = 1; i <= 3; i++)
        for (int k = 1; k <= 3; k++)
            res[i][1] = (res[i][1] + (ans.g[i][k] * t[k][1]) % mod) % mod;
    cout << res[3][1] << endl;
}
int main()
{
    int t;
    cin >> t;
    while (t--)
        solve();
    return 0;
}

 

 

 

 

 

 

---