dp----状态压缩dp

《基于连通性的棋盘式状态压缩dp》

因为最典型的例子是放棋盘的一类问题所以我们叫他为棋盘式：典型例子如下：https://www.acwing.com/problem/content/1066/

 

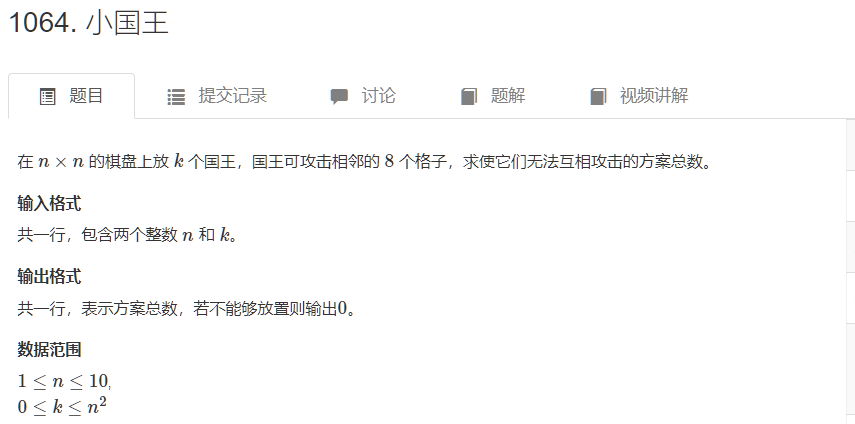
 像这类题目如果以dfs的方式思考是不好想的，不如从上到下枚举一下到底每一行的状态到底是如何的，

因为由题目可知：第i行的棋子摆放方式与第i-2行无关，仅仅与第i-1行和第i行相邻的有关。

所以我们可以将每一行放棋子的地方看做为1，不放的地方为0，于是就有了一行的状态可以以二进制的状态表示

因为最大的状态为2^n(n为行数),本题中也就为1024（10进制下）

所以我们完全可以枚举每一行的状态，然后再由上面的状态转移过来：

 

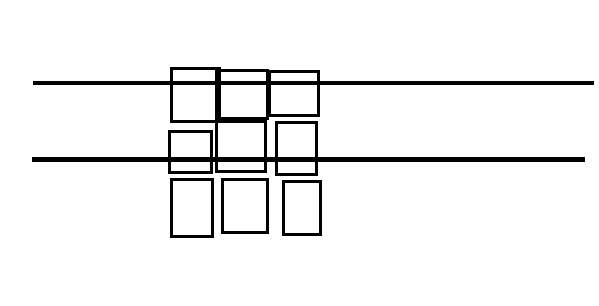
 我们这里的棋子模型是8面的，所以在不同的两行（假设这一行为a,上一行为b）

1.同一行上放棋子不能相邻(用代码表示：(state & (state>>1))==0 , 相当于二进制下右移了，

　　　　因为规定1旁必定是0，出现(state & (state>>1))!=0,说明不符合规定了)

2.a，b两行放棋子不能在同一列上（用代码表示： (stateA & stateB)==0,符合不在同一列上），

　　不能在相邻列上（用代码表示： state=(stateA | stateB),然后判断state是否有相邻的1（用上面的1方法即可）） 

通过上面的两个条件的筛选我们就可以除去大部分状态，然后dp即可：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
const int N = 11;
// dp[i][j][k]的含义是在1~i层,第i层状态为j时,总共用了k个国王而且这些国王不相互攻击的方案数；
int n, g;
long long dp[N][2 << N][N * N];

// 在我以前的小国王设计中我感受到了明显的设计问题：
//  1.在for循环中去判断两个状态是否合法，而不是把他封装成函数
//  2.其实两个状态是否合法的判断我也写的不是很好:在判断两个状态是否可以在一起，只要求|，然后判断其是否有相邻的1即可
//  3.不仅仅是一行上合法状态我们可以预处理出来,而且两个状态是否可以在一起我们可以预处理出来

// rstate[]是保存状态相邻无1的合法状态
int rstate[2 << N], icnt = 0, oneNum[2 << N];
vector<int> mapstate[2 << N];
// check()是判断枚举的状态x是否有相邻的1
bool check(int x)
{
    return !(x & (x >> 1));
}
// 判断上下两行状态是否满足相应条件
int legal(int a, int b)
{
    if ((a & b) == 0 && check(a | b))
        return true;
    else
        return false;
}
int count(int x)
{
    int res = 0;
    for (int i = 0; i < n; i++)
        if ((x >> i) & 1 == 1)
            res++;
    return res;
}
int main()
{
    cin >> n >> g;
    for (int i = 0; i < (1 << n); i++)
        if (check(i))
        {
            rstate[icnt++] = i;
            oneNum[i] = count(i);
        }
    for (int i = 0; i < icnt; i++)
        for (int j = 0; j < icnt; j++)
            if (legal(rstate[i], rstate[j]))
                mapstate[i].push_back(rstate[j]);
    
    //注意这里:
    dp[0][0][0] = 1;
    for (int i = 1; i <= n; i++)
        for (int j = 0; j < icnt; j++)
        {
            int nstate = rstate[j];
            for (int u = 0; u < mapstate[j].size(); u++)
            {
                int pstate = mapstate[j][u];
                for (int k = 0; k <= g; k++)
                    if (k >= oneNum[nstate])
                        dp[i][nstate][k] += dp[i - 1][pstate][k - oneNum[nstate]];
            }
        }

    long long res = 0;
    for (int i = 0; i < icnt; i++)
    {
        res += dp[n][rstate[i]][g];
    }
    cout << res;
    return 0;
}

再如这个题：https://www.acwing.com/problem/content/329/

 

 

 

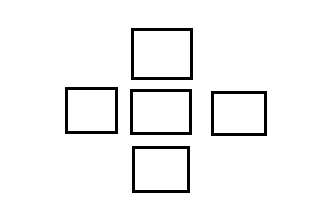
 与上面不同的是这个棋子是4面的，而且除了有些土地不能用之外，其他条件与上面都相同。

分析方式也一样：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
const int N = 14, MOD = 1e8;
// dp[i][j]:表示在前1~i-1行中种完了玉米，然后第i行的状态为j的方案数
int dp[N][1 << N], g[N], m, n;
// 这里是保存一行中合法的状态
vector<int> rstate;
vector<int> mapstate[1 << N];
int main()
{
    cin >> m >> n;
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
        {
            int t;
            scanf("%d", &t);
            g[i] += (!t) << (j - 1);
        }

    for (int i = 0; i < 1 << n; i++)
        if (!(i & (i >> 1)))
            rstate.push_back(i);

    // 表示在i状态下可以在其上面的j状态
    for (int i = 0; i < rstate.size(); i++)
        for (int j = 0; j < rstate.size(); j++)
            if (!(rstate[i] & rstate[j]))
                mapstate[i].push_back(j);

    dp[0][0] = 1;
    for (int i = 1; i <= m; i++)
        for (int a = 0; a < rstate.size(); a++)
        {
            int nowstate = rstate[a];
            if (!(nowstate & g[i]))
                for (int b = 0; b < mapstate[a].size(); b++)
                {
                    int prestate = rstate[mapstate[a][b]];
                    dp[i][nowstate] = (dp[i][nowstate] + dp[i - 1][prestate]) % MOD;
                }
        }

    int ans = 0;
    for (int i = 0; i < rstate.size(); i++)
        ans = (ans + dp[m][rstate[i]]) % MOD;
    cout << ans;
    return 0;
}

《集合式状态压缩dp》

愤怒的小鸟

 

 

 

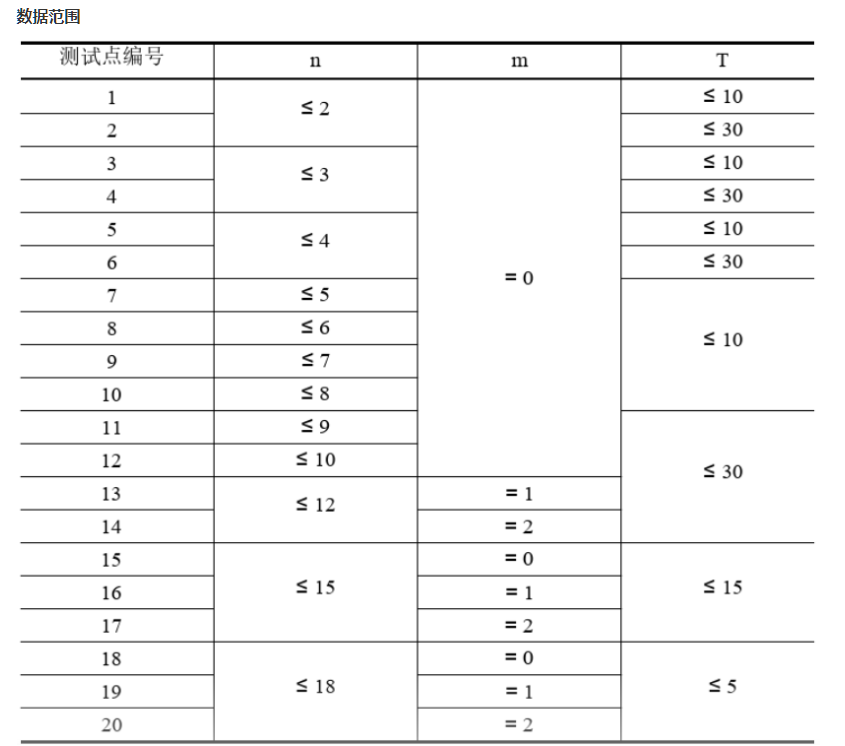
 看一下n很小，可以通过两个点确定一条抛物线：注意这条这条抛物线的a<0

我们用全部确定的抛物线看一下那些点在这个上面

然后这个问题变成了：我们要选那些抛物线才可以将猪猪全部覆盖（打下来），要求抛物线选的尽可能少

这个问题其实有个学名：“重复点覆盖问题”，这里我们就不去考虑这个问题

从dfs角度上可以怎么作？

我们可以将每一个猪猪看出01，如果其中一个猪猪被打下来了，那么我们将其计为1，否则为0

于是对于n个猪猪，可以用二进制代表，全部猪猪的状态

这个就是用状态压缩表示集合

写dfs的话为：dfs(state,cnt); 表示我用了cnt个抛物线（鸟），到达了state的状态

当state==(1<<n)-1的时候就 ans=min(ans,cnt)

状态的转移为dfs(state| 这条抛物线能够打到的猪猪，cnt+1);

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
using namespace std;
typedef pair<double, double> PDD;
#define x first
#define y second
const int N = 20;
// 步骤：
// 1.首先需要根据两点求出全部可能的抛物线,然后确定每一条抛物线上的能够覆盖的点
// 2.然后用dfs解决重复覆盖问题;
int ans, n, m, t;
// path[i][j]用来表示过点i和点j的抛物线能过的点集
int path[N][N], dp[1 << N];
PDD pigs[N];
// dfs(state,cnt):表示当到达状态state时用了cnt个抛物线(鸟)
/* void dfs(int state, int cnt)
{
    if (state == ((1 << n) - 1))
        ans = min(ans, cnt);
    int node;
    // 先任选还没有被覆盖的点
    for (int i = 1; i <= n; i++)
        if ((state >> (i - 1))&1 == 0)
        {
            node = i;
            break;
        }
    // 然后再枚举能够通往这个点的全部抛物线
    for (int i = 1; i <= n; i++)
        dfs(node | path[node][i], cnt + 1);
} */

但是dfs会超时，我们把dfs转换为for循环，用dp数组记录已经算到到达state状态的最小抛物线数

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
using namespace std;
typedef pair<double, double> PDD;
#define x first
#define y second
const int N = 20;
// 步骤：
// 1.首先需要根据两点求出全部可能的抛物线,然后确定每一条抛物线上的能够覆盖的点
// 2.然后用dfs解决重复覆盖问题;
int ans, n, m, t;
// path[i][j]用来表示过点i和点j的抛物线能过的点集
int path[N][N], dp[1 << N];
PDD pigs[N];
// dfs(state,cnt):表示当到达状态state时用了cnt个抛物线(鸟)
/* void dfs(int state, int cnt)
{
    if (state == ((1 << n) - 1))
        ans = min(ans, cnt);
    int node;
    // 先任选还没有被覆盖的点
    for (int i = 1; i <= n; i++)
        if ((state >> (i - 1))&1 == 0)
        {
            node = i;
            break;
        }
    // 然后再枚举能够通往这个点的全部抛物线
    for(int i=1;i<=n;i++)
        dfs(state|path[node][i],cnt+1);
} */
int main()
{
    cin >> t;
    while (t--)
    {
        memset(path, 0, sizeof(path));
        cin >> n >> m;
        for (int i = 1; i <= n; i++)
            scanf("%lf %lf", &pigs[i].x, &pigs[i].y);
        for (int i = 1; i <= n; i++)
        {
            // 表示只过点i的抛物线
            // 这里是解决当n==1时的边界情况
            path[i][i] = 1 << (i - 1);
            for (int j = 1; j <= n; j++)
            {
                double x1 = pigs[i].x, y1 = pigs[i].y;
                double x2 = pigs[j].x, y2 = pigs[j].y;
                if (fabs(x1 - x2) < 1e-8)
                    continue;
                double a = (y1 / x1 - y2 / x2) / (x1 - x2);
                double b = y1 / x1 - a * x1;
                // 万分注意这里:一定要a<0才行
                if (fabs(a - 0) < 1e-8 || a > 0)
                    continue;
                int state = 0;
                for (int k = 1; k <= n; k++)
                {
                    double x3 = pigs[k].x;
                    double y3 = a * x3 * x3 + b * x3;
                    // 说明点k在这条抛物线上:
                    if (fabs(y3 - pigs[k].y) < 1e-8)
                        state += 1 << (k - 1);
                }
                path[i][j] = state;
            }
        }
        memset(dp, 0x3f, sizeof(dp));
        dp[0] = 0;
        // 因为我们这里是根据dfs改成的for循环,在dfs中当state==1<<n-1时就该返回了
        // 这里我们也一样，所以状态i不用枚举到1<<n-1;
        for (int i = 0; i < (1 << n) - 1; i++)
        {
            int node;
            for (int j = 1; j <= n; j++)
            {
                if (!((i >> (j - 1)) & 1))
                {
                    node = j;
                    break;
                }
            }
            // 从初状态i到达新状态用了path[node][j]这条抛物线
            for (int j = 1; j <= n; j++)
                dp[i | path[node][j]] = min(dp[i | path[node][j]], dp[i] + 1);
        }
        if (m == 1)
            ans = (n % 3 == 0) ? n / 3 + 1 : n / 3 + 2;
        else
            ans = n;
        ans = min(ans, dp[(1 << n) - 1]);
        cout << ans << endl;
    }
    return 0;
}