第十二届蓝桥杯c++B组
《货物摆放》
思维,约数
很明显,L,W,H都是n的约数,我们只要求一下n的约数,然后三重循环枚举其每一个约数看一下是否能L*W*H=n
有可能你会担心n的约数特别多,但是自己写个程序跑一下就知道十分少
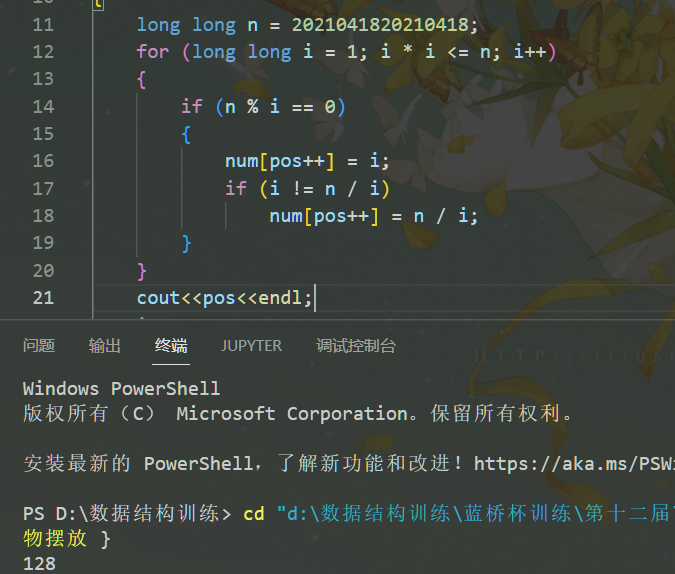
才128个三重循环绝对不会超时,其实也可以优化到二重循环
1 #include <iostream>
2 #include <algorithm>
3 #include <cstring>
4 #include <cmath>
5 using namespace std;
6 const int N = 1e7;
7 long long num[N];
8 int pos = 0;
9 int main()
10 {
11 long long n = 2021041820210418;
12 for (long long i = 1; i * i <= n; i++)
13 {
14 if (n % i == 0)
15 {
16 num[pos++] = i;
17 if (i != n / i)
18 num[pos++] = n / i;
19 }
20 }
21 /* cout<<pos<<endl; */
22 int ans = 0;
23 for (int i = 0; i < pos; i++)
24 for (int j = 0; j < pos; j++)
25 for (int k = 0; k < pos; k++)
26 if (num[i] * num[j] * num[k] == n)
27 ans++;
28 cout << ans;
29 return 0;
30 }
《砝码称重》
dp
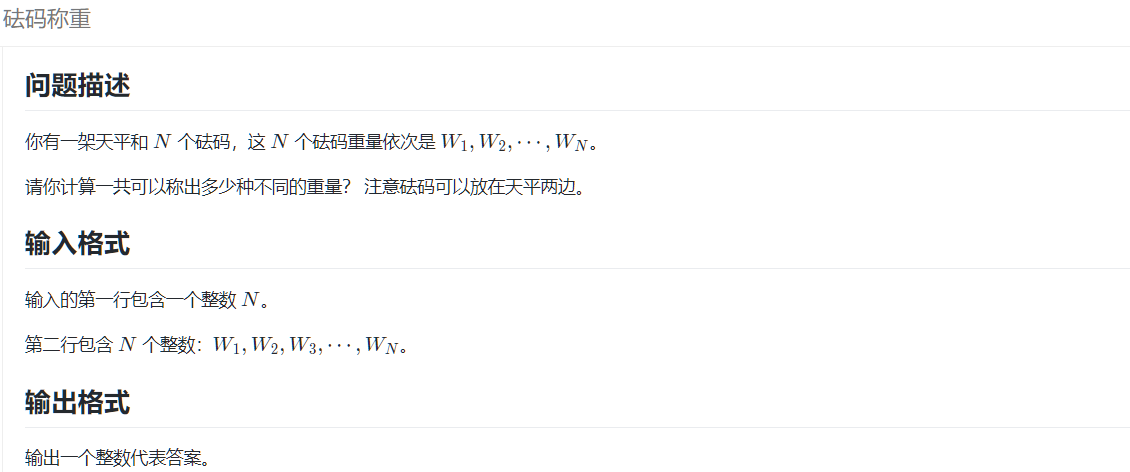
dp[i][j]:表示从前i个砝码中选,能否称出重量j;
有如下三种转移方式:
dp[i][j]<-----------dp[i-1][j]
dp[i][j]<-----------dp[i-1][j+w[i]]
dp[i][j]<-----------dp[i-1][abs(j-w[i])]
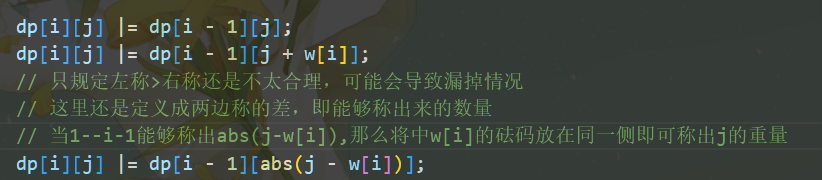
一开始我的想法是:规定左称一定>右称
然后转移方式成了:这个转移方式总会漏掉方案
1 #include <iostream>
2 #include <algorithm>
3 #include <cstring>
4 using namespace std;
5 const int N = 105, M = 100005;
6 int dp[N][M], w[N];
7 int main()
8 {
9 int allw = 0, ans = 0, n;
10 cin >> n;
11 for (int i = 1; i <= n; i++)
12 {
13 scanf("%d", &w[i]);
14 allw += w[i];
15 }
16 dp[0][0] = 1;
17 for (int i = 1; i <= n; i++)
18 for (int j = 0; j <= allw; j++)
19 {
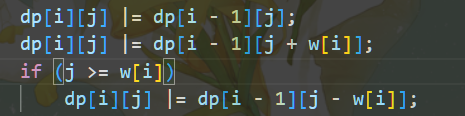
20 dp[i][j] |= dp[i - 1][j];
21 dp[i][j] |= dp[i - 1][j + w[i]];
22 // 只规定左称>右称还是不太合理,可能会导致漏掉情况
23 // 这里还是定义成两边称的差,即能够称出来的数量
24 // 当1--i-1能够称出abs(j-w[i]),那么将中w[i]的砝码放在同一侧即可称出j的重量
25 dp[i][j] |= dp[i - 1][abs(j - w[i])];
26 }
27 for (int i = 1; i <= allw; i++)
28 if (dp[n][i])
29 ans++;
30 cout << ans;
31 return 0;
32 }
《直线》
思维

这道题开始我的思路是没问题的,就是四重for循环枚举两点,然后通过y=kx+d,这种直线的形式计算是否是同一种直线
但是我就错在用map<pair<double,double>,bool>vis;来判断这条直线我是否以前看过;但是对于double是不能够用map来判断的
因为double在计算的时候有精度误差问题:比如10/3,用计算机如果计算多次然后用==来判断其是否相等是错误的
应该用这两个的差的绝对值是否<1e-8来判断
对于这个问题我们应该先将算到的直线保存,然后排序,然后比较其是否是相等的
1 #include <iostream>
2 #include <algorithm>
3 #include <cstring>
4 #include <cmath>
5 using namespace std;
6 const int N = 1e6;
7 struct node
8 {
9 double k, d;
10 bool operator<(const node &t) const
11 {
12 if (k == t.k)
13 return d < t.d;
14 else
15 return k < t.k;
16 }
17 } line[N];
18 int n = 0, ans = 0;
19 int main()
20 {
21 int ans = 41;
22 for (int y1 = 0; y1 < 21; y1++)
23 for (int x1 = 0; x1 < 20; x1++)
24 for (int y2 = 0; y2 < 21; y2++)
25 for (int x2 = 0; x2 < 20; x2++)
26 {
27 if (y1 != y2 && x1 != x2)
28 {
29 double k = double(y1 - y2) / double(x1 - x2);
30 double d = y1 - k * x1;
31 line[n++] = {k, d};
32 }
33 }
34 sort(line, line + n);
35 for (int i = 0; i < n - 1; i++)
36 {
37 if (fabs(line[i].k - line[i + 1].k) > 1e-8 || fabs(line[i].d - line[i + 1].d) > 1e-8)
38 ans++;
39 }
40 ans++;
41 cout << ans;
42 return 0;
43 }
《杨辉三角》
数学,思维

首先要明白一个数学问题:对于杨辉三角上的每一个数都可以用C(i,j)表示
i是杨辉三角上每一行上的第i列(从0开始数),j是杨辉三角上的行(从0开始数)
比如 5就可以表示为C(1,5);

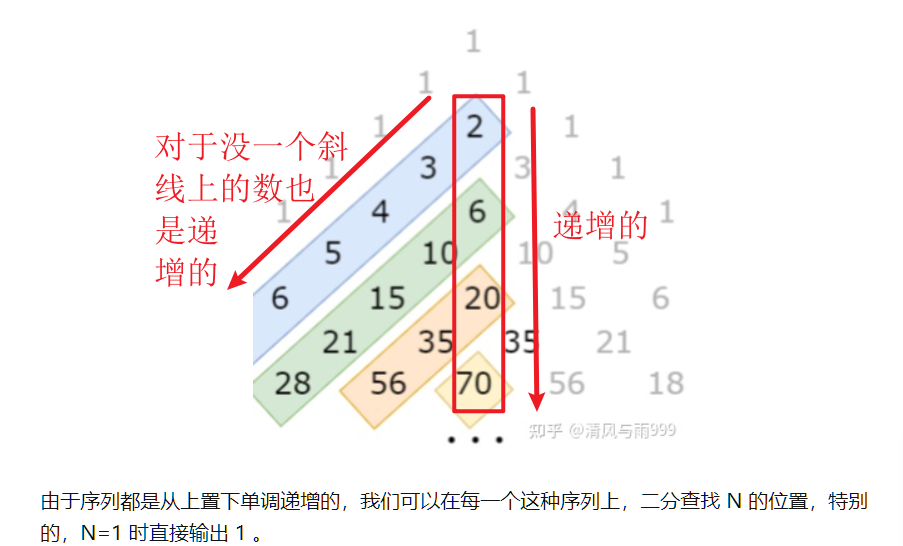
而且这中间一束上的 数可以表示为 C(0,0),C(1,2),C(2,4),C(3,6)................可以看到十分有规律
即C(t,2*t),而且C(15,30)>1e9,我们可以先二分这一束数,得到一个行号,代表num一定就在0-t行为开头的斜线上
再对每一个斜线二分
注意写C(i,j)时的巧妙之处
1 #include <iostream>
2 #include <algorithm>
3 #include <cstring>
4 using namespace std;
5 int num;
6 long long C(int a, int b)
7 {
8 long long res = 1;
9 //这里一定不能写成for(int i=b,j=a;j>=1;j--)
10 //因为如果像上面这样写C(3,7)这样的会因为除出来忽略小数而错误
11 for (int i = b, j = 1; j <= a; i--, j++)
12 {
13 res = res * i / j;
14 // 这一条语句十分有用,因为如果当求C(i,j)时,如果>num,就求的没有意义了;
15 // 而且这样可以避免数据过大溺出的情况;
16 if (res > num)
17 return res;
18 }
19 return res;
20 }
21 long long getSum(int i, int j)
22 {
23 return (long long)(1 + j) * (long long)j / 2 + i + 1;
24 }
25 int main()
26 {
27 // 现在列中找到最大的小于数num的C(a,2a);
28 // 然后对于其C(a,2a+i),这一斜线上找到是否有数num.
29 // 如果没有a--,继续在斜线上找;
30 // 如果有我们可以通过C(i,j)知道其在第j+1行,第i+1列
31 // sum=(1+...+j+i)=(1+j)*j/2+i;
32
33 cin >> num;
34 // 因为C(15,30)>1e9所以我们从0-15;
35 int l = 0, r = 15, t;
36 while (l <= r)
37 {
38 int mid = l + r >> 1;
39 if (C(mid, 2 * mid) > num)
40 r = mid - 1;
41 else
42 {
43 t = mid;
44 l = mid + 1;
45 }
46 }
47 /* cout << t << endl; */
48 if (C(t, 2 * t) == num)
49 cout << getSum(t, 2 * t);
50 else
51 {
52 // 开始从斜线上查找:
53 int l, r, tt;
54 while (t)
55 {
56 l = 2 * t, r = 1e9, tt;
57 while (l <= r)
58 {
59 int mid = l + r >> 1;
60 if (C(t, mid) > num)
61 r = mid - 1;
62 else
63 {
64 tt = mid;
65 l = mid + 1;
66 }
67 }
68 /* cout << "!" << t << " " << tt << " " << C(t, tt) << endl; */
69 if (C(t, tt) == num)
70 break;
71 else
72 t--;
73 }
74 cout << getSum(t, tt);
75 }
76 return 0;
77 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号