图论----欧拉路径与欧拉回路
好博客:
https://www.acwing.com/solution/content/53434/
https://ycw123.blog.luogu.org/ou-la-hui-lu-yu-ou-la-lu-jing
《介绍与性质》


对于无向图来说:
如果不是欧拉回路:
起点的度是奇数(度是出度+入度),因为我们从起点出发,如果以后还到达了起点,必然是进入起点,
然后离开起点(因为我这里的前提是:不是欧拉回路,是欧拉路径)。所以度是奇数
同理,终点的度也是奇数
其余的中间点度都是偶数
如果是欧拉回路:
从起点出发,到起点结束,全部节点的度都是偶数
对于有向图来说:
如果不是欧拉回路:
起点的出度=起点的入度+1,终点的入度=终点的出度+1
其余点出度==入度
如果是欧拉回路:
全部点:出度==入度
《关于建立图上的注意点》
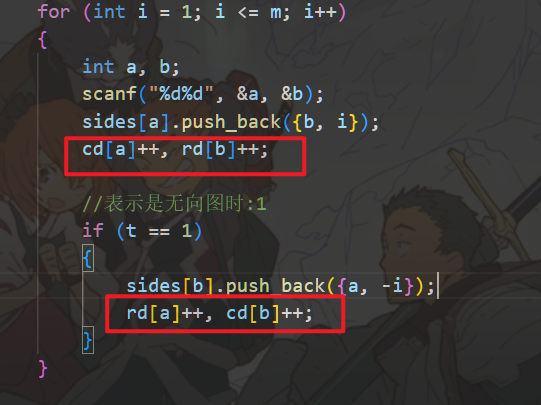
在判断是否可以建成欧拉回路或欧拉路径的过程中我们会用上cd[].rd[],表示一个点的出度与入度
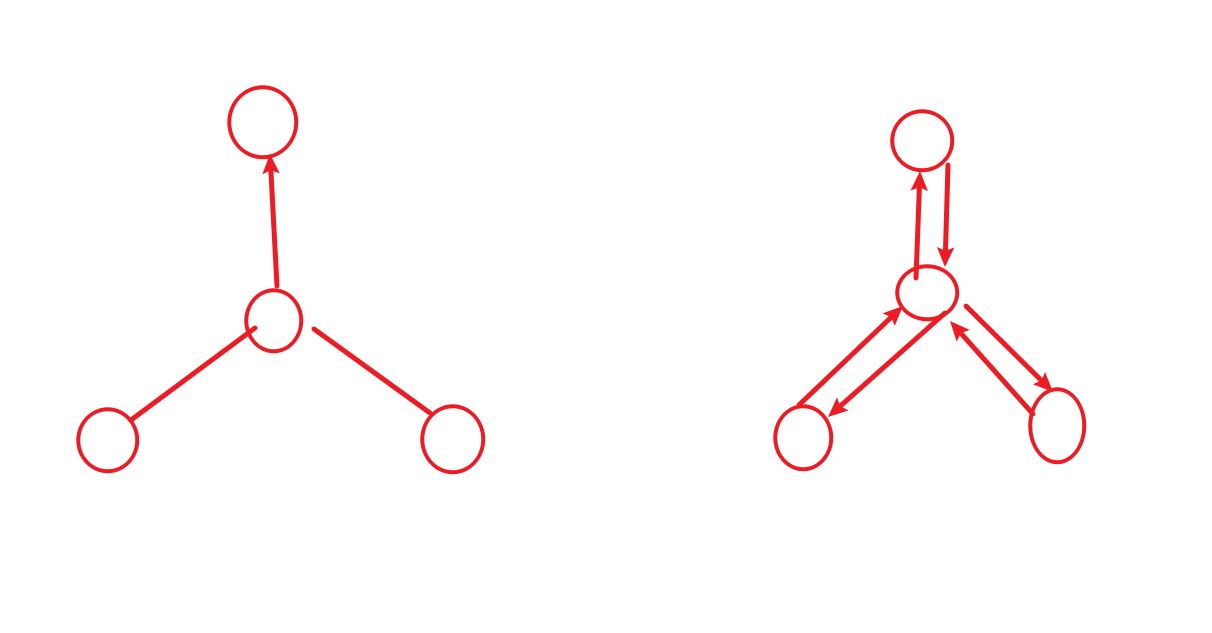
在无向图的建立过程中,我一般习惯如下:
这个时候我其实把无向图建立成了上面右边的情况
但是其实当边a->b用过后,b->a边也应该判断为用过
这个时候我判读是否可以有欧拉回路的条件是:

像这个图也可以建成欧拉回路,所以不能单独只通过bool vis,这种来判断边是否被看过,特别是在无向图的建边过程中
因为有多个自环与重边在欧拉路径中是被允许的
《一些问题》
如何记录欧拉路径?
如何在使用vector建边时删去边?
原题:https://www.acwing.com/problem/content/1186/
1 #include <iostream>
2 #include <algorithm>
3 #include <cstring>
4 #include <vector>
5 #include <map>
6 #include <stack>
7 using namespace std;
8 const int N = 1e5 + 5;
9 int t, n, m, rd[N], cd[N];
10 struct node
11 {
12 int to, w;
13 };
14 //在使用结构体map的时候一定要用operator重载一下,否则会报错
15 struct Node
16 {
17 int from, to, w;
18 bool operator<(const Node &a) const
19 {
20 if (a.from == from)
21 {
22 if (a.to == to)
23 return a.w < w;
24 else
25 return a.to < to;
26 }
27 else
28 return a.from < from;
29 }
30 };
31 stack<int> ans;
32 vector<node> sides[N];
33 map<Node, bool> vis;
34 //用来模拟删除边的数组,pos[i]表示在sides[i]中下次要看的边是
35 // sides[i][pos[i]],0~pos[i]-1的边都已经看过;
36 int pos[N];
37
38 void dfs(int x)
39 {
40 //这里后面更新是i=max(i+1,pos[x]),而不是i=pos[x]
41 //是因为可能里面的if语句进不去,防止导致死循环
42 for (int i = pos[x]; i < sides[x].size(); i = max(i + 1, pos[x]))
43 {
44 int to = sides[x][i].to, w = sides[x][i].w;
45 if (!vis[{x, to, w}])
46 {
47 vis[{x, to, w}] = true;
48 if (t == 1)
49 vis[{to, x, -w}] = true;
50 pos[x] = i + 1;
51 dfs(sides[x][i].to);
52 //这是加入边的写法
53 ans.push(w);
54 }
55 //这个加入点的写法
56 // ans.push(x);
57 }
58 }
59 int main()
60 {
61 cin >> t >> n >> m;
62 for (int i = 1; i <= m; i++)
63 {
64 int a, b;
65 scanf("%d%d", &a, &b);
66 sides[a].push_back({b, i});
67 cd[a]++, rd[b]++;
68
69 //表示是无向图时:1
70 if (t == 1)
71 {
72 sides[b].push_back({a, -i});
73 rd[a]++, cd[b]++;
74 }
75 }
76
77 bool flag = true;
78 for (int i = 1; i <= n; i++)
79 if ((t == 1 && cd[i] % 2) || (t != 1 && cd[i] != rd[i]))
80 {
81 flag = false;
82 break;
83 }
84 if (flag)
85 {
86 for (int i = 1; i <= n; i++)
87 if (sides[i].size() != 0)
88 {
89 dfs(i);
90 break;
91 }
92
93 if (ans.size() != m)
94 cout << "NO" << endl;
95 else
96 {
97 cout << "YES" << endl;
98 while (ans.size())
99 {
100 cout << ans.top() << " ";
101 ans.pop();
102 }
103 cout << endl;
104 }
105 }
106 else
107 cout << "NO" << endl;
108 return 0;
109 }
无向图模板:
原题链接:https://www.luogu.com.cn/problem/P2731
这里用times[a][b]来记录边a->b的条数,上面不这么用是因为上面的点数太大,开二维会爆,所以以后能开二维就开二维吧,比较容易
1 #include <iostream>
2 #include <algorithm>
3 #include <cstring>
4 #include <map>
5 #include <vector>
6 #include <stack>
7 using namespace std;
8
9 typedef pair<int, int> PII;
10 const int N = 510;
11 vector<int> sides[N];
12 int times[N][N];
13
14 int m, cd[N], rd[N];
15 stack<int> ans;
16
17 int pos[N];
18 void dfs(int x)
19 {
20 for (int i = pos[x]; i < sides[x].size(); i = max(i + 1, pos[x]))
21 {
22 int to = sides[x][i];
23 if (times[x][to] > 0)
24 {
25 times[x][to]--, times[to][x]--;
26 pos[x] = i + 1;
27 dfs(to);
28 }
29 }
30 ans.push(x);
31 }
32
33 int main()
34 {
35 cin >> m;
36 int mind = 520, maxd = -520;
37 for (int i = 1; i <= m; i++)
38 {
39 int a, b;
40 scanf("%d%d", &a, &b);
41 mind = min(mind, min(a, b));
42 maxd = max(maxd, max(a, b));
43 sides[a].push_back(b);
44 sides[b].push_back(a);
45 cd[a]++, rd[b]++;
46 cd[b]++, rd[a]++;
47 times[a][b]++, times[b][a]++;
48 }
49 int start = -1;
50 for (int i = mind; i <= maxd; i++)
51 {
52 if (sides[i].size() != 0 && start == -1)
53 start = i;
54 if (sides[i].size() != 0 && cd[i] % 2)
55 {
56 start = i;
57 break;
58 }
59 }
60 for (int i = mind; i <= maxd; i++)
61 sort(sides[i].begin(), sides[i].end());
62
63 dfs(start);
64
65 while (ans.size())
66 {
67 cout << ans.top() << endl;
68 ans.pop();
69 }
70
71 return 0;
72 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号