区间问题----差分+离散化+前缀和

 

《二维离散化+二维前缀和+二维双指针算法+二分+以点代二维区间》

思路：

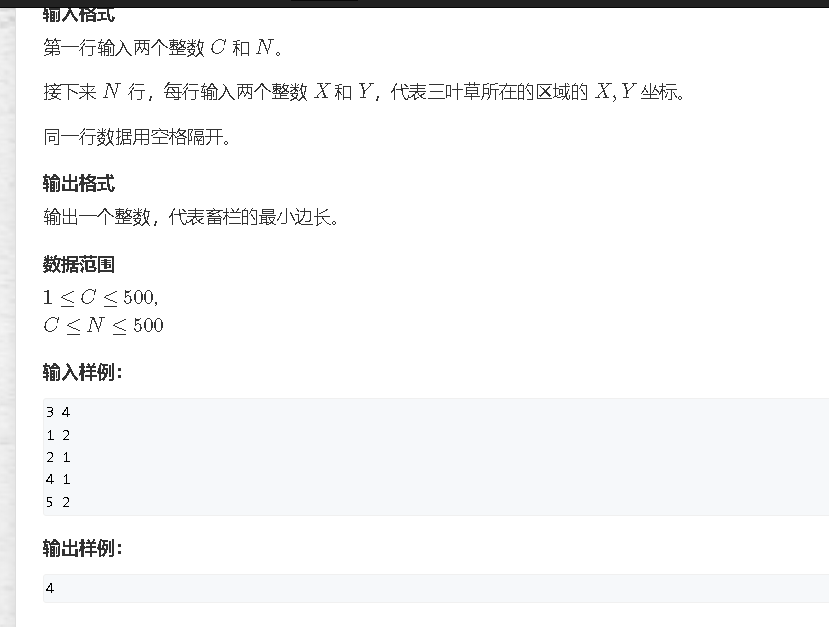
　　首先，利用二分，将求解问题变成判断问题，二分边长

　　关于在二维平面上的任意区域的数值问题可以用预处理二维前缀和解决

　　然后因为利用二分出来的边长，我们枚举在二维平面上的两个点，然后在通过前缀和算出这个区域上的草的数量，如果满足条件，return true;

 但是如果这里不离散化是做不了的，因为按照，枚举x与y要1e8时间复杂度，

但是这里N很小，x与y最多也只会出现1000次

1000*1000=1e6复杂度可以接受

#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 1010;
int c, n;
PII points[N];
vector<int> numbers;
int sum[N][N];
int get(int x)
{
    int l = 1, r = numbers.size() - 1, ans = -1;
    while (l <= r)
    {
        int mid = (l + r) >> 1;
        if (numbers[mid] >= x)
        {
            ans = mid;
            r = mid - 1;
        }
        else
            l = mid + 1;
    }
    return ans;
}
bool check(int len)
{
　　　　//可以发现我这里双指针，我只枚举了x2，y2的值，而x1与y1我并没有枚举，而是受了x2与y2的限制而移动
    for (int x1 = 1, x2 = 1; x2 < numbers.size(); x2++)
    {
        while (numbers[x2] - numbers[x1] + 1 > len)
            x1++;
        for (int y1 = 1, y2 = 1; y2 < numbers.size(); y2++)
        {
            while (numbers[y2] - numbers[y1] + 1 > len)
                y1++;
            if (sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1] >= c)
                return true;
        }
    }
    return false;
}
int main()
{
    cin >> c >> n;
    for (int i = 1; i <= n; i++)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        points[i] = {x, y};
        numbers.push_back(x), numbers.push_back(y);
    }
    numbers.push_back(0);
    sort(numbers.begin(), numbers.end());
    numbers.erase(unique(numbers.begin(), numbers.end()), numbers.end());

    /* for (int i = 0; i < numbers.size(); i++)
        cout << numbers[i] << " ";
    cout << endl; */

    for (int i = 1; i <= n; i++)
    {
        int x = get(points[i].first), y = get(points[i].second);
        /*   cout << "pos:" << x << " " << y << endl; */
        sum[x][y]++;
    }
    for (int i = 1; i < numbers.size(); i++)
        for (int j = 1; j < numbers.size(); j++)
            sum[i][j] += sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];
    int l = 1, r = 10000, ans = -1;
    while (l <= r)
    {
        int mid = (l + r) >> 1;
        if (check(mid))
        {
            ans = mid;
            r = mid - 1;
        }
        else
            l = mid + 1;
    }
    cout << ans;
    return 0;
}

《一维差分+一维以点代区间问题》

 

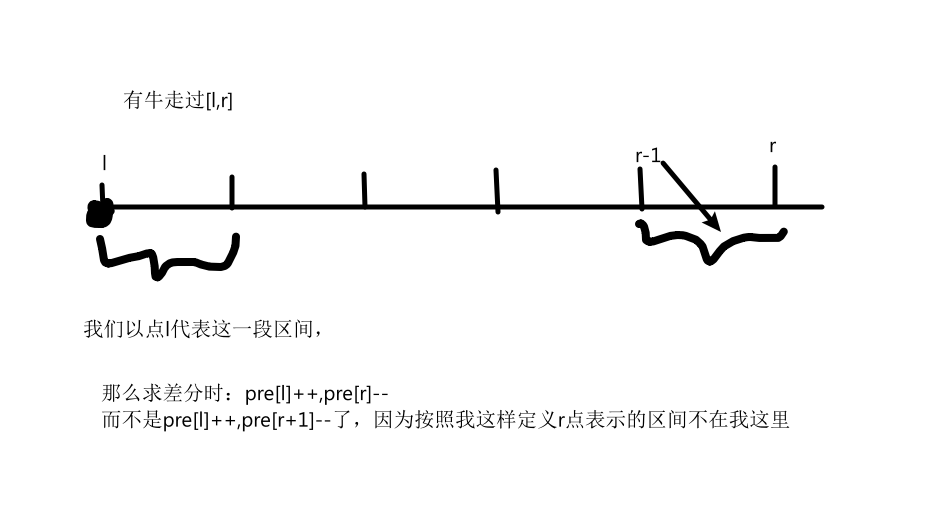
 思路：这道题是明显的离散化+差分，但是这里有个坑点：一维以点代区间

像这样的要定义好点的含义，否则会影响求前缀和与差分的规则

 

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 2 * 1e5 + 5, INF = 1e9 + 10;
int pre[N], n, sum[N];
vector<int> dist;
PII arr[N];
int get(int x)
{
    int l = 0, r = dist.size() - 1, ans;
    while (l <= r)
    {
        int mid = (l + r) >> 1;
        if (dist[mid] >= x)
        {
            ans = mid;
            r = mid - 1;
        }
        else
            l = mid + 1;
    }
    return ans;
}
int main()
{
    cin >> n;
    int pos = 0, nowpos;
    dist.push_back(0);
    dist.push_back(INF);
    dist.push_back(-INF);
    for (int i = 1; i <= n; i++)
    {
        int num;
        char c[2];
        scanf("%d", &num);
        scanf("%s", c);
        if (c[0] == 'R')
        {

            nowpos = pos + num;
            arr[i] = {pos, nowpos};
            /*   cout << pos << " " << nowpos << endl; */
        }
        else if (c[0] == 'L')
        {

            nowpos = pos - num;
            arr[i] = {nowpos, pos};
            /*  cout << nowpos << " " << pos << endl; */
        }
        pos = nowpos;
        dist.push_back(nowpos);
    }
    sort(dist.begin(), dist.end());
    dist.erase(unique(dist.begin(), dist.end()), dist.end());
    /*  for (int i = 0; i <= dist.size() - 1; i++)
         cout << dist[i] << " ";
     cout << endl; */
    for (int i = 1; i <= n; i++)
    {
        int l = get(arr[i].first), r = get(arr[i].second);
        /* cout << l << " " << r << endl; */
        pre[l] += 1, pre[r] -= 1;
    }
    for (int i = 1; i <= dist.size() - 1; i++)
        sum[i] = sum[i - 1] + pre[i];
    int ans = 0;
    for (int i = 1; i < dist.size() - 1; i++)
    {
        if (sum[i] >= 2)
            ans += dist[i + 1] - dist[i];
    }
    cout << ans;
    return 0;
}

 《逆向思维的差分》

 这道题要我们找出温度，但是我们不如逆向考虑一下，

对于每一头牛，给定区间[l，r];我们不如首先来一个温度轴

每一头牛，在温度[0,l-1]上产奶x，[r+1,INF]上产奶z,【l,r】上产奶y，然后可以将这些值加入到温度轴上

在全部牛枚举完后，扫一遍温度轴上的数值，然后最大值对应的温度即为答案

但是温度轴有0-1e9，但是牛有20000比较小，说明温度值出现的全部值不超过40000，用离散化

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 4 * 1e4 + 5;
int n, x, y, z;
vector<int> temp;
pair<int, int> cows[N];
int pre[N];
int get(int x)
{
    int l = 0, r = temp.size() - 1, ans = -1;
    while (l <= r)
    {
        int mid = (l + r) >> 1;
        if (temp[mid] >= x)
        {
            ans = mid;
            r = mid - 1;
        }
        else
            l = mid + 1;
    }
    return ans;
}
int main()
{
    cin >> n >> x >> y >> z;
    for (int i = 1; i <= n; i++)
    {
        int l, r;
        scanf("%d%d", &l, &r);
        cows[i] = {l, r};
        temp.push_back(l), temp.push_back(r);
    }
    temp.push_back(-1), temp.push_back(1e9 + 10);
    sort(temp.begin(), temp.end());
    temp.erase(unique(temp.begin(), temp.end()), temp.end());
    for (int i = 1; i <= n; i++)
    {
        int l = get(cows[i].first), r = get(cows[i].second);
        pre[0] += x;
        pre[l] += y - x;
        pre[r + 1] += z - y;
    }
    int ans = 0, num = 0;
    for (int i = 0; i <= temp.size() - 1; i++)
    {
        num += pre[i];
        ans = max(ans, num);
    }
    cout << ans;
    return 0;
}