dp----在一些意想不到的地方用到了dp

《题一:Subsequence Path》

原题链接:https://atcoder.jp/contests/abc271/tasks/abc271_e

原题详细题解：https://atcoder.jp/contests/abc271/editorial/4940

题目大意:

有N个城镇编号为1、…、N和M，道路编号为1…、M。

给定一个长度为K的序列E，由1到M之间的整数组成。使用道路从城镇1到城镇N的旅行方式称为好路径，如果：

按照路径中使用的顺序排列的道路编号序列是E的子序列。

请注意，序列的子序列是通过从原始序列中删除0个或多个元素，并在不更改顺序的情况下连接其余元素而获得的序列。

找出一条好路中所用道路的最小长度总和。

如果没有好的道路，请报告这一事实。

 

 我的思想思路:

首先我在想各种图论中的算法，但是失败

然后我想对E这个序列作手脚，但是最后我只能够想到对这个序列爆搜，对于序列上的每一个点看是否要选，然后能否到最终点

但是时间复杂度肯定会超时

然后我就没有想到dp

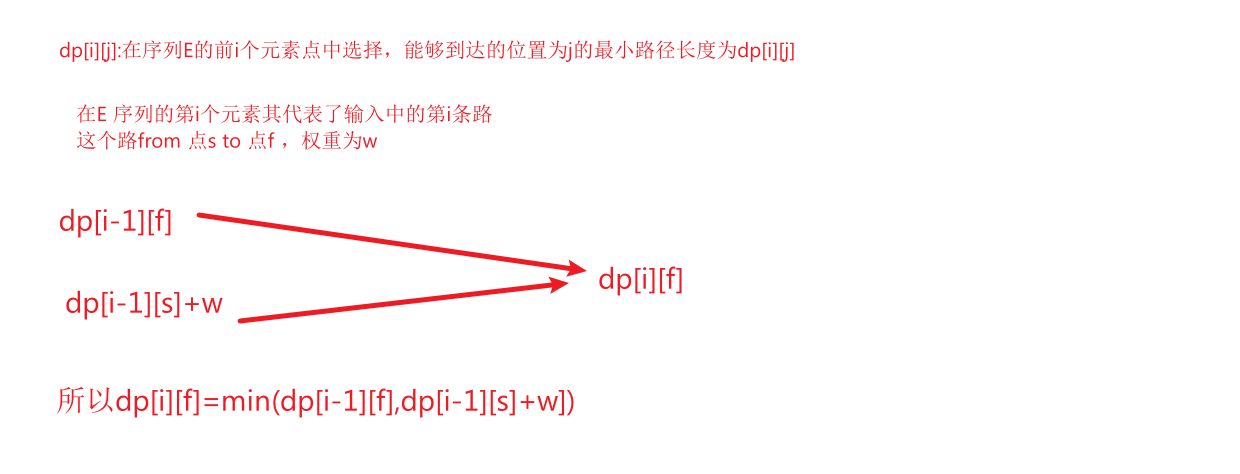
这里用dp的话dp状态转移方程十分好些：

 

 

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 2 * 1e5 + 5;
const long long INF = 1e18;
int n, m, k;
PII roads[N];
int len[N];
long long dp[N];
int main()
{
    cin >> n >> m >> k;
    for (int i = 1; i <= m; i++)
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        roads[i] = {a, b};
        len[i] = w;
    }
    for (int i = 0; i <= n; i++)
        dp[i] = INF;
    dp[1] = 0;
    while (k--)
    {
        int index;
        scanf("%d", &index);
        int s = roads[index].first;
        int f = roads[index].second;
        int w = len[index];
        if (dp[f] > dp[s] + w)
            dp[f] = dp[s] + w;
    }
    if (dp[n] >= INF)
        cout << -1;
    else
        cout << dp[n];
    return 0;
}